基于前景理论的犹豫模糊语言绿色供应商优选决策

施明华，肖庆宪

（1.上海理工大学 管理学院，上海 200093；2.皖西学院 金融与数学学院，安徽 六安 237012）

0 引言

采购环节中选择好绿色供应商，在整个绿色供应链中占有重要地位，并能将环境保护上的作用传递到链条中的其他环节。鉴于此，很多学者对绿色供应链中的供应商选择进行研究，并提出一些决策方法[1-5]。但模糊语言其本身并不完善，例如当决策专家受限于自身知识或时间等因素时，往往会在几个评价术语值之间犹豫不决，此时传统的模糊语言理论无法进行决策建模。为解决这一问题，Rodriguez等[6]2012年在犹豫集和模糊语言术语集的基础上，进一步提出犹豫模糊语言术语集。为处理模糊不确定环境下的决策问题提供一种新的途径，能更好的保留专家在决策过程中的评价信息，目前已被广泛应用于解决多个管理领域的决策问题。但这些决策方法存在以下问题：一是大多采用集结算子通过“词计算”完成决策信息集结，这中间需要扩充犹豫模糊语言术语元素的维度，会使得决策信息发生丢失和扭曲现象；二是在决策者完全理性的假设下，采用TOPSIS、PROMETHEE以及VIKOR等算法进行优先决策，这会导致决策结果可信度不高。三是这些决策研究中没有涉及用犹豫模糊语言处理供应链中的绿色供应商选择问题。

鉴于上述分析，本文提出一种新的犹豫模糊语言供应商多属性决策方法。

1 预备知识

1.1 前景理论

实验显示不确定风险环境下，人类的决策行为常和期

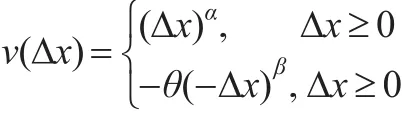
其中Δx为决策结果相对于心理预期参照点的收益或者损失，若Δx≥0则表示获得收益，此时价值函数是凹函数；Δx＜0则表示产生损失，此时价值函数是凸函数。换句话说，即面对收益时，人们表现出风险规避，而在损失情形下表现出追求风险的特征。参变量α和β分别表示价值函数的凹凸程度，θ用来刻画损失区域的凸函数比收益区的凹函数更加陡峭。Kahneman等通过大量的实验，给出了参数的理想设置，即α=β=0.88，θ=2.25。

1.2 犹豫模糊语言

出于人类思维的本能以及数据信息获取成本过高等因素，人们在决策过程中往往会选择定性的方式对事物进行评价，规范化的术语集是一种常用的方式。设S={sα|α=1，2，…，t}是模糊语言术语集，sα为可能的语言评价值，并满足条件：①sα＜sβ⇔α＜β;②互反N(sβ)=sα，αβ=1。

例如评价工业流程的复杂性时，可建立术语集：

S={s1:非常复杂,s2:稍复杂,s3:有点复杂,s4:一般,s5:有点简单,s6:稍简单,s7:非常简单}

但这种离散形式的术语集不便于决策建模，徐泽水进一步提出连续模糊语言术语集ˉ={sα|α∈[0，M]}，其中M为充分大的正整数。设sα,sβ∈，λ∈[0，1]，规定如下运算法则[7]：望效用理论相背离。为此，行为经济学家Kahneman等提出前景理论，由于其在构建决策偏好框架的优势，理论一经提出便引起众多学者的关注，并产生丰硕的研究成果。

价值函数是前景理论的核心内容，是描述并度量决策者的心理行为的有效工具，数学形式为：

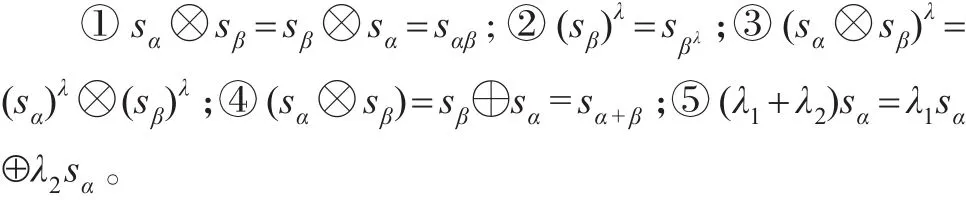
为解决传统模糊语言术语集无法对专家在几个评价值间犹豫时进行决策建模的问题，Rodriguez等进一步提出了犹豫模糊语言术语集这一概念。

定义1[8]：设X={1，2，…，N}为正整数集，S={sβ|β=1，2，…，τ}为语言标度集。称HS为论域X上的犹豫模糊语言术语集（HFLTS）。

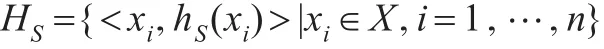
其中hS(xi)为S中元素构成的集合，称为犹豫模糊语言元素（HFLE）。hS(xi)={sϕl(xi)|sϕl(xi)∈S，l=1，2，…，L}，L表示hS(xi)中元素个数。

定义 2[9]：设S={sβ|β=1，2，…，τ}为语言标度集，hS={sηl|sηl∈S，l=1，2，…，L}是定义在S上的HFLE。hS的均值与方差分别定义为：

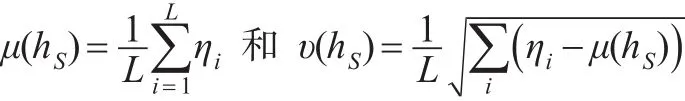
2 犹豫模糊语言Hausdorff距离测度

目前文献中常用的犹豫模糊语言距离测度公式有：汉明距离、欧式距离等。这些公式在使用中，均需要HFLE中的语言术语个数相同。若条件不满足，则对个数少的集合添加元素，直到二者具有相同元素，其中0≤β≤1表示为hS(x)中的最大和最小术语。但这种方式容易引起决策信息的扭曲，选取不同的β会产生不一样的距离值。例如利用文献[8]所定义的汉明距离，计算7标度集S下的犹豫模糊语言元素和的距离。若将拓展为，则；若将拓展为则若 将拓 展 为，则。可见这种计算方式过于随意，主观性太

强，更重要的是改变了原始信息，容易引起决策信息扭曲。

对于维数不相同的数据样本，Knauera定义了Hausdorff距离测度公式[10]。设X={x1，x2，…，xn} 和Y={y1，y2，…，ym}是2个数据集，记||.||为欧几里得度量，则X和Y之间的Hausdorff距离为。但d(X，Y)只能度量离散数据间的距离，对于离散语言术语集则无法计算，并且不具有对称性。为此，本文对Hausdorff距离测度公式进行改造，并给出一种广义的犹豫模糊语言Hausdorff距离测度。

定义3：设为语言标度集,则S上的任意两个犹豫模糊语言元素的广义 Hausdorff距离为(0＜λ)：

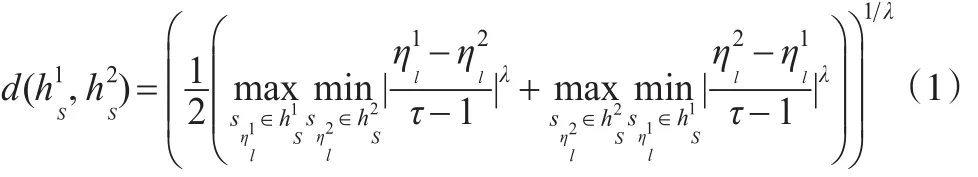
注：（1）若λ=1，则（1）退化为犹豫模糊语言Hamming-Hausdorff距离:

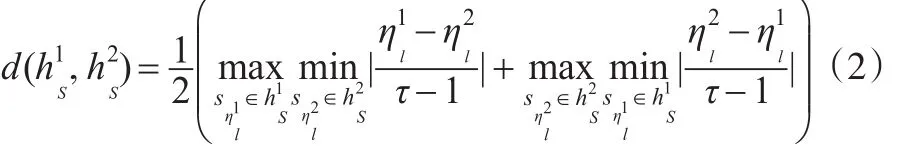
（2）若λ=2，则（1）退化为犹豫模糊语言Euclidean-Hausdorff距离:

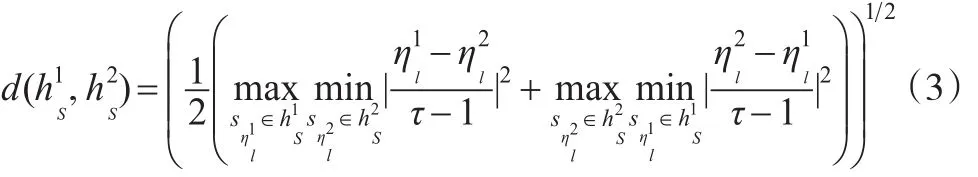
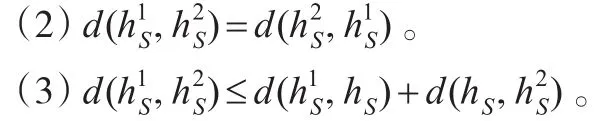
即：

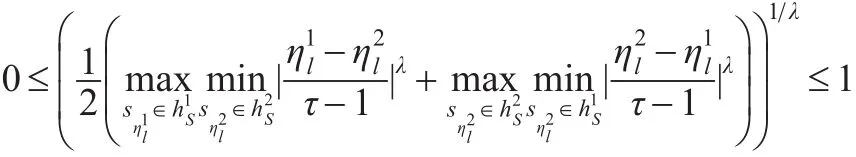
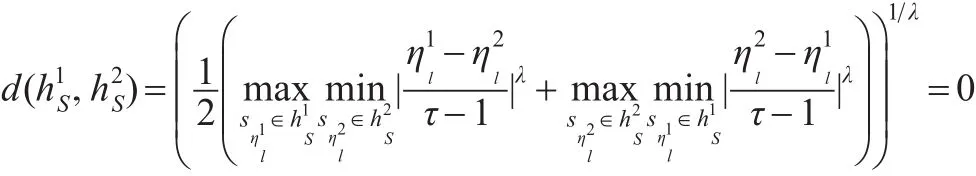
当和中的语言术语分别为s1和sτ时，这里不妨假设有：

3 多属性决策方法

3.1 问题描述

对于犹豫模糊语言环境下的绿色供应商选择决策问题，首先给出语言术语集，本文统一采用九标度描述评价信息，具体为：S={s1:极差,s2:很差,s3:差,s4:有点差,s5:一般，s6:有点好,s7:好,s8:很好,s9:极好}。

设有n个供应商X={x1，x2，…，xn}可供选择，企业根据自身的特点制定经济社会方面的评价指标集G={g1，g2，…，gm} ，相 应 的 属 性 权 重 为w=(w1，w2，…，决策专家对供应商提供犹豫模糊语言评价信息，并构建出犹豫模糊语言评价矩H=(hij)n×m，其中hij代表供应商xi在指标gj的评价值。

3.2 方法步骤

正如文献[11]所阐述，大多数基于算子的犹豫模糊语言决策方法，均需要对专家提供的评价数据集进行拓展保证元素集维度相同，这会导致决策信息的扭曲。因而很多学者采用优先关系为基础的算法，诸如：TOPSIS、VIKOR、ELECTRE等，但这些方法无一例外以决策者外完全理性为前提，忽略了决策者的行为效用。为此本文基于前景理论和PROMETHEE方法，给出一种新的决策模型。

步骤1：构建加犹豫模糊语言规范化决策矩阵。利用Liao等[9]所给出的方法，将决策矩阵转化为规范化矩阵

步骤2：计算候选变量的价值矩阵。

对候选变量xi分别构建收益矩阵，其中，以及损失矩阵其中采用前文所定义的Hamming-Hausdorff距离，参数设置为

步骤4：分别计算候选方案的xi的相对价值优度ϕ+(xi)和相对价值劣度ϕ-(xi)，其中

步骤5：分别计算候选方案的xi的绝对价值优度ϕ(xi)=ϕ+(xi)-ϕ-(xi)，i=1，2，…，n，并依据ϕ(xi)对候选方案进行排序，ϕ(xi)越大表示方案xi越优。

4 实例分析

某品牌手机公司有5个可供选择的电池货源，为选择出最佳绿色供应商，该公司制定了4个评价指标(相应权重为w=(0.15，0.3，0.2，0.35)：创新能力(g1)、使用环境友好型的材料与生产技术(g2)、服务水平(g3)、产品质量与价格(g4)；决策专家按上述指标集对5家供应商进行评价，并给出如下的决策矩阵（见表1）。

表1 决策矩阵

4.1 方法求解

步骤1:构建加犹豫模糊语言规范化决策矩阵。本例中的属性均是收益型的，因此不需对决策矩阵进行规范化，即

步骤2：计算候选变量的价值矩阵，这里以第三家候选公司x3为例，有：

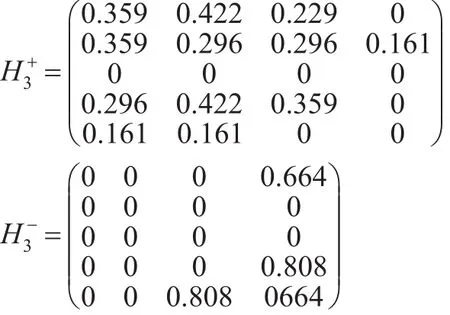
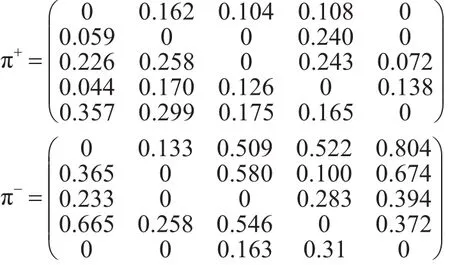
步骤4：计算候选方案的相对价值优度ϕ+(xi)和相对价值劣度ϕ-(xi)。

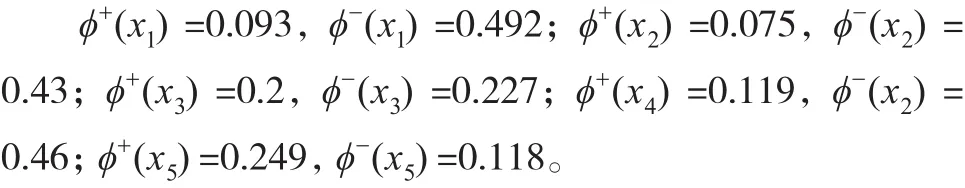
步骤5：计算候选方案的xi的绝对价值优度。

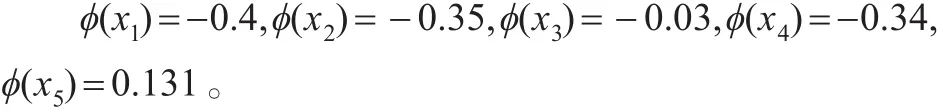
由此可得候选方案的排序为x1≺x2≺x4≺x3≺x5，最佳合作伙伴为x5。

4.2 对比分析

在文献中已有的犹豫模糊语言信息集结算子中，有针对性的选取文献[11-13]给出的方法同本文的方法进行对比（见表2）。

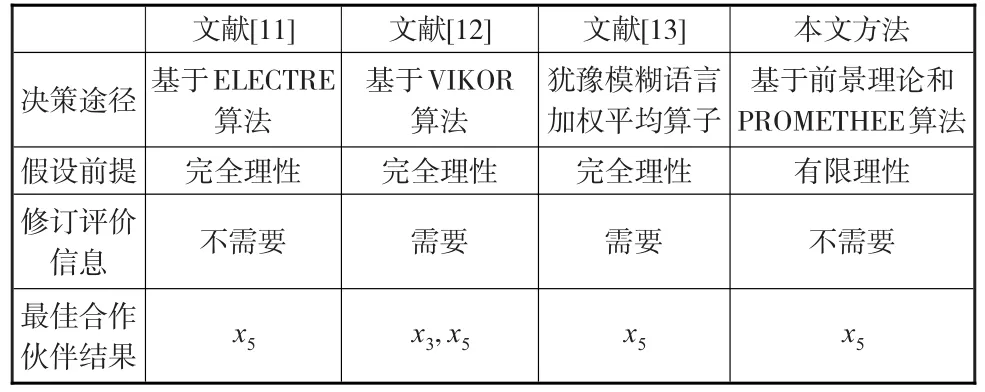
表2 方法比对结果

文献[12]无法给出最优解，只能给出折中的妥协解，这是因为文献[12，13]需要对原始评价信息进行修订，确保评价变量具有相同的维度，容易发生信息扭曲。而其他两种方法直接对原始信息进行处理，但本文的方法充分考虑了决策者的行为因素，在前景理论基础上对传统的PROMETHEE方法进行设计，因而计算结果更为可靠。但任何一种方法都不可能在一切情形下占有优势，方法都有优缺点。例如文献[13]的方法尽管易导致信息扭曲，但计算简洁、效率高。本文所要做的是针对不同的决策环境和决策问题，选择合理的决策方法。

5 结束语

选择最优绿色供应商是整个绿色供应链中的重要环节，鉴于人类思维的模糊性和决策信息的不确定性，本文在文献[3-5]所给出的模糊语言绿色供应商决策方法基础上，提出一种犹豫模糊语言决策方法。为此，提出一种新的犹豫模糊语言距离测度公式，并结合前景理论与PROMETHEE方法，提出一种有限理性下的绿色供应商选择方法。本文给出的属性权重是决策专家依据先验经验直接赋予的，下一步的研究工作是尝试给出一种客观赋权法的犹豫模糊语言绿色供应商决策方法，同时尝试利用本文的方法解决其他企业管理中的决策问题。