一种新的基于群AHP和DEA的距离测度方法

范建平，朱兆钰，吴美琴

（山西大学 经济与管理学院，太原 030006）

0 引言

属性权重的大小对于方案的评价结果具有很大程度的影响，是多准则决策问题中一个重要问题[1]。目前求解权重的方法可以主要分为主观赋权法、客观赋权法和组合赋权法。主观赋权法是由决策者或专家根据自身的知识、经验以及对决策问题的理解和判断而直接给出偏好信息的方法，比如层次分析法（AHP）[2，3]、专家调查法（Delphi法）[4]、偏好比率法[5]等。客观赋权法主要根据原始数据之间的关系由数据驱动来确定权重，比如主成分分析法[6]、熵值法[7]、数据包络分析法[8，9]等。组合赋权法则是通过线性加权等方式将主客观权重进行集结得出一个综合权重的方法，该方法能够给出更为合理的指标权重。其中诸多学者[10，11]通过将AHP方法和DEA方法相结合来获得综合权重，但是在这些研究中使用AHP方法来获得主观权重时仅考虑一位专家的判断，这不利于对指标重要性的全面衡量。而在使用DEA方法确定客观权重时通常采用原始CCR模型，该模型所求得的指标权重会存在权重不唯一的问题，这时通过该模型得出的客观权重是最有利于评价单元自身的权重，使用该权重来进行评价并无法体现严格意义上的客观性。

本文提出一种基于群AHP和DEA的闵式距离测度方法，该方法以闵式距离测度为中心模型，通过群AHP方法以及借鉴相对贴近度思想对多位专家的主观判断进行集结得到更为全面的主观权重，通过能够获得公共权重的DEA方法来获得客观权重，从而确定各方案更为合理的综合权重向量，进而计算得出各备选方案与理想方案之间的距离，根据计算得出的距离远近来进行决策。这一方法综合了群AHP、DEA和距离测度三种方法的优势，使得该方法可以应用于更广泛的评价、排序场合当中。最后通过一个国家可持续发展实验区创新能力评价的实例来验证该方法的有效性和可行性。

1 基于群AHP和DEA的综合权重确定

1.1 基于群AHP的指标权重计算

群AHP是一种定性与定量分析相结合的多准则决策方法，其基本思想是把决策问题的有关元素按照支配关系形成层次结构，用一定标度对多位专家的主观判断进行客观量化，构造出多个判断矩阵，并在此基础上计算各指标的权重系数，再将多位专家给出的权重系数进行集结得出最终的各指标权重系数。具体步骤如下：

（1）构造各位专家的判断矩阵

判断矩阵表示针对上一层次因素，本层次与之相关的因素之间相对重要性的比较。为了使决策判断定量化，本文采用Saaty提出的1-9标度法。

（2）计算各位专家的指标权重值

计算判断矩阵的最大特征值及其对应的特征向量，最大特征值所对应的最大特征向量即为各元素的权重。

（3）各位专家矩阵的一致性检验

①计算一致性指标CI

②查找相应的平均随机一致性指标R.I.

对于1-9阶判断矩阵，该值可通过查表1得出。

表1 平均随机一致性指标RI

③计算一致性比率C.R.

当CR＜0.1时，即认为判断矩阵具有满意的一致性，否则需要对判断矩阵进行调整。

（4）各位专家的指标权重值集结

设邀请m位专家对具有n个指标的备选方案进行评估，将通过上述步骤得出的第i位专家评价的指标权重记为Wi=(wi1，wi2，...，win)(i=1，2，...，m)。在决策问题中，多位专家对决策问题进行决策时应遵循一致性最大化原则，因此对各位专家的重要性判断则借鉴相对贴近度的思想，通过每位专家给出的指标权重之间的相对相似性程度来对专家的重要性进行判断，而每位专家给出的指标权重之间的相似程度则通过欧氏距离来测量。

专家i与专家j通过AHP方法分别得出的指标权重分别为Wi=(wi1，wi2，...，win)，Wj=(wj1，wj2，...，wjn)(i≠j)，则 i和j两位专家所给出的指标权重之间的相似度dij为：

在计算得出专家i给出的指标权重和其余m-1位专家所给出的指标权重之间的相似度后，选出专家i的指标权重与其余m-1位专家的指标权重之间最高和最低的相似度，分别记为，则专家i与其余专家的相对相似程度ci为：

通过将专家i给出的主观权重的相对相似程度ci(i=1，2，...，m)进行归一化，可得专家i的重要性程度vi为：

由此可得出各专家的权重值V=(v1，v2，...，vm)，则集结后的主观指标权重为W1=(W1，W2，...Wm)×VT。

1.2 基于DEA的指标权重计算

由于通过DEA方法求解得出的客观权重与通过AHP方法求解得出的主观权重相比可能会出现数值过小的情况，这会削弱客观权重的作用，因此在运用DEA方法求解客观权重之前首先需要将指标数据进行无量纲化处理。本文用式（6）将决策矩阵中的X=(xij)m×n无量纲化成相应的元素rij。

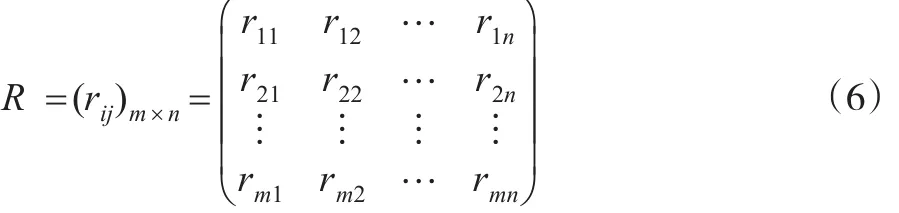
其中，对于效益型指标来说：

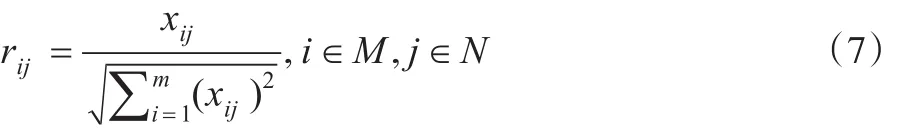
对于成本型指标来说：

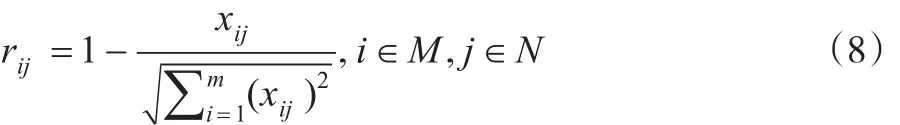
在对指标数据进行无量纲化后，接着运用DEA方法来求解客观权重。运用DEA方法求解客观权重所使用的是熊文涛等[12]所提出的基于理想决策单元确定公共权重的方法。假定有m个决策单元DMUi（i=1,2,…,m），n个评价指标，其中每个决策单元都有p种类型的输入和q种类型的输出，对应的输入向量为Xi=(x1i，x2i，...，xsi，...，xpi)T，输出向量为Yi=(y1i，y2i，...，yti，...，yqi)T，并且p+q=n，xsi＞0(s=1，2，...，p)，yti＞0(t=1，2，...，q)。同时，引入输入权重向量V=(v1，v2，...，vs，...，vp)T，输出权重向量U=(u1，u2，...，ut，...，uq)T。

1.2.1 效率下界的确定模型

通过公共权重，将所有DMUs的效率综合在一起，得到下述的多目标分式规划（MOFP）模型：

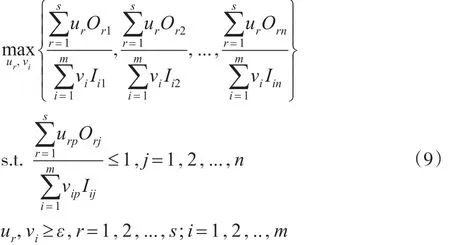
其中，ur，vi是所有DMUs的公共权重。

为了求解上述MOFP问题，引入非负变量α，将其作为每个DMU的效率下界，即，效率下界α越大越好。上述的多目标分式规划可以进一步转换为如下的非线性规划模型：

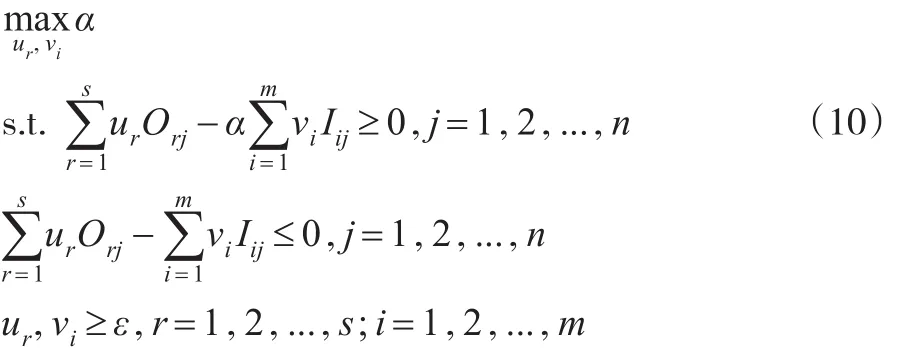
在模型（10）中 ，对于所 有DMUs来 说均会随α的增加而不断减少，当α增加到 某 个值α*时...，n将不会全部满足，这时α*为模型（10）的全局最优解。为了计算α*，设，可构造如下的非线性规划模型（11）：

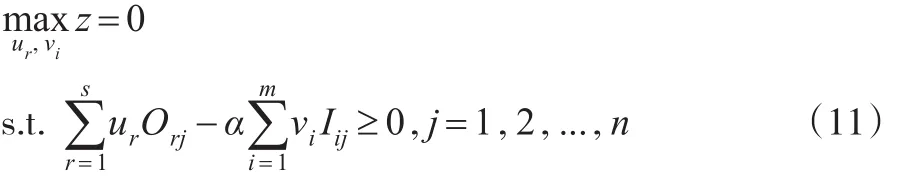
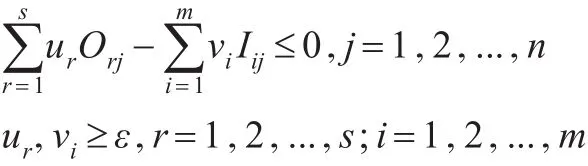
求解α*时采用二分法求解，具体步骤如下：

输入：数据Iij，Orj，初始左端点a=0，右端点b=1，精度η。

输出：所有DMUs的效率下界值α*。

第二步：令a=α*，若|b-a|≤η，则输出α*；否则，转第一步；

第三步：令b=α*，若|b-a|≤η，则令α*=a，输出α*；否则转第一步。

1.2.2 基于理想决策单元的公共权重的确定模型

当计算出所有DMUs的效率下界后，将α*带入模型（11），得到一些线性约束条件。为了得到唯一的公共权重集，选取虚拟的理想决策单元作为参考对象来作为评价标准。假设有n个DMUs，每个DMUj（j=1，2，...，n）具有m个不同的投入Ij=(I1j，I2j，...，Imj)T，s个不同的产出Oj=(O1j，O2j，...，Osj)T。对于投入指标来说，选取所有DMUs中最小的数据作为理想决策单元（IDMU）相应的投入；对于产出指标来说，选取所有DMUs中最大的数据作为IDMU相应的产出。即

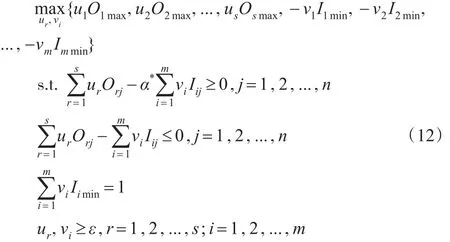
对于理想决策单元，总是希望以最小的投入得到最大的产出。可构建如下的多目标线性规划模型：

其中α*为上文通过二分法得到的下界值。对于多目标规划模型（12）采用分层序列法求解。求解得出的客观权重为

1.3 综合权重的计算

群AHP方法反映出多位评价者的主观偏好，DEA方法反映了数据所包含的客观信息，为了充分体现AHP方法和DEA方法的优点，本文将群AHP方法和DEA方法进行整合，采用线性加权的方法来共同确定评价指标的综合权重。这种方法比单一的AHP方法或DEA方法更具有准确性和客观性，具体计算公式如下：

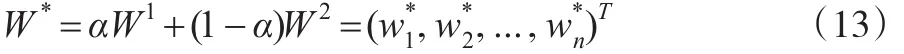
式中，W*为求得的综合权重，α为主观偏好系数，1-α为客观偏好系数，α∈[0，1]。当面临的决策问题或决策环境是基本确定的时，α的取值范围为[0，0.5) ；当面临的决策问题或决策环境存在风险时，α取值为0.5；当面临的决策问题或决策环境具有高度不确定性时，α的取值范围为(0.5，1]。

2 基于群AHP和DEA的闵式距离测度模型

距离测度是决策领域中一种有效的评价方法，在决策中使用距离测度的主要优势是可以将备选方案与理想方案进行比较[13]，根据备选方案与理想方案之间的距离来最终确定最优方案，并且在评价过程中可以了解备选方案与最优方案之间各指标的差距，从而可以根据评价结果为决策者提出有效的对策和建议。在决策中使用的距离测度有不同的距离表达式形式[13，14]，比如海明距离、欧几里德距离、闵可夫斯基距离。Merigó和Casanovas[14]指出闵可夫斯基距离是概括了包括海明距离、欧几里德距离在内的一种距离测度，其通过使用诱导有序加权平均算子提出一个闵可夫斯基距离的一般形式。随后，Casanovas等[15]将诱导闵可夫斯基有序加权平均距离算子应用到模糊环境中的再保险项目中。而Xian等[16]则将诱导有序加权闵可夫斯基距离算子扩展到模糊环境下，通过定义一个模糊语言变量距离提出了一个称为模糊语言诱导有序加权闵可夫斯基距离算子的新算子，并且给出这一算子所具有的主要性质。但是在这些文献中并未给出具体指标权重的获取方法。

假定系统由m个方案和n个指标构成，则第i个方案的 n 个指标值构成数列Ai=(ai1，ai2，...，aij，...，ain)(i=1，2，...，m;j=1，2，...，n)，那么m个方案的原始指标值构成如下矩阵A：

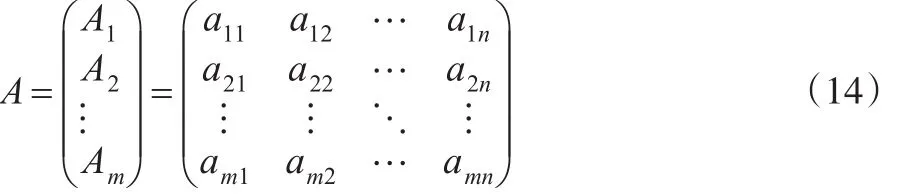
2.1 确定最优方案指标集

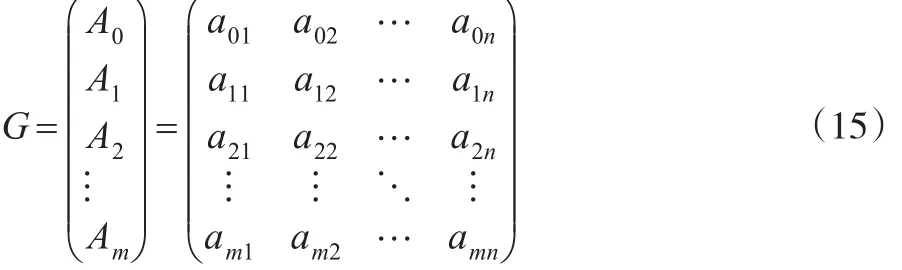
2.2 指标值的规范化处理

在上文运用DEA方法求解客观权重时已经对数据进行过无量纲化处理，在这里则设按照式（3）、式（5）对数据处理后得到的规范化矩阵为H:

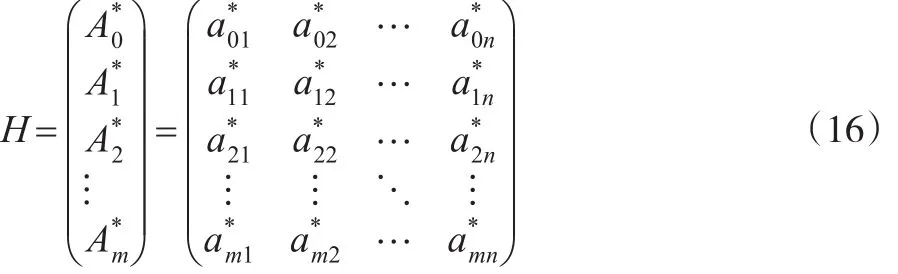
2.3 方案集与最优指标集的距离确定

根据指标权重向量W*，可求得各方案集与最优指标集的闵式距离[4]：

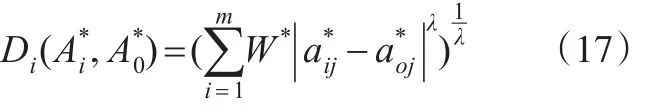
距离Di越小，说明方案集与最优指标集越接近，即方案集越优，因此可根据距离的大小来对方案进行优劣排序。

因此，本文提出的基于群AHP和DEA的多准则决策方法的步骤如下：

第一步：邀请多位专家通过对指标两两进行比较来对指标的重要性进行打分，通过群AHP方法以及借鉴相对贴近度的思想对多位专家所给出的主观权重集结得出指标的主观权重；

第二步：运用决策问题中的客观数据，通过基于理想决策单元的DEA方法求解得出指标的客观权重；

第三步：根据具体决策问题，遵循文中所给出的原则，确定主观偏好系数α的值，进而将主客观权重线性加权得出综合权重；

第四步：通过加权闵式距离测度来对决策单元进行评价，并根据评价结果作出决策。

3 数值分析

3.1 指标体系

本文对中部六省八个城区型国家可持续发展实验区创新能力进行评价，其评价指标体系见表2。

表2 国家可持续发展实验区创新能力评价指标体系

3.2 基于群AHP的指标权重计算

邀请三位专家根据已确定的指标集，通过将指标两两进行比较得出判断矩阵，经计算得出三位专家给出的指标权重分别为：W1=(0.2123，0.1131，0.0991，0.2330，0.1563，0.1036，0.0826)T，W2=(0.1203，0.1180，0.0369，0.2187，0.0508，0.1932，0.2620)T，W3=(0.1523，0.0499，0.1857，0.0265，0.0560，0.2898，0.2380)T。三位专家的权重为：V=(0.3148，0.3562，0.3290)，将三位专家得出的指标权重进行集结，得到AHP的 综 合 权 重 为 ：W1=(0.1598，0.0941，0.1054，0.1600，0.0857，0.1968，0.1976)T

3.3 基于DEA的指标权重计算

将取值越小越好的成本型指标作为输入指标，将取值越大越好的效益型指标作为输出指标。在建模之前首先对指标的原始数据进行无量纲化处理，通过式（6），将每个实验区的原始指标值无量纲化见表3。

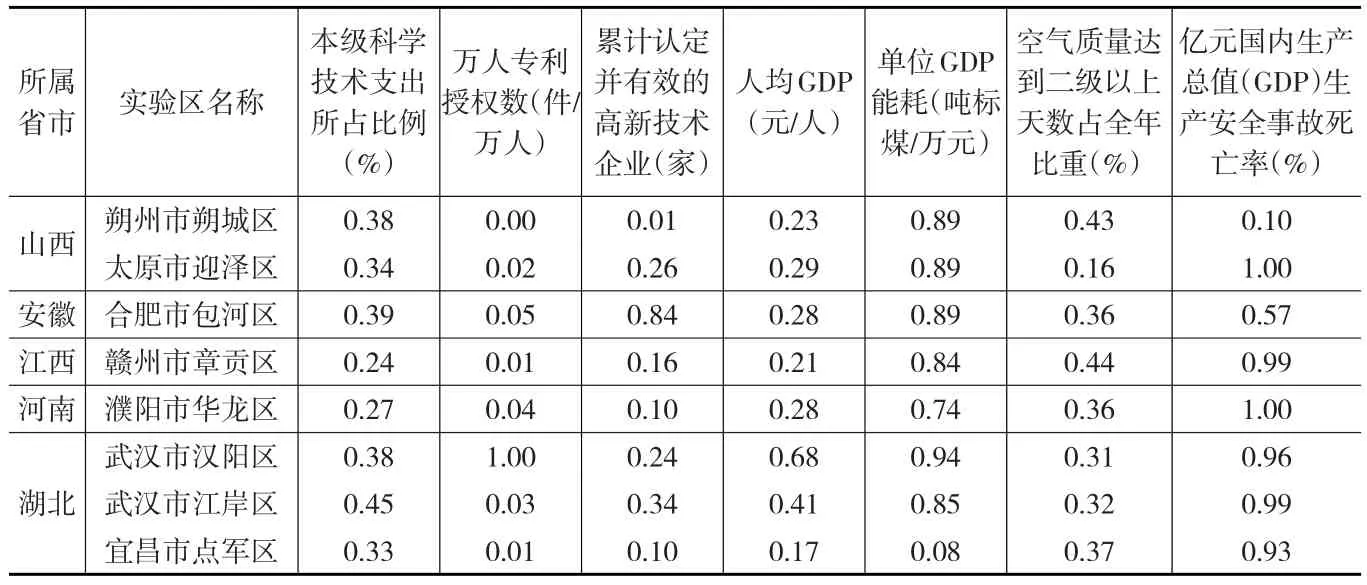
表3 中部六省城区型国家可持续发展实验区创新能力规范化评价矩阵

本文运用Matlab编程软件可求得客观权重为：W2=(0.0781，0.0523，0.1461，0.1788，0.1895，0.1334，0.2218)T

3.4 综合权重的计算

由于该评价环境较为确定，因此本文取主观偏好系数α=0.2，根据上文给出的计算公式可得综合权重为：W*=(0.0944,0.0607,0.1380,0.1750,0.1687,0.1461,0.2170)T3.5 基于群AHP和DEA的闵式距离测度模型

本文选取λ=1，根据式（17）可得各评价方案与最优指标集的距离Di(i=1，2，…，m)，根据距离Di的大小可对各实验区的创新能力进行排名，即距离Di越小则该实验区创新能力越高，具体结果见表4。

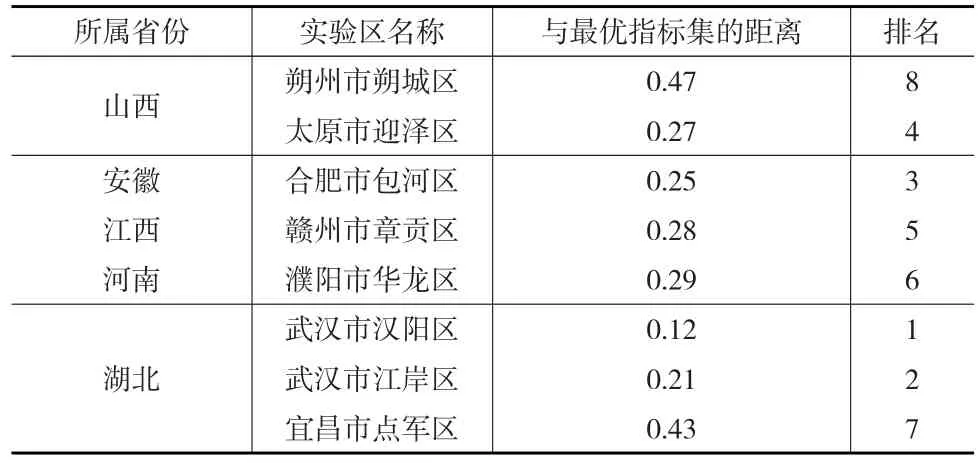
表4 中部六省城区型国家可持续发展实验区创新能力的距离及排名

根据文中方法得出的中部六省城区型国家可持续发展实验区的创新能力排名基本符合现实情况,由此证明了文中所提方法的有效性和可行性。

4 结束语

本文提出了一种新的基于群体AHP和公共权重DEA相结合的获取综合权重的闵式距离测度模型，通过使用群AHP方法以及借鉴相对贴近度的思想将多位专家给出的指标主观权重进行集结得出更为全面的主观权重，使用能够得出公共权重的DEA方法来确定更为客观和公平的客观权重，从而共同确定更为合理的评价指标的综合权重向量，其既能够反应多位专家的主观判断偏好同时也综合考虑了数据中所反映的客观情况，从而能够避免单独使用AHP方法的过于依赖专家的主观判断而造成的人为因素偏差以及单独使用DEA方法的运用数据驱动而造成的无法反映决策者主观偏好的问题。接着通过计算评价方案与最优方案之间的加权闵式距离来对方案进行排序，使用闵式距离测度可以提高该评价模型的适用范围，能够更好的适用于多种决策问题。该方法能够更好的兼顾权重获取过程中的主客观因素，从而能够增加决策过程的公平性和决策结果的可接受性。最后使用一个中部六省城区型国家可持续发展实验区的创新能力评价实例证明了该方法的有效性和可行性。本文所提方法能够对实验区创新能力评价提供一定的参考，并且该方法也可以应用于更广泛的评价、排序场合当中。