VSC-HVDC输电系统的模糊自抗扰控制

，,

(浙江工业大学 信息工程学院，浙江 杭州 310023)

高压直流输电技术分为汞弧阀换流时期、晶闸管换流阀时期以及新型半导体(IGBT)换流3个时期[1]。基于电压源型换流器的高压直流(Voltage source converter high voltage direct current, VSC-HVDC)输电技术的风电并网已被普遍认为是实现大型风机群并网的最稳定最有潜力的电能传输方式[2-3]。因为VSC-HVDC系统是一个多输入、多输出的耦合时变的非线性的系统，运行规则原理尤为复杂，只有通过选择合适的控制方法对换流器进行控制才能提高系统的性能。国内外学者在非线性控制方法、逆系统方法以及智能控制方法等方面做了大量卓有成效的工作[4]。刘凯等[5]推算出能够使交直流互联系统暂态能量不断下降的VSC-HVDC无功调制规律，设计模糊无功阻尼控制器，使得VSC-HVDC系统的调制容量得到提升。Tang等[6]针对VSC-HVDC系统的有功功率进行调制，并设计滑模控制器，显著抑制系统受干扰后的有功功率振荡问题。自抗扰控制[7](Active disturbance rejection control, ADRC)是韩京清研究员提出并不断完善的一种非线性控制方法。自抗扰控制技术是由跟踪微分器(Tracking differentiator, TD)、扩张状态观测器(Extended state observer, ESO)以及非线性状态误差反馈(Nonlinear states error feed-back, NLSEF)3部分构成。自抗扰控制器最主要的特点是把作用于被控对象的所有不确定因素影响都当作“未知扰动”，然后通过对象的输入输出数据对未知扰动进行估计并给与补偿。通过ESO环节观测出系统的综合扰动项，并对扰动项进行前馈补偿，从而实现被控对象的前馈线性化，因此系统的鲁棒性得到提升。目前，自抗扰控制技术已经在电力有源滤波器以及电力系统控制等方向得到应用，并取得了一些显著的成效。张善福[8]在送端系统和受端系统中设计内环自抗扰控制器，通过仿真证明ADRC控制器比PI控制器调节时间短，有更好的抑制超调的能力。董辉等[9]在永磁同步电机速度环中设计自抗扰控制器，有效抑制负载扰动对转速的影响。

针对VSC-HVDC输电系统，设计双闭环结构的控制器，其中内环采用ADRC控制技术与模糊控制相结合的方法设计模糊自抗扰控制器(Fuzzy active disturbance rejection controller, FADRC)，以此来增强系统的鲁棒性和抗干扰性；外环控制器采用PI控制方法。

1 两端VSC-HVDC的数学模型

图1为两端VSC-HVDC的系统结构图，其中L1，L2分别为换流变压器和电抗器的等效电感；R1，R2分别为换流变压器和电抗器的等效电阻；C1，C2分别为直流侧电容；Rd为直流输电线路的等效电阻；Ps1，Ps2和Qs1，Qs2分别为两侧交流电网向换流站流入的有功和无功功率；Idc为换流站流入直流端的电流；Id为直流端电流；udc为直流端电压；Pdc为直流端有功功率。

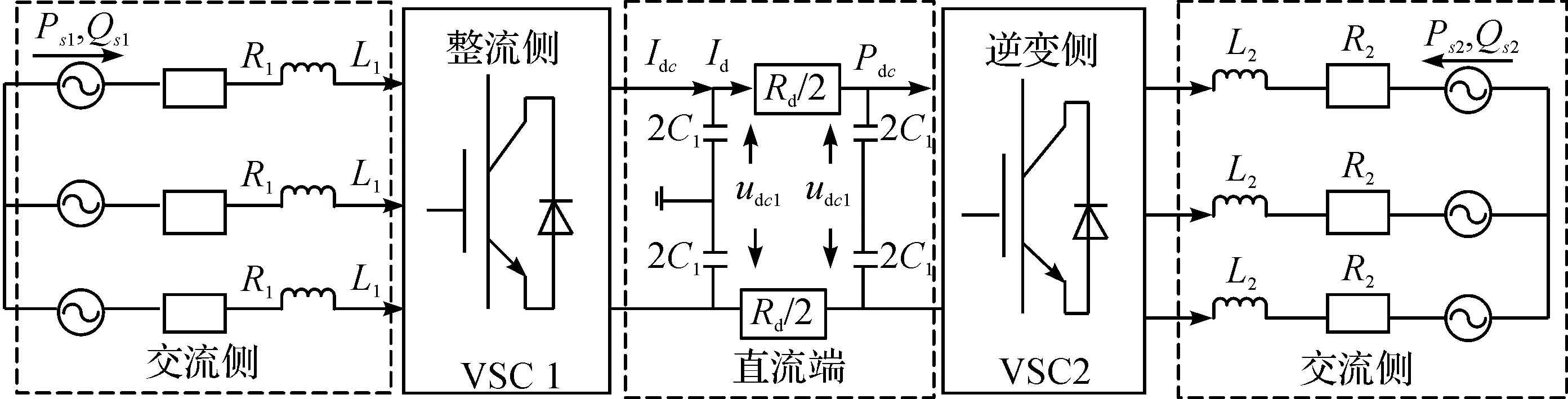
图1 两端VSC-HVDC系统结构图Fig.1 Block diagram for VSC-HVDC systems

VSC1为整流换流站，VSC2为逆变换流站。由于VSC-HVDC系统为两端对称结构，因此不失一般性，在此以整流侧VSC1为例进行分析，其具体结构如图2所示。

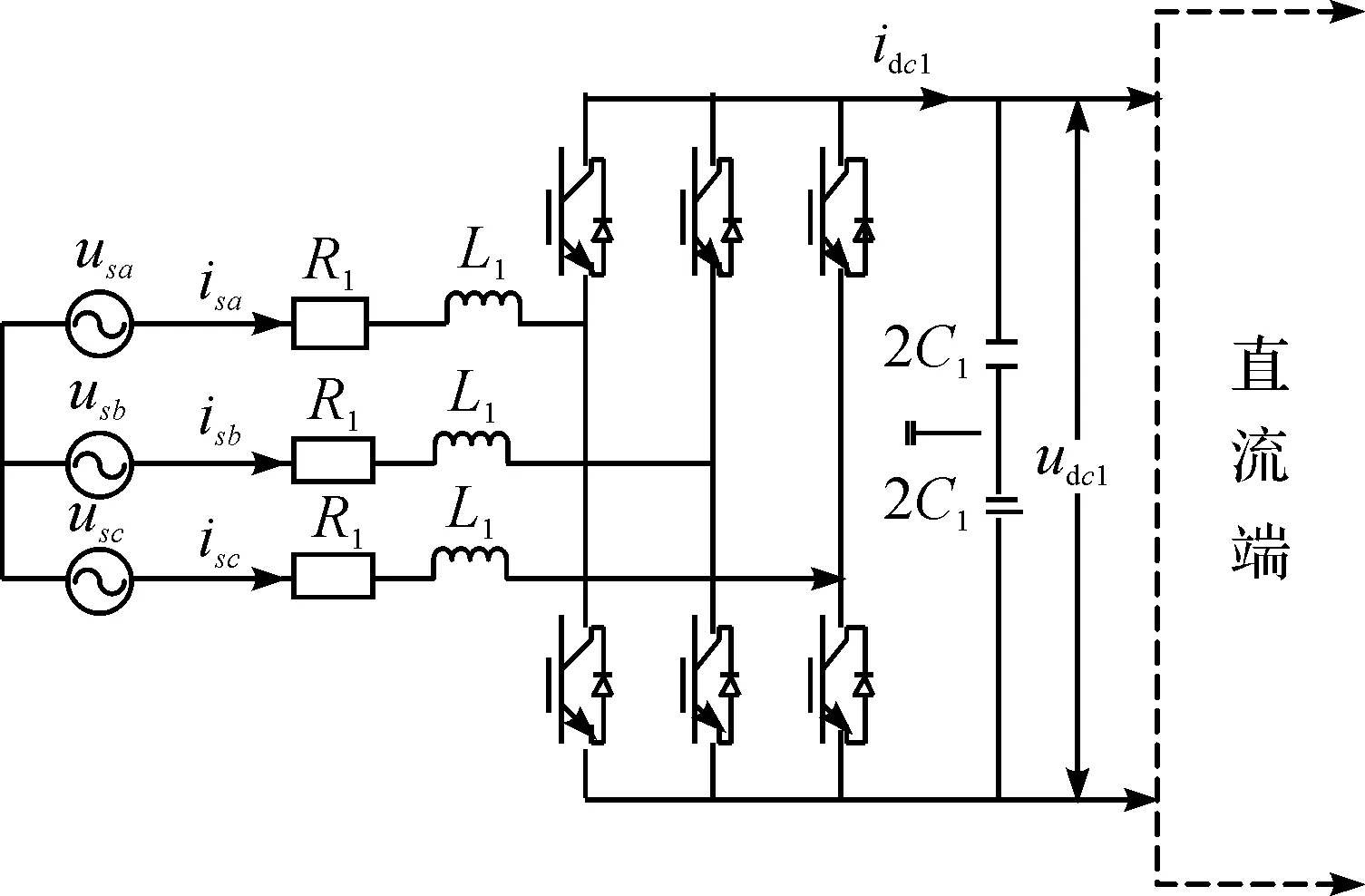
图2 电压源型换流器结构图Fig.2 Block diagram of the voltage source converter

根据图2的换流器结构图，将交流侧电流经Park变换后产生同步旋转坐标信号，可得电压平衡关系式[10]为

(1)

式中：usd，usq分别为交流源电压d和q轴分量；isd，isq分别为交流侧电流的d和q轴分量；ucd，ucq分别为换流站交流侧电压的d和q轴分量；ω为交流系统的角频率。通过式(1)可以看出：d轴和q轴电流之间存在耦合，并且会受到电网电压的影响。在电网三相平衡且对称运行时，交流侧功率表达式为

(2)

由式(2)可以看出：当交流侧连接无穷大系统时，电网电压基本上能保持稳定，所以d和q轴均能实现对功率的独立控制。直流端电流与有功功率表达式为

(3)

图3 双闭环VSC-HVDC原理图Fig.3 Schematic Diagram of dual closed-loop VSC-HVDC

2 内环模糊自抗扰控制器设计

以d轴为例，所设计的模糊自抗扰控制器如图4所示。模糊自抗扰控制器由自抗扰控制器和模糊控制两部分构成。

在实际中，ESO的参数常常是根据经验给定，面对不同的控制状态，需要手动调节参数的大小，因此引入模糊控制器。模糊环节可以将跟踪误差e0以及e0的微分信号e1作为模糊控制器的输入，通过对照模糊规则整定ESO的参数β1和β2，改善控制效果。

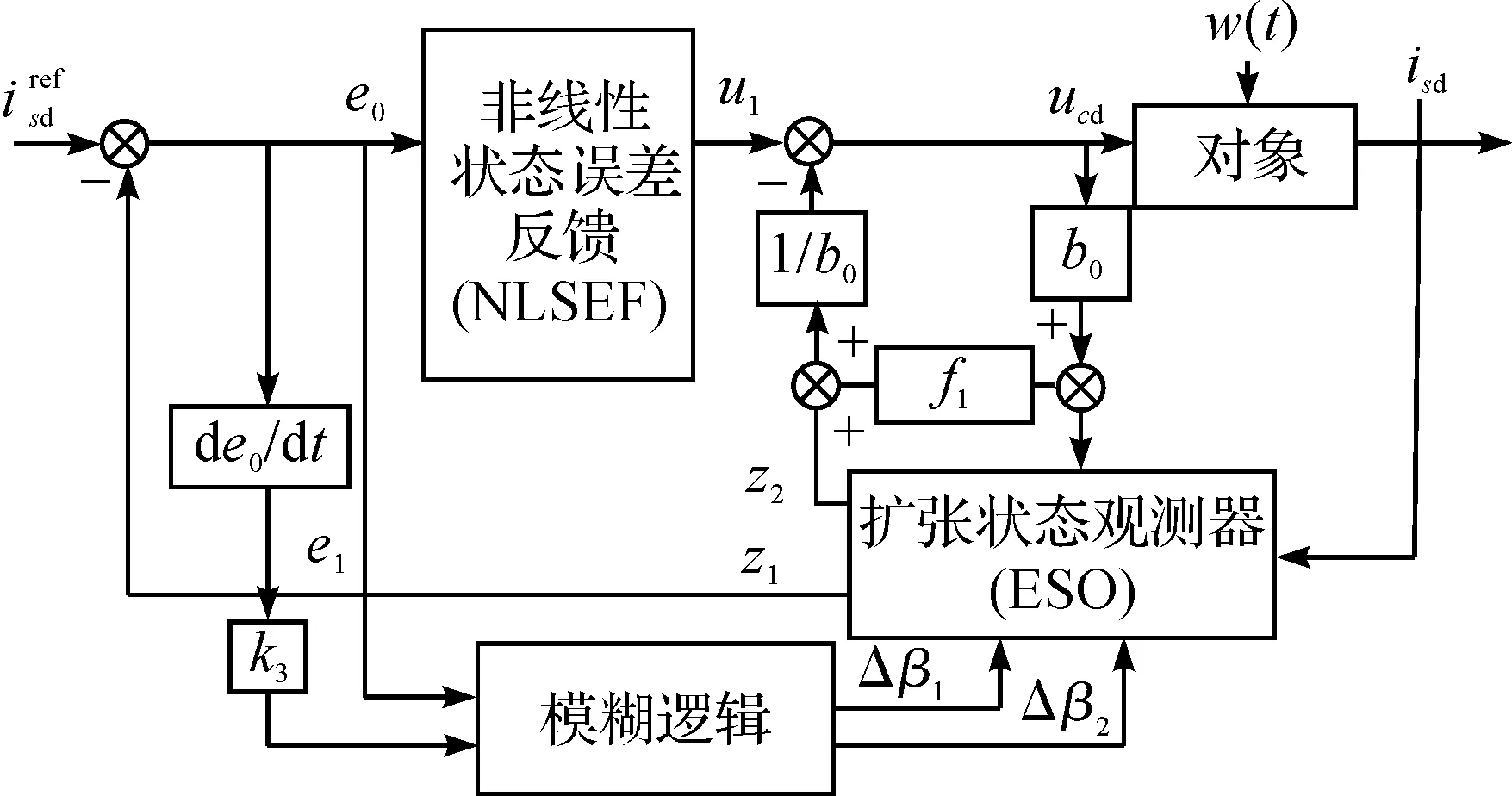
图4 模糊自抗扰控制器结构图Fig.4 Block diagram of FADRC controller

2.1 自抗扰控制器设计

将式(1)变换为自抗扰控制器的规范化形式，即

(4)

式中

(5)

由于在实际运行过程中，外部扰动不可避免，因此在考虑外部扰动以及参数不确定性的情况下，式(4)可改写为

(6)

式中：x1=[isd,isq]T，y=[y1,y2]T，f(x)=[f1,f2]T分别为系统已知扰动；w(t)为系统未知扰动；u=[ucd,ucq]T为控制器的输出量；b1=Δb+b0，b0为b1的估计值，一般根据经验获得，Δb为参数摄动值。定义x2=d=[d1,d2]T=w(t)+Δbu为系统扰动及不确定项。

由于式(6)可以看作两个一阶系统，因此在自抗扰控制器只需设计扩张状态观测器与非线性反馈控制律。以d轴为例，其表达形式有两种：

1) 扩张状态观测器

(7)

式中：y1为实测值；z1为y1的观测信号；e为观测误差信号；z2为d1的观测信号；β1，β2分别为正的观测器增益系数，选择适当参数值就能够实现较好的状态估计；g(e)为非线性函数形式，即

(8)

2) 非线性状态反馈控制器

(9)

式中：k为比例系数；δ为滤波因子，选择合适的参数可以避免高频震荡的发生；α为非线性常数，影响控制精度；Fal(e0,α,δ)函数为具有快速收敛的性能并且有一定的滤波效果，其表达形式为

(10)

d轴一阶非线性状态误差反馈控制律可取为

(11)

同理，q轴一阶非线性状态误差反馈控制律可设计为

(12)

式中：z4为d2的观测信号；u2为非线性状态反馈控制器输出信号。

2.2 模糊规则

模糊规则一般采用人的经验和知识的总结，考虑模糊规则时，有一些普遍的原则。笔者以跟踪误差e0以及e0的微分信号e1为性能指标，将e0和e1作为模糊控制器的输入，文献[11]中的模糊规则在线整定观测器增益参数β1和β2。其中，e0，e1分别为模糊变量；Δβ1，Δβ2分别为模糊规则输出量，并在其各自论域上分别定义5个语言子集为{负大(NB)，负小(NS)，零(ZO)，正小(PS)，正大(PB)}。选择输入量e0和e1的隶属度函数为高斯型(gaussmf)，输出量Δβ1和Δβ2的隶属度函数为三角形(trimf)[12]。由于e0实测值有一定抖动，故微分信号e1先经过增益环节然后输入到模糊控制器中。这里取e0，e1的基本论域分别为[-1,+1]和[-1,+1]，根据实际情况选定e0的比例因子为0.01，e1的比例因子为0.02，因此取Δβ1，Δβ2的基本论域分别为[-200,+200]和[-2 000,+2 000]。取k3为1/10 000。模糊推理采用Mamdani型，去模糊化算法采用加权平均法。模糊规则如表1所示。

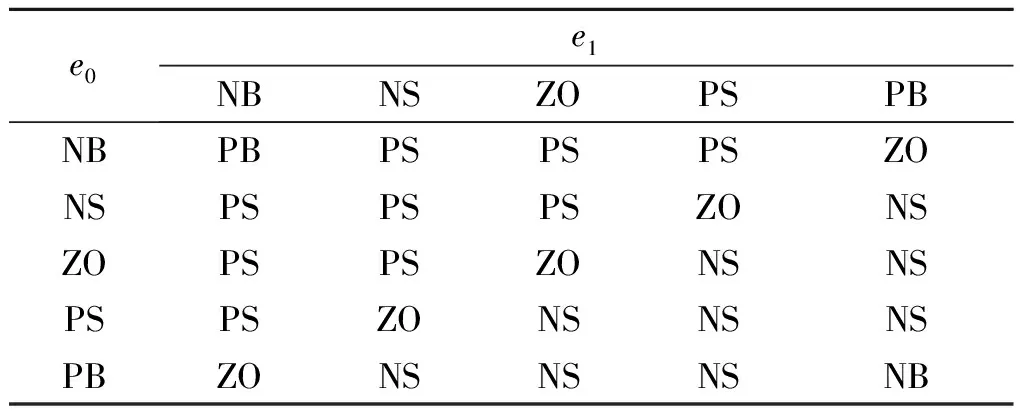
表1 模糊规则Table 1 Fuzzy rules

将表1中修正参数代入如下表达式，则有

(13)

当系统的数值计算采样步长h给定时，可采用步长法通过步长h确定β1，β2的初始值[13]，β1=1/h，β2=1/3h2。

3 外环控制器设计

根据不同的要求，VSC-HVDC系统可以实现有功功率控制、无功功率控制、电压下垂控制、定直流电压控制和定交流电压控制5种控制方式。VSC1以及VSC2必须一端采用定直流电压控制，而另一端须采用有功功率控制才能有效地保证直流端的稳定传输。VSC2采用定有功功率控制，VSC1采用定直流电压控制，而且VSC1和VSC2都能够实现对无功功率的独立控制[14]。

3.1 定直流电压控制器

不计换流站产生损耗时有，交流侧有功功率等于直流侧有功功率，即Ps=Pdc，当系统稳定运行时，式(3)中直流电压的微分为零，可得

(14)

当直流电压过低时，则增大相角差提高从交流侧流入直流侧的有功功率来对电容充电，提高直流电压；而当直流电压过高时则减小相角，减少流入的直流有功功率，使电容放电来降低直流电压。

3.2 功率控制器

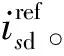
(15)

式中：Kp1，Ki1分别为定有功功率PI控制器参数；Kp2，Ki2分别为定无功功率PI控制器参数。

当交流侧与直流侧间的功率不平衡时，会造成直流电压不稳定,有功电流会向直流侧电容进行充放电,当直流电压再次稳定在给定值时停止。

4 仿真分析

通过Matlab/Simulink搭建了图1所示的两端VSC-HVDC系统，系统模型采用Silvano Casoria (Hydro-Quebec)模型。2个换流站均连接频率为50 Hz的交流系统，交流系统的容量为2 000 MVA，电压等级为230 kV；等效电阻R1=R2=0.1 Ω,C=70 μFL=7.5 mH；直流侧电压值udc=100 kV；系统的采样步长为7.406×10-6s，采用步长法确定β1，β2参数；内环ADRC参数β1=20 000，β2=100 000，b0=150，k=1，α=0.65，δ=0.2；外环PI参数Kp1=Kp2=3，Ki1=Ki2=3；有功功率1 p.u.= 200 MW，无功功率1 p.u.= 200 Mvar；直流线路使用75 km的直流电缆，具体参数如表2所示。

表2 直流输电线路参数值Table 2 Parameters of DC transmission line

针对3种不同内环控制器进行了仿真，内环ADRC控制器上文已给出，内环PI控制器参数P=0.6，I=6.0.

4.1 启动过程仿真

在启动阶段，控制系统在0.3 s时才开始启动，以防止过电流造成的影响。整流端的有功和无功功率的波形如图5所示，其中Ref为功率参考值；M1代表内环PI控制，外环PI控制；M2代表内环ADRC控制，外环PI控制；M3代表内环FADRC控制，外环PI控制。

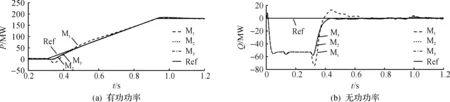
图5 VSC1有功和无功功率波形图Fig.5 Active and reactive power waveforms of VSC1

由仿真结果可知：PI控制在启动过程中有功功率、无功功率均有明显的超调，而ADRC和FADRC都能够快速的无超调的跟踪参考值。

4.2 交流系统三相短路故障仿真

在1.5 s时，逆变端交流系统发生三相短路故障，持续0.1 s。整流端有功和无功功率的波形如图6所示。

图6 VSC1有功和无功功率波形图Fig.6 Active and reactive power waveforms of VSC1

由仿真结果可知：当交流系统发生三相短路时，换流站立刻关断停止运行，有功功率迅速衰减到0，当故障消除后，系统慢慢恢复正常运行。以有功功率为例，仿真性能指标如表3所示。

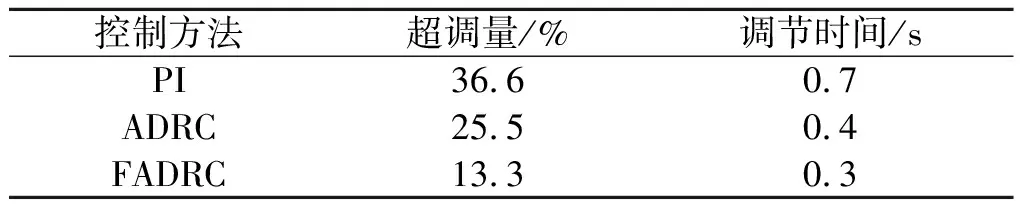
表3 有功功率仿真性能指标Table 3 Simulation performance index of active power

模糊自抗扰控制方法在抑制超调，暂态稳定方面有更好的效果。

4.3 逆变端系统交流电压扰动仿真

在4 s时，逆变端系统交流电压受扰减小至10%，持续时间0.1 s。整流端有功和无功功率的波形如图7所示。

由仿真结果可知：PI相对于ADRC以及FADRC受到干扰的影响更大，而FADRC在抑制超调，抗干扰能力方面优于PI以及ADRC控制。

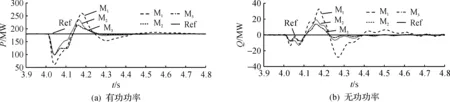
图7 VSC1有功和无功功率波形图Fig.7 Active and reactive power waveforms of VSC1

4.4 系统内部参数改变仿真

当增大逆变端电源的阻抗变为原来的3倍并保持其他参数及控制器参数不变时，在启动过程中比较整流端有功功率基于PI控制与FADRC控制的效果。整流端有功功率的波形如图8所示。

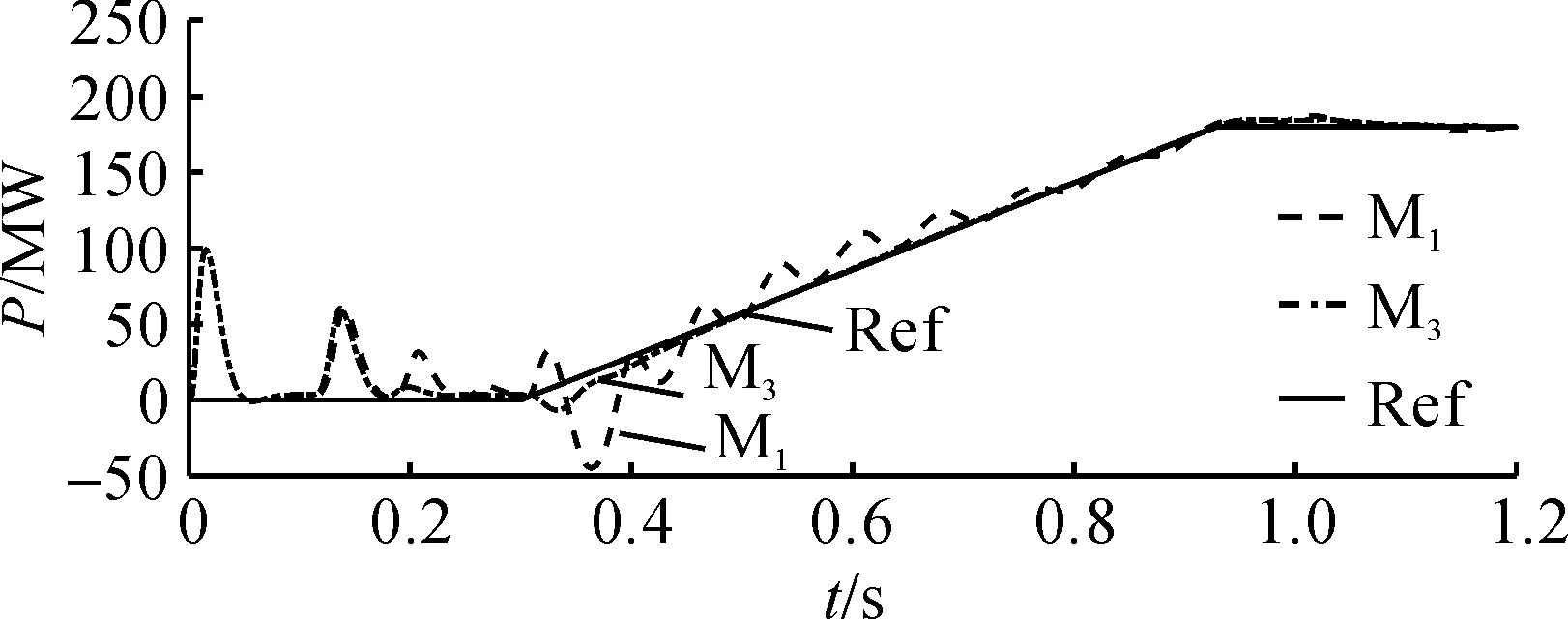
图8 VSC1有功功率波形图Fig.8 Waveform of active power

由图8可以看出：PI 控制有很大的波动幅度，而FADRC控制几乎不会引起变化。证明了FADRC有更强的鲁棒性，有效地抑制了系统参数改变带来的影响。

通过上面4种仿真对比分析可以得出：自抗扰控制器能够估计系统不确定性及扰动，并且能够对系统进行补偿，使得系统的鲁棒性和抗干扰性能力得到提高这是PI控制所不具备的，通过模糊规则在线整定参数能够进一步提高自抗扰控制器的鲁棒性。

5 结 论

针对电压源型换流器高压直流输电系统的非线性、多变量和强耦合的特点，且系统中存在的不确定性参数及扰动等问题，首先建立高压直流输电系统的数学暂态模型并设计双闭环控制器结构，内环控制中设计模糊自抗扰控制器。通过对自抗扰控制器的参数调节方法进行研究，并选取合适的参数，能够实现电流解耦功能且能够估计系统不确定性及扰动并进行补偿，同时设计模糊规则在线整定扩张状态观测器参数，进一步提高自抗扰控制器的鲁棒性。通过仿真和实验表明，所设计的模糊自抗扰控制器能够有效提高系统的鲁棒性以及抗干扰性。