一种基于多视觉传感器的刚体位姿估计方法
,, ,
(浙江工业大学 信息工程学院,浙江 杭州 310023)
基于视觉传感器的移动目标位姿估计在视觉伺服[1]、移动目标跟踪[2]和视觉定位[3]等领域有着广泛的应用。目前, 大多数研究都是基于相机(视觉传感器)内参已知的前提下, 通过相机获取图像并加以处理, 得到图像中的2D特征信息, 利用2D-3D坐标系间的对应关系来设计位姿估计方法以实现对目标位姿的估计。基于单个视觉传感器的目标位姿估计方法按所提取图像特征的不同主要分为以下几类:1) 基于点特征的位姿估计方法; 2) 基于线特征的位姿估计方法; 3) 基于轮廓的位姿估计方法。其中, 第一类方法是利用移动目标上的一系列已知的特征标记, 通过基于点特征的位姿估计方法求解目标的位姿[4-6]。第二类方法通常都是由第一类方法演变而来, 尤其是针对某些线特征易于提取的目标, 通过建立所提取的线特征与3D 空间中目标线段之间的对应关系, 采用相应的位姿估计算法估计目标位姿[7-8]。第三类是基于目标的3D模型已知的情况下, 利用2D图像提取的目标轮廓构建与3D 模型轮廓的对应关系, 并采取某些优化方法不断减小估计误差[9]。在上述的三类方法中, 第一类方法适用性最广, 究其原因有二: 其一, 相对于第二和第三类方法, 第1)类方法可更直接更方便地建立2D-3D 对应关系; 其二, 便于人为地创造一些mark点以加速点特征的提取。在现有的研究中, 大多数研究都是基于点特征的, 并存在一些相对成熟的点特征位姿估计方法, 例如OI正交迭代法[10]、Epnp算法[11]及自适应扩展卡尔曼方法(AEKF)[13]与迭代自适应扩展卡尔曼方法(IAEKF)[12]。在上述的四种方法中, 前两者的估计精度过分依赖观测噪声, 当噪声过大时, 它们的估计精度便会急剧下降, 在这种情况下, AEKF 方法[13]被提出, 它通过估计每一个采样步长中的过程噪声和观测噪声来克服环境中噪声过大或者环境发生异变时产生的影响, 增加了系统的稳定性, 相对于AEKF, IAEKF将AEKF 的结果进行迭代, 使其估计方差最小以达到提高精度的目的, 但付出的计算量却远超AEKF。在某些极端状况下, 如相机标定误差过大、初始值误差过大, 基于单个视觉传感器的估计方法所得到的估计结果误差过大甚至发散。基于多个视觉传感器的集中式融合估计方法[14], 结合多个视觉传感器提供的图像信息, 采用AEKF或者IAEKF估计目标的位姿, 在一定程度上弥补了单视觉传感器方法的不足, 提高了系统的估计精度, 但随着观测信息的增加, 观测矩阵维数上升, 集中式融合方法消耗的计算资源成平方增长,导致系统的响应速度大大降低。
为此, 笔者提出了一种应用于多视觉位姿跟踪系统的分布式融合方法, 以此来提高系统的运行效率。分布式融合方法[15]是对各个局部估计结果按照一定的方法进行加权得到全局最优值, 避免了观测矩阵扩维, 而且可采用多线程编程方式同时计算多个局部估计结果, 大大降低了运算时间。主要内容描述如下:首先, 根据实验环境建立观测模型与刚体运动学模型; 其次, 以AEKF为局部滤波器, 提出了应用于多视觉传感器位姿估计系统的分布式融合方法; 最后, 通过对比实验, 以精度和系统的响应时间为指标, 验证基于AEKF的分布式融合方法应用于目标位姿估计问题的有效性和优越性。
1 平台简介
如图1所示, 本实验平台包括一台PI公司生产的6 足位移台和两个固焦相机(型号为今贵 S9)。

图1 实验平台Fig.1 Experimental platform
两个相机分别固定在平台一旁, 被跟踪目标固定在6 足位移台上部, 随6 足位移台而运动, 6 足位移台实时反馈状态信息(位置和姿态), 如图2所示, 在6 足位移台初始化状态下, 6 足位移台坐标系Ow′-Xw′Yw′Zw′与世界坐标系Ow-XwYwZw重合, 6 足平台实时反馈的位姿信息即是6 足位移台坐标系原点在世界坐标系的位姿信息, 6 足位移台反馈位姿精度可达微米级,所以可将该反馈位姿信息作为真实位姿。

图2 世界坐标系与位移台坐标系Fig.2 World coordinate system & 6 axis hexapodcoordinate system
2 系统模型
为了将所提出方法的估计结果与真实结果进行对比, 设定系统的状态变量为基于世界坐标系下的6 足位移台坐标系原点的位置、姿态及对应的速度、加速度, 系统的观测是二维像素坐标系中特征点的像素坐标, 它与状态变量存在着一定的约束关系。因此, 在下面的描述中, 首先介绍了像素坐标系与世界坐标系之间的转换关系,并以此建立系统的观测模型; 其次, 利用加速度模型描述了移动目标的运动情况。
2.1 观测模型的建立
如图3所示, 本系统涉及的坐标系包括:像素坐标系Opix-upixvpix, 图像坐标系Op-xpyp, 相机坐标系Oc-XcYcZc, 物体坐标系Oob-XobYobZob,6 足位移台坐标系Ow′-Xw′Yw′Zw′及世界坐标系Ow-XwYwZw。

图3 6 个坐标系之间的关系示意图Fig.3 The relationship between the six coordinate systems

像素坐标系与图像坐标系之间的关系为
(1)

图像坐标系与相机坐标系之间的关系为
(2)
式中f为相机的焦距。
相机坐标系与物体坐标系之间的关系为
(3)
式中supTsub为sup坐标系与sub坐标系之间的转换矩阵, 由3×3的旋转矩阵supRsub与3×1的平移矩阵supTsub组成, 且supTsub= (subTsup)-1。结合上述坐标系之间的转换关系, 可以得到像素坐标系与物体坐标系之间的转换为
(4)
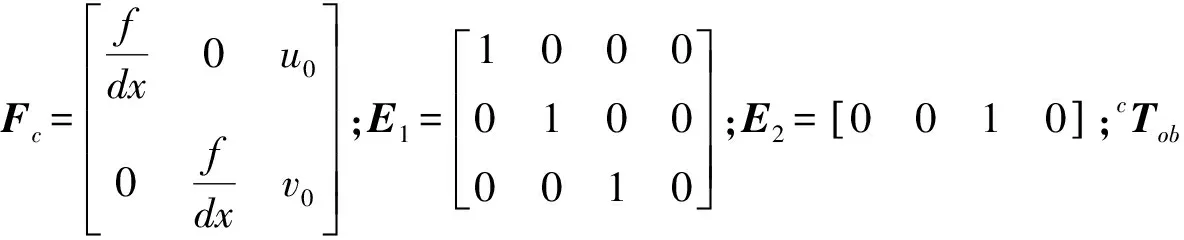
综上, 系统的观测方程可表示为
z(k)=h(x(k))+r(k)
(5)


2.2 跟踪目标的加速度运动模型
记k时刻运动目标状态为x(k), 其具体形式为

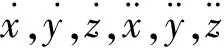
x(k)=Fx(k-1)+q(k-1)
(6)
式中:δt为采样时间;I3×3为3×3的单位矩阵;q(k-1)为过程噪声,服从均值为零、协方差为Q(k-1)的高斯分布。
3 基于多视觉传感器的分布式融合方法
3.1 AEKF局部估计器
EKF方法通过对非线性函数的泰勒展开式进行一阶线性化截断, 来处理非线性问题。为了进一步提高估计精度, 提出了基于自适应方法的扩展卡尔曼滤波器,自适应方法包括基于相关性方法(Correlation based algorithms)、极大似然方法(Maximum likelihood algorithms)和方差匹配方法(Covariance matching algorithms)[12]等等, 其中方差匹配方法较其他两种方法具有更高的计算效率。基于方差匹配的扩展卡尔曼滤波方法可描述如下:
首先, 根据系统模型计算状态的预测值和观测的预测值分别为

(7)
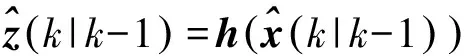
(8)

P(k|k-1)=FP(k-1|k-1)FT+Q(k-1)
(9)
式中P(k-1|k-1)为k- 1时刻的状态误差协方差矩阵。由于系统的观测方程是非线性的, 对观测方程求关于状态预测值的一阶偏导作为观测矩阵,即
(10)
为了计算观测噪声的协方差, 根据观测残差向量
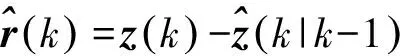
(11)
并通过前N个时刻可计算当前时刻的观测噪声协方差方差矩阵为
(12)

再根据上述计算得到的状态预测误差协方差矩阵、观测矩阵及观测噪声方差矩阵计算当前时刻的卡尔曼增益, 进而计算状态的估计值并更新状态误差协方差矩阵为
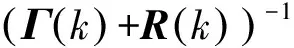
(13)

(14)
P(k|k)=P(k|k-1)-K(k)H(k)P(k|k-1)
(15)
最后,更新过程噪声协方差矩阵, 计算方法与求取观测误差方差矩阵类似,即

(16)
(17)

3.2 分布式融合算法
在卡尔曼滤波器中, 计算滤波增益时, 涉及新息矩阵的求逆, 若采用观测扩维的方式, 将很大程度上增加系统的计算量。而分布式融合算法是对各个局部估计结果按照一定的方法进行加权得到全局最优值, 避免了观测扩维, 从而达到减小计算负担的目的。下列所述的分布式融合算法已被证明等价于集中式算法[16],描述如下:
融合中心根据先验信息计算k时刻状态预测值及其对应的误差协方差分别为
(18)
P(d)(k|k-1)=FP(d)(k-1|k-1)FT+Q(d)
(19)
式中:x(d)(k-1|k-1),P(d)(k-1|k-1)分别为k-1时刻分布式融合状态的估计值和误差协方差矩阵, 然后结合各个局部滤波器的状态和误差协方差的预测值与估计值, 更新融合中心的误差协方差矩阵及融合后的状态估计值分别为

(20)

(21)

3.3 基于多视觉传感器的分布式融合方法
结合3.1,3.2所述,基于多视觉传感器的分布式融合方法可描述如下:



4 实验及分析


物体坐标系与6 足位移台坐标系之间的转换矩阵为
在被跟踪目标上标记8 个特征点以便实时提取, 8 个特征点在物体坐标系下的坐标分别为(-35,-80,0),(35,-80,0),(35,-10,0),(-35,-10,0),(-20,-65,0),(20,-65,0),(20,-25,0),(-20,-25,0),单位为mm。需要说明的是, 在理论上, 每个采样时刻的局部过程噪声方差与融合中的过程噪声方差是统一的, 但是由于存在数值计算误差, AEKF局部估计的两个过程噪声方差可能会不同, 在此, 令融合过程噪声协方差Q(d)为局部过程噪声协方差的均值。
实验时, 为了便于分析实验结果及算法的运行时间, 采用以下步骤进行实验: 首先, 利用设计的上位机系统及实验平台, 以20 Hz的采样频率实时提取特征点的像素坐标及记录当前时刻6 足位移台所反馈的姿态信息, 并保存; 其次, 将保存的数据代入已编写好的Matlab程序中, 得到估计结果及算法运行时间。
图 4,5 给出了基于AEKF的集中式融合方法和基于AEKF的分布式融合方法对目标位置和姿态的估计结果曲线, 直观地看, 分布式融合方法与集中式融合方法的估计结果曲线几乎重合, 说明分布式融合方法的精度接近甚至等于集中式融合方法的精度。
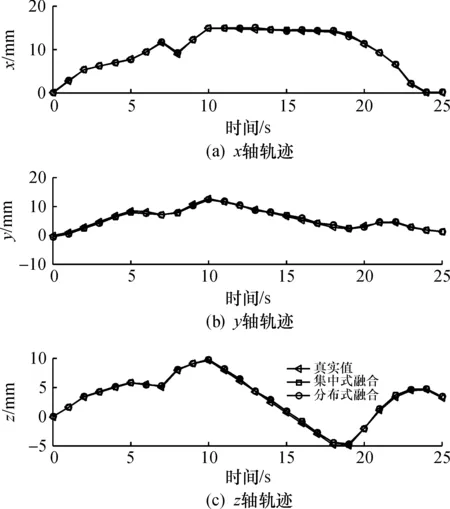
图4 AEKF位置估计结果Fig.4 Position estimation results based AEKF

图5 AEKF姿态估计结果Fig.5 Posture estimation results based AEKF
为了更加清晰、直观的分析各个滤波器的估计精度, 表1给出了基于AEKF的局部估计误差和融合估计误差的统计信息, 包括最大误差、误差均值及误差的方差。从表1中可看出:融合估计误差均值及方差都要小于对应的局部估计结果, 表明通过信息融合提高了估计精度, 分布式融合方法与集中式融合方法的估计误差均值及方差相近, 再次证明基于AEKF的分布式融合方法能保证系统的估计精度。
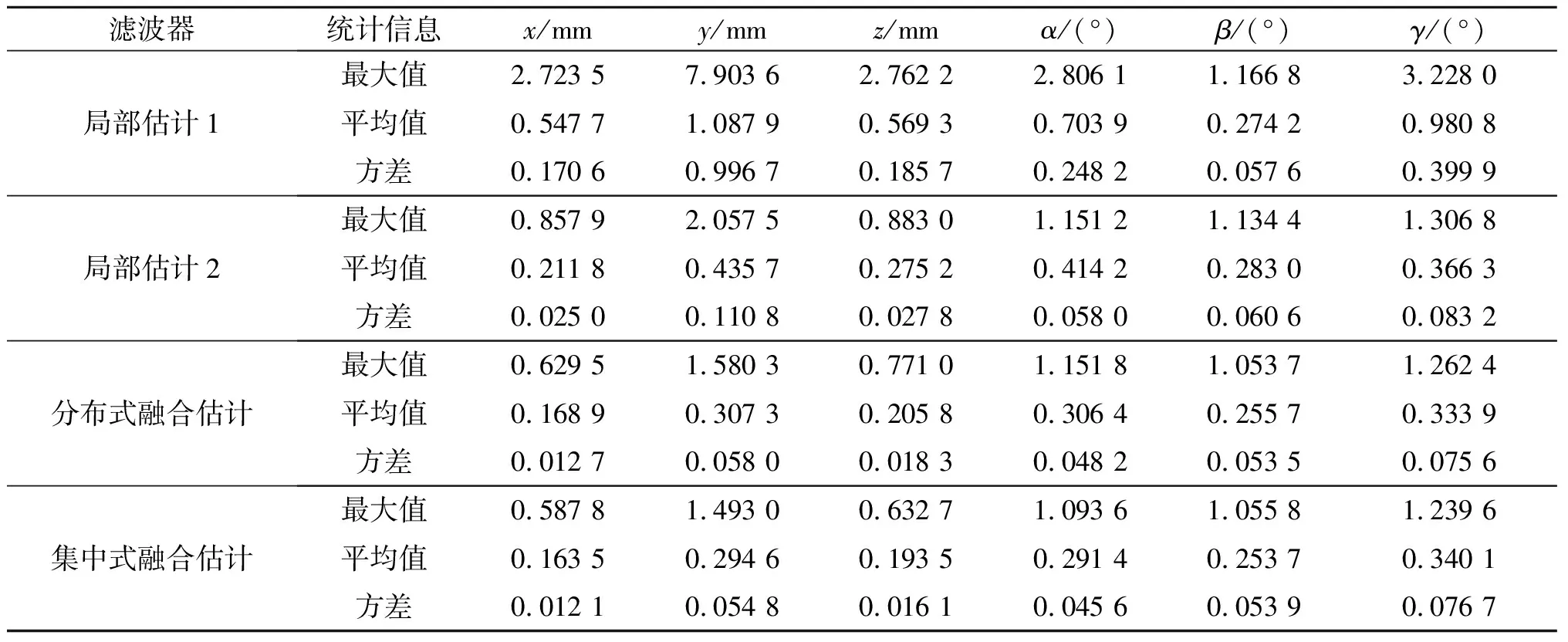
表1 基于AEKF的各个滤波器误差统计Table 1 Error statistics of each filter based AEKF
表2给出了各个滤波器每次估计状态信息的运行总时间, 这个实验结果是基于Core i5-2450 2。5 GHz双核CPU及6 GB RAM的硬件平台所得到的, 从表2中可以看出: 基于AEKF 的分布式融合方法的运行时间要明显小于集中式融合方法的运行时间。结合上述实验结果表明:基于多传感器的分布式融合估计方法在保证精度的前提下, 能大大提高系统的运行效率, 证明了所提出方法的有效性和优越性。

表2 各个滤波器运行时间Table 2 Running time of each filters
5 结 论
在基于多视觉传感器的移动刚体估计系统中, 针对于集中式融合方法消耗过多的计算资源的弊端, 提出了一种基于多视觉传感器的分布式融合方法。笔者将自适应扩展卡尔曼滤波器作为局部估计器, 得到各个视觉传感器的局部估计结果, 再运用分布式融合方法得到融合估计结果。通过实际实验验证:与自适应扩展卡尔曼集中式融合方法进行相比, 所提出的方法在保证估计精度的同时, 能有效提升系统的运行效率, 降低了系统对高性能硬件的依赖程度。

