用ArdUino智能设计重现经典物理实验

陈染

智能设计不仅在工程设计、人文艺术领域有着广泛的应用，改善我们的生产生活和艺术体验，它更是科学探索的重要工具，能够准确高效地收集实验数据，进行数据分析，帮助我们更好地认识实验现象。在前沿科学研究中，我们几乎找不出一个不使用智能设计的科研项目。

智能设计也从科学研究延伸到基础教育领域，帮助开展和辅助科学实验，认识科学原理。以Arduino为代表的开源硬件成为了科学探索主题智能设计的热门载体，与物理、化学、生物等学科结合起来，用科学的思维方式探索研究问题。

而基础教育也有开展数字实验的实际需求。《普通高中物理课程标准》的实施建议中提出“要重视数字实验，创新实验方式。学校要重视引导教师研究数字实验系统对传统实验的改进方法，研究数字实验系统的教学方式，促进教学手段与方式的现代化”，课程的需求成为了科学探索主题的智能设计与课程相结合的依据。

目前，实施物理数字实验探索的主要工具是数字化信息系统（Digital InformationSystem，简称DIS）。数字化信息系统的基础器材是各式各样的传感器，与传统实验方法相比，实验器材简化了很多，灵活度也高很多：同一个传感器可以完成不同的实验，同一个实验也可以用不同的传感器完成；数字化信息系统用计算机收集和处理数据，数据的精确度比传统实验更高。

但数字化信息系统与传统实验相比，仍有一些不可回避的问题。在硬件方面，数字化信息系统普及率较低，价格较高，适配的物理实验较少；在教学方面，一部分学生在数字化信息系统上只是学会了器材的连接方法和机械地收集数据，对实验原理仍不甚了解，无法真正理解实验的意义。

将智能设计课程与学科结合起来，用Arduino进行数字化信息系统的设计，这种方法能够在一定程度上发挥数字化信息系统的优势，规避数字化信息系统的问题。接下来我们通过“单摆的等时性”和“测量地球质量”两个经典物理学实验案例，认识如何通过智能设计完成科学探索的过程。

用Arduino验证单摆的等时性

摆是一种实验仪器，最基本的摆称为单摆，它由一条绳或杆和一个锤组成，锤系在绳的下方，绳的另一端固定。我们可以通过单摆研究一些力学现象，例如，单摆的一个重要特征就是在小角度（摆角小于5°）的条件下具有等时性。

伽利略在1583年首先用科学的方法研究了摆的等时性。有一天，他看到比萨大教堂的吊灯在轻轻晃动，每次吊灯晃动的时间好像是一样的。于是，伽利略用脉搏粗略计算了吊灯的摆动周期，发现确实跟猜想的一样。那么，单摆的周期跟什么因素有关系呢？通过实验，伽利略发现了单摆的周期与摆的质量没有关系，只与摆线长度有关。伽利略将这个结论记录在他的科学名著《关于两种新科学的对话》上。后来，惠更斯在伽利略的基础上对单摆进行进一步研究，出版了著名的《摆钟论》，并发明了摆钟。一直到20世纪30年代，摆钟都是人们最准确的计时工具。

伽利略用脉搏计算了大吊灯摆动的周期，这是一个很粗略的方法，如果16世纪有智能设计，伽利略会怎么做呢？接下来这个实验，我们穿越到16世纪，化身伽利略，用智能设计探究单摆的周期与什么因素有关。

现在我们在课本中学到，单摆的周期公式是其中，T是单摆的周期，L是摆绳长度，g是所受的重力加速度，约等于9.8m/s2。但伽利略那个时代可不知道这些，我们需要设计一个实验，探究“单摆周期与摆绳长度的关系”。

在实验开始之前，我们需要明确自变量是什么、因变量是什么，才能知道如何探索它们之间的关系。在这个研究中，自变量是摆绳长度，因变量是单摆周期。此外，我们需要控制一些不必要的因素，如摆的质量、摆角等。

最开始时，伽利略用脉搏的跳动判断了吊灯的摆动周期，但这个方法只是粗略的时间估算，很容易产生人为误差。因为在不同情绪下人的脉搏跳动的节奏不同，计时的开始和结束都会产生误差等。而Arduino智能设计就能很好地避免这些问题：非接触式传感器能够很好地启动和结束计时，而且不影响单摆运作，Arduino毫秒级的计时远远比人的时间感知更为准确。所以，我们用非接触式传感器测量单摆的周期更加合适。

非接触式传感器类型有很多，哪一种传感器最适合单摆周期的测量呢？不同的学生有不同的答案，我们可以鼓励学生讨论并尝试用不同的传感器制作模型，探究不同的传感器的优势和劣势分别在哪里。

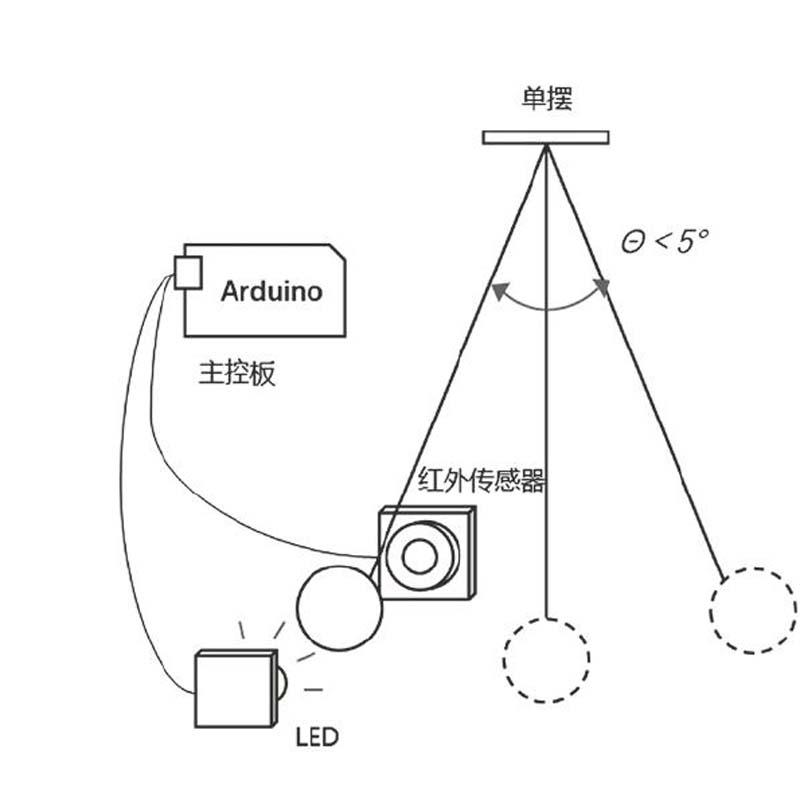
例如，我們可以选择用LED灯和红外传感器制成红外阻隔装置，作为实验的测量器。未受到阻隔时，LED灯的光线被红外传感器感测到；当摆锤经过传感器和LED灯之间时，光线受到阻隔，这时候就可以启动或停止计时器，开始一次实验的计时。

将Arduino元件和实验装置安装完毕，测量在不同摆线长度下摆动周期变化的规律，每一次实验都要重复进行，以减小误差。经过多次测量，我们获取了不同摆长下的周期数据，就可以进行接下来的数据处理，寻找自变量与因变量的关系。我们也可以将Arduino与电脑相连接，进行数据的直接处理。

这个案例的思路比较直接，测量数据比较简单，但并不是每一种实验都能这么直接地找到测量的方法，接下来的案例“用Arduino测量地球质量”就没有那么直接了。

用Arduino测量地球质量

人们对于地球的探索从古至今都未曾停止过，不断地推进新科学的发展。古希腊的埃拉托斯特尼用巧妙的方法测量了地球的半径，但人们对地球有多重这个问题却在很长时间内没有取得任何进展。

直到17世纪，牛顿的万有引力研究为人们测量地球质量带来希望。万有引力定律指出，两个质点彼此之间相互吸引的作用力，与它们的质量乘积成正比，并与它们之间距离的平方成反比。这就是我们熟悉的万有引力公式

有了万有引力定律，理论上我们测量一个物体与地球之间的吸引力，再测量它与地球质心之间的距离，就可以知道地球的质量是多少了。但希望的火花很快就熄灭了，地球上物体之间的万有引力太微弱了，牛顿无法计算出关键的引力常数G的大小，他甚至认为我们无法在地球上计算地球的质量大小。

但人们对于地球质量的探索并未就此停歇，18世纪末，卡文迪许设计了极为精妙的扭秤实验，通过扭秤将极为微小的引力进行2次放大，计算出万有引力公式中最为关键的引力常数G，并根据这个实验测得地球质量。

想象一下，我们化身为带着Arduino的卡文迪许，怎么样用智能设计计算地球质量呢？

这个方法可能不像测量单摆等时性的方法那样直接。我们知道了地球的半径，知道了引力常数G，意味着我们只需要知道万有引力F和另一个实验物体质量m就能用智能设计计算出地球的质量。Arduino。可以搭配丰富的传感器，但这些传感器在测力方面却不是很擅长，所以，我们需要将万有引力转化成方便用传感器检测的东西。

我们可以根据牛顿第二定律将力的测量转换成对加速度的测量。牛顿第二定律描述的是物体加速度的大小跟它受到的作用力成正比，跟物体的质量成反比。重力公式F=mg是牛顿第二定律的一个特别形式，其中，F为重力大小（通常写作G，但为了防止与引力常数混淆，这里写作F），g是重力加速度。将它和万有引力公式联立起来，就可以将传感器难以测量的力转化为测量加速度：

公式的转换让我们将一个难以用智能设计测量的力转变成了容易测算的加速度，这时候我们可以用加速度传感器进行数据收集和计算了。但如果没有加速度传感器怎么办呢，用同样的思路，我们还可以根据自由落体公式将重力加速度的测量转变成对时间的测量。当静止物体做自由落体运动时，公式如下：

其中，S为下落距离，t为下落时间，g为重力加速度。转换一下，即成为：

这样，我们又完成了一次测量要素的转换，将加速度的测量转换成时间的测量。接下来就是选择合适的传感器，完成时间的测量。同样，我们可以尝试用不同方法解决问题。这里我们提供一个设计方案：重球从一定高度垂直下落，在开始下落的地方红外传感器制成红外阻隔装置，用于判断重球是否落下，在重球落点的正下方安装压电传感器，判断重球是否落下。重球未落下时，红外传感器处于被阻隔的低电平状态；一旦下落，红外传感器感测到光线，开始计时。当重球落到压电传感器上时，传感器由低电平转变为高电平，计时结束。通过2个时间相减，我们就能得知重球下落的时间。多次收集数据后，进行数据分析，并通过公式计算出地球的质量。

在这个设计中，我们用到了2种类型的传感器：非接触式红外传感器和接触式压电传感器，无论选用哪种传感器，我们的目的都是为了让实验数据更加准确。我们还可以尝试其他传感器，用不同的方案测量数据，试一试哪一种方案是最佳选择。

上面介绍的“验证单摆的等时性”和“测量地球的质量”是2个典型的用智能设计进行科学探索的案例。它们的设計背景都建立在大科学家的著名实验上，踵武前贤，我们能够体会到大科学家是通过怎样的思路研究这些重要的科学问题的。我们还用到了智能设计，让它成为收集更高精度数据的帮手。

在器材方面，用Arduino智能设计重现经典实验的方案选择更加多样化、更加灵活。就像用Arduino测量地球的案例一样，没有测力计，我们可以将力的测量转换为加速度的测量；没有加速度计，我们还可以转换成对时间的测量；在对时间的测量上，我们还可以选择用不同的传感器完成。

在教学方面，用Arduino智能设计重现经典实验更能让学生对科学知识有更深入的理解。与数字化信息系统相比，Arduino智能设计的过程更加复杂，学生需要对问题有一个初步的认识，规划设计路线，自己动手制造实验设备，编写Arduino代码，进行调试和实验，处理实验数据。复杂的实验过程让学生建构起对科学的理解，而灵活的设备让学生对设计方案有了更多自主的选择，在多种方案比较中学生能够更深入地掌握科学知识。