一种基于截断机制的稳态优化算法求解多目标优化问题

荆东星 张清安

(湘西民族职业技术学院计算机系 湖南 湘西 416000)

0 引 言

许多实际优化问题，通常需要同时求解2～3个高度复杂、非线性并且带有冲突性的目标[1]。这类问题通常被定义为多目标优化问题(MOPs)。而多目标优化算法(MOEAs)非常适合于求解此类问题。因此，在过去的几十年里，MOEAs得到了飞速发展，并在工程领域得到广泛应用[2-4]。

对于MOPs来说，MOEAs的一个关键优势是基于种群特性，它允许种群中的个体在单个执行过程中同时收敛到Pareto面的不同区域。一般来说，可以将MOEAs的优化目标简单归纳为以下两个方面[5]：

1) 收敛：将种群到MOP的Pareto面的距离最小化。

2) 分布：种群广泛且均匀的分散在MOP的Pareto面上。

为了实现以上目标，近年来，研究者提出了大量有效的MOEAs[6]。而根据其每次进化过程中产生的子代个数可以将现有的MOEAs大致分为两类：一类是基于种群进化的MOEA[7]；另一类是基于个体进化的稳态MOEA[8]。第一类中，具有代表性的算法有Zitzler等提出的SPEA[9]及其改进版本SPEA2[10]，Srinivas等[11]提出的NSGA，以及Deb等[7]在此基础上提出的NSGA-II等。而第二类的代表性算法则有Deb等[8]提出的ε-MOEA。基于种群的MOEA一直备受关注，而基于个体的稳态MOEA自从2006年被提出后，在多目标优化领域鲜有文献出现。

因此，本文首先分析ε-MOEA所存在的问题，然后提出一种基于截断机制的稳态MOEA。该算法首先采用Pareto支配控制进化种群和归档种群的收敛性，然后采用一种新的截断机制维持归档集种群的分布性能。另外，本文的算法除默认参数外(如：种群大小，变异率，交叉率等)，无需任何参数。通过实验比较分析可以发现，本文算法在求解2～3维MOPs时，能够获得良好性能(收敛性和分布性)的解集。

1 基本概念

1.1 问题描述及相关性质

为了便于描述，本文所采用的优化问题为最小化问题。一般地，最大化问题通常也可以通过公式转换为最小化问题，问题的表达形式可以定义如下：

minimizeF(x)=f1(x),…,fm(x))T

(1)

s.t.gi(x)≥0j=1,2,…,J

hk(x)=0k=1,2,…,K

x∈Ω

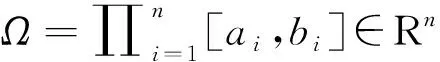
在多目标优化中，以下概念得到了很好的定义和广泛应用。

1) Pareto支配：对于两个不同的解，x1，x2∈X,如果满足式(2),则认为x1支配x2，并可以用x1x2表示。

(2)

2) Pareto最优解集：对于单个解x*∈X，如果不存在其他解x′∈X满足x′x*，那么它将被视为Pareto最优解。所有Pareto最优解构成了Pareto最优解集。

1.2 稳态MOEA模型

2003年由Deb等人首次提出稳态MOEA[8]，为多目标优化研究提供了一条新的思路。稳态MOEA中，两个种群(进化种群EA和归档集Archive)同时进行优化。首先通过随机初始化生成初始EA种群，将该种群的非支配解集存入到Archive内，然后分别从EA和Archive中随机挑选一个个体(如图1中的p和e)进行交叉变异操作生成一个新的子代个体c。最后根据EA保留机制和Archive保留机制分别判断子代个体能否被EA种群或Archive种群接纳。其示意图如图1所示。

图1 稳态算法模型

一般而言，EA保留机制采用的是Pareto支配策略，通过Pareto支配策略将收敛性好的个体保留下来。而Archive保留机制不仅需要考虑种群的收敛性，还要保证种群能够均匀且广泛地分布在整个Pareto面上。例如，ε-MOEA的Archive保留机制采用的是ε-支配策略来保证种群的收敛性和分布性。

2 ε-支配的缺陷

ε-支配方法是由Laumanns等[12]提出，主要思想是根据值将目标空间划分为若干个网格，每个网格内只允许一个个体存在。因此，当两个解p、q满足下式条件时，认为pε-支配。

(1-εi)·fi(p)≤fi(q) ∀i∈{1,2,…,m}

(3)

式中：p和q为目标空间的两个解；m为目标的维度。

图2给出了ε-支配的示意图，个体p的ε-支配范围为ABCDA所围绕的区域，而原始Pareto支配范围为PECFP构成的区域。可以发现，ε-支配的区域要明显大于Pareto支配的区域。在ABCDA区域的个体都将被p支配掉。另外，当同一个网格内存在多个解时，如图2中的1和2，ε-支配需要从中选择一个性能最好的解保留下来。首先判断这些解的Pareto支配关系，只考虑其中的非Pareto支配解。然后从中挑选距离所在网格的圆点最近的个体。在图2中，解1离网格圆点更近，因此它将被保留。

图2 ε-支配

进一步发现，种群的大小以及性能都依赖于值的设置，当ε值设置过大，种群的数量将会过小，MOPs的某些区域可能很难搜索到；而当值设置过小，种群的数量则会过于庞大而限制算法的优化速度。如何为特定问题设置合适的值没有一个很好的解决方案。另外，ε-支配很难保证种群的广泛性，因其特有的性质，位于Pareto面边界的解很容易被支配掉[13]。如图3所示，目标空间被划分为400个均匀网格，网格的宽度等于ε。根据ε的性质，在目标空间中最大能够容纳20个非ε支配解，然而ε-支配策略实际只能允许12个非ε支配解在目标空间中。因为这些解将会把与所在网格平行或垂直的其他网格中的所有解支配掉。从图3中解的分布可以发现，靠近边界的解的分布要比中间位置的稀疏。

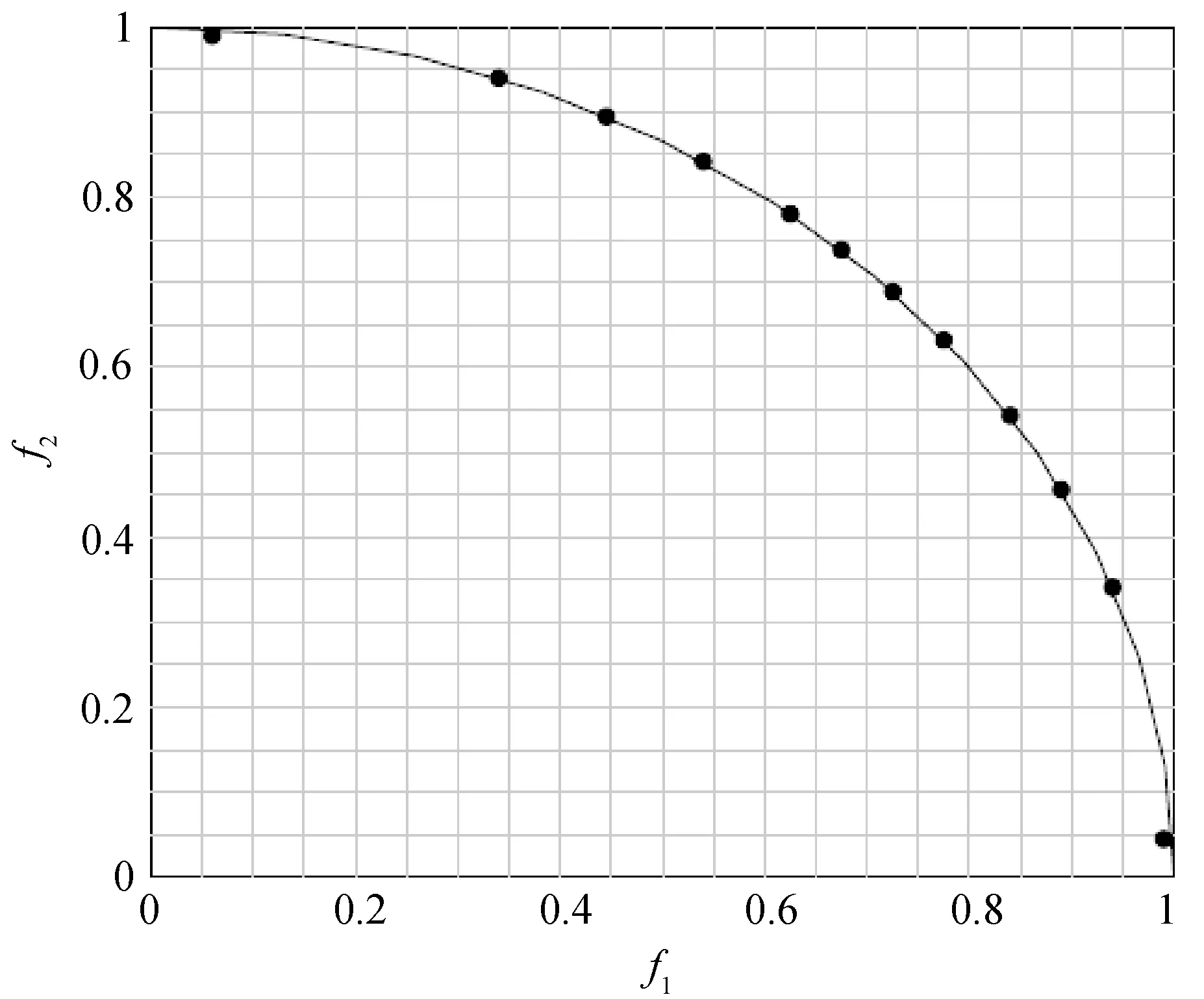
图3 非支配解集

为了使得Archive中的解的数量可控，且具有良好的性能。本文对ε-MOEA的Archive保留机制进行了修改，并提出了一种新的稳态优化算法。

3 一种新的稳态算法

在本文提出的算法(PTEA)中，采用了Pareto支配以及截断机制来共同维持Archive种群的性能。Pareto支配维持Archive种群的收敛性，截断机制维持Archive种群的分布性。

在截断机制中，首先采用欧氏距离计算各个个体之间的距离，然后选择最短距离的两个个体，再判断它们第二短的距离。如果第二短的距离也相等再判断它们第三短的距离，依次类推，直到找到距离不一样为止，然后删除距离短的个体。其与SPEA2的修剪类似，唯一区别是SPEA2只考虑了两次比较。而当维度达到3维时，在目标空间中可能存在多个第二短距离相等的情况。

PTEA的算法步骤如下：

Step1初始化参数。设置种群大小N，最大进化代数MAXGEN，交叉率Pc，变异率Pm。

Step2初始化种群。采用随机初始化方法初始化大小为N的EA种群。

Step3构建初始Archive。将EA种群进行Pareto非支配排序，将非支配解集复制到Archive中。

Step4生成单个子个体。从EA种群和Archive种群中随机挑选一个个体进行交叉变异产生新个体。

Step5更新EA种群。如果子代个体被EA种群中的个体支配，不考虑更新。如果EA种群中不存在个体支配新的子代，判断EA种群是否存在个体被子代支配。如果存在则随机替换一个被支配的个体，如果不存在，则随机替换EA种群中的个体。

Step6更新Archive种群。首先判断子代与Archive种群中个体的支配关系，如果子代被支配，不更新Archive种群。如果Archive种群中存在个体被子代支配，从中随机挑选一个被子代替换。当Archive种群中的解与子代互为非支配解时，需考虑两种情况：(1) Archive种群数量小于N-1，此时直接将子代保留到Archive中。(2) Archive种群数量大于N-1，此时引入截断机制替换Archive中的解。这样可以保证种群大小为一个固定值。

Step7判断终止条件。本文的终止条件是进化次数t=MAXGEN。如果未满足条件则返回到Step 4,否则终止条件。

一直以来，林语堂始终坚持充分肯定女性的生命存在和人生价值，他呼吁：“我愿意看见新时代的女子，——她要无愧的标立、表现、发挥女性的不同，建造新女性于别个的女性之上。”[2]150可见，他的女性观是进步的，是符合时代潮流的。作者将木兰作为贯穿小说的中心人物，既赋予她超凡脱俗的气质和才华，又使她扮演着贤妻良母的传统角色，把经过其文化道德筛选的全部女性美揉合于他的女主人公木兰一身,使木兰达到形体美、心灵美、人性美的高度统一，继而升华到理想美的境界。[3]

Step8输出最终解集，算法结束。

4 性能评价指标及测试问题

4.1 评价指标

为了更好地分析算法的性能，本文采用的评价指标为反向世代距离(IGD)[14]。IGD作为综合评价指标，通过计算Pareto面到种群的距离的平均值来判断种群的分布性和收敛性。其计算公式表示为:

(4)

式中：P为最终种群；|P*|为Pareto面上参考点集P*的数量；d(x*,P)为参考点x*到离种群中各个解的最小距离。由式(4)可知，当IGD值越小时，种群的性能越好。

4.2 测试问题

本文选择了8个具有代表性的测试问题[15-16]来验证算法的性能，分别为：

1) 规整简单型Pareto面问题：DTLZ1、DTLZ2以及凸面DTLZ2(CDTLZ2)；

2) 倒转Pareto面问题：IDTLZ1、IDTLZ2；

3) 非连续问题：DTLZ7；

5) 目标范围不一致问题：SDTLZ2。

本文还对IGD数据进行了显著性比较[17]，其中+、-、=分别表示比PETA显著好、显著差以及没有显著区别。

5 实验结果

本文挑选了3种具有代表性的多目标优化算法(ε-MOEA[8]、NSGA-II[7]以及PESA-II[18])进行对比实验，得到的3维优化问题的最终解集。其中为稳态算法，在进化种群中采用Pareto支配维持进化种群的收敛性，在归档集中采用ε-支配维持归档集种群的收敛和分布性。ε-MOEA最终目的是要获得一组良好性能的归档集种群。NSGA-II采用非支配排序策略将种群划分为若干个非支配层，再根据层序将父代个体逐层保留到下一代，当保留下来的个体大于种群大小时，则在当前非支配层(临界层)中挑选部分个体保留下来。NSGA-II在临界层中采用聚集距离维持算法的分布性，从该层中挑选分布性好的个体保留下来。SPEA-II是在PESA[19]基础上的改进，它将目标空间划分为若干个超网格，PESA-II的过程包括选择超网格以及在该网格中随机选择一个个体保留。

图4给出了PTEA与其他3种算法在3目标DTLZ1测试问题上的最终解集。从直观上说，PTEA和ε-MOEA的分布性表现得最好，然而ε-MOEA很难搜索到Pareto面的边界。 通过图4可以看出ε-MOEA的广泛性没有PTEA的好。而其他两个算法的最终解集的分布明显不如前面的两个算法。

(a) PTEA (b) ε-MOEA

(c) NSGA-II (d) PESA-II图4 各算法在3目标DTLZ1测试问题上的最终解集

图5给出的是各算法在3目标DTLZ2测试问题上的最终解集，不管是均匀性，还是广泛性，PTEA的表现都要优于其他3种算法。PTEA的解集均匀地覆盖了整个Pareto面。而对于其他3种算法来说，ε-MOEA和PESA-II的性能差不多，都要好于NSGA-II。NSGA-II的解集虽然能够广泛地分布在Pareto面上，但是它的均匀性不是很理想。

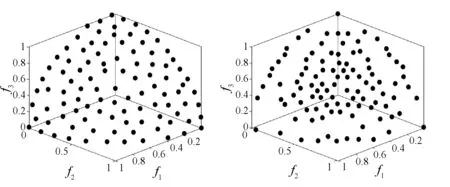
(a) PTEA (b) ε-MOEA

(c) NSGA-II (d) PESA-II图5 各算法在3目标DTLZ2测试问题上的最终解集

在降维问题上，如图6所示，PTEA已经覆盖到了整个Pareto面，而在Pareto面的两端解的分布明显稀疏与中间部分。而其他两个算法同样有小部分区域没有解的分布。比如图6(c)的Pareto面的上半部分区域以及图6(d)的Pareto面的上半部分和中部区域相对来说都比较稀疏。

(a) PTEA (b) ε-MOEA

(c) NSGA-II (d) PESA-II图6 各算法在3目标DTLZ5测试问题上的最终解集

图7给出了4种算法在非连续问题(DTLZ7)的优化结果，该问题的Pareto面由4个区域组成。可以发现，ε-MOEA的分布性要稍好于PTEA，但是广泛性没有本文算法好。在DTLZ7问题上，本文算法的分布性与NSGA-II和PESA-II没有太大的区别。

(a) PTEA (b) ε-MOEA

(c) NSGA-II (d) PESA-II图7 各算法在3目标DTLZ7测试问题上的最终解集

对于CDTLZ1测试问题，它是DTLZ1测试问题的变体，其Pareto面为凸面。如图8所示，表现最好的是PTEA，其次是PESA-II。虽然ε-MOEA的解集看似均匀分布，但它没有搜索到整个Pareto面，而是大部分解集都聚集到了Pareto面的中部位置。而与ε-MOEA的解集分布相反的是NSGA-II的大部分解集聚集在了Pareto面的边界。

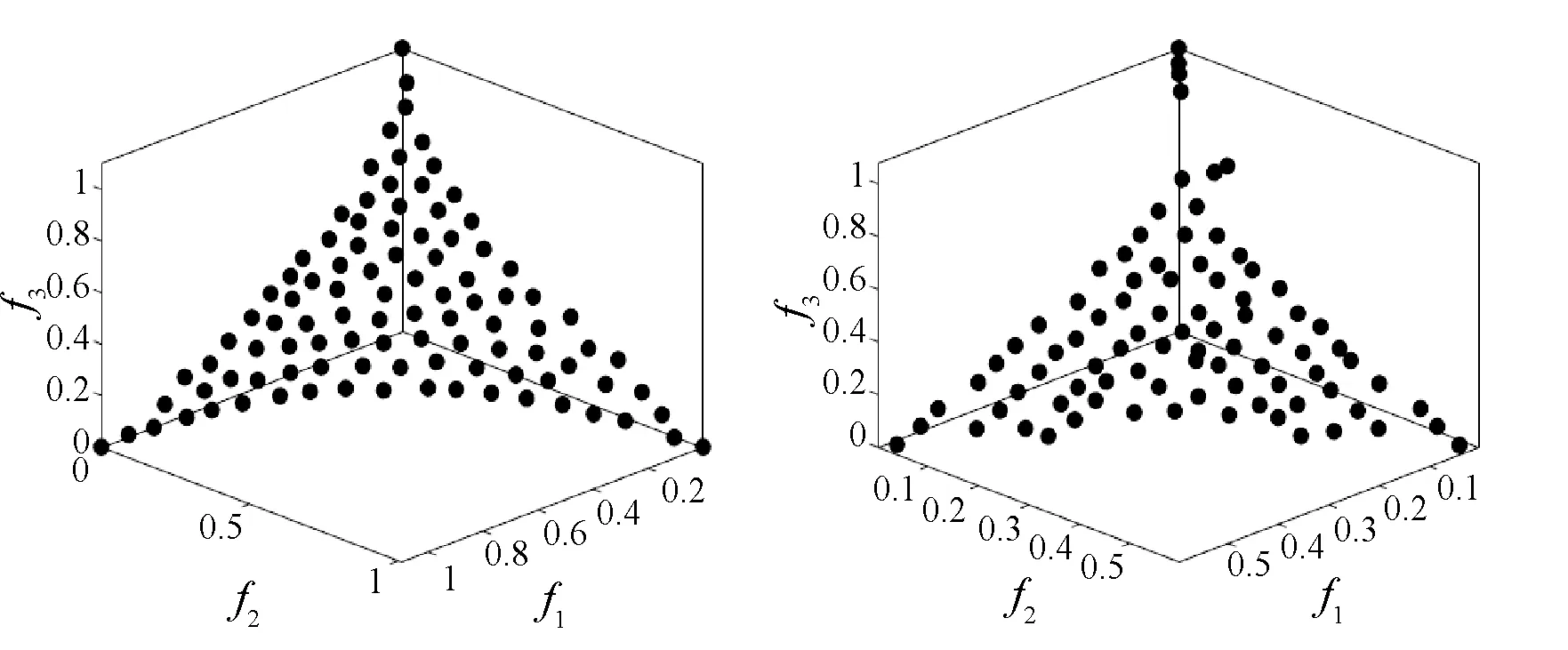
(a) PTEA (b) ε-MOEA

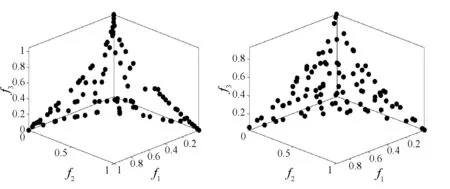
(c) NSGA-II (d) PESA-II图8 各算法在3目标CDTLZ1测试问题上的最终解集

图9和图10给出了各算法在倒转Pareto面问题上的解集分布，在这两个问题上，PTEA的性能同样也是最好的。

(a) PTEA (b) ε-MOEA

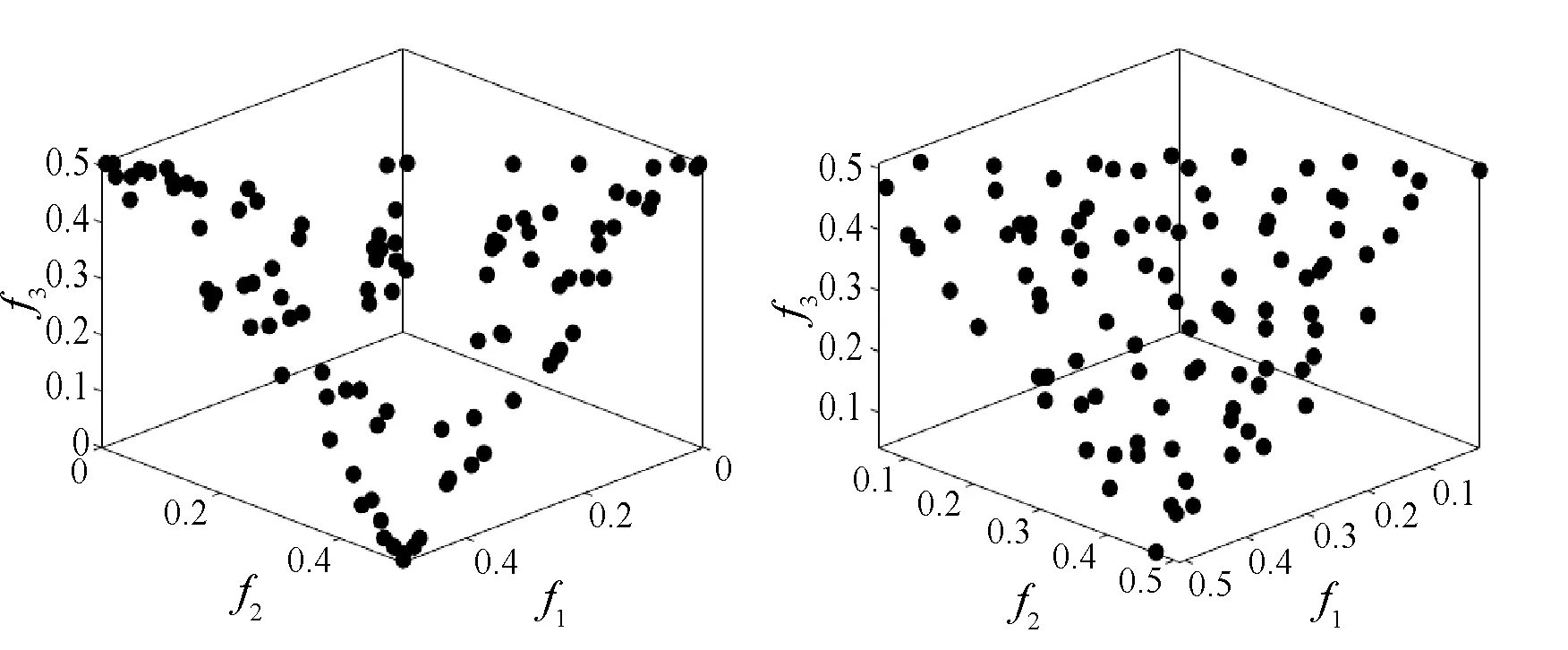
(c) NSGA-II (d) PESA-II图9 各算法在3目标IDTLZ1测试问题上的最终解集

(a) PTEA (b) ε-MOEA

(c) NSGA-II (d) PESA-II图10 各算法在3目标IDTLZ2测试问题上的最终解集

最后是SDTLZ1问题，该问题的各个目标的取值范围都不相同，本文将各个维度i的取值范围设置为[0,2i]。从图11中解集的分布可以看出，PTEA和ε-MOEA的分布最均匀，而4种算法的分布广泛性相当。

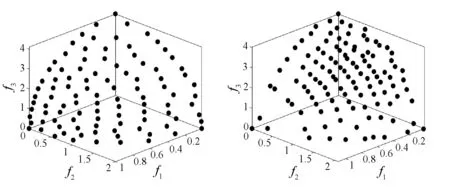
(a) PTEA (b) ε-MOEA

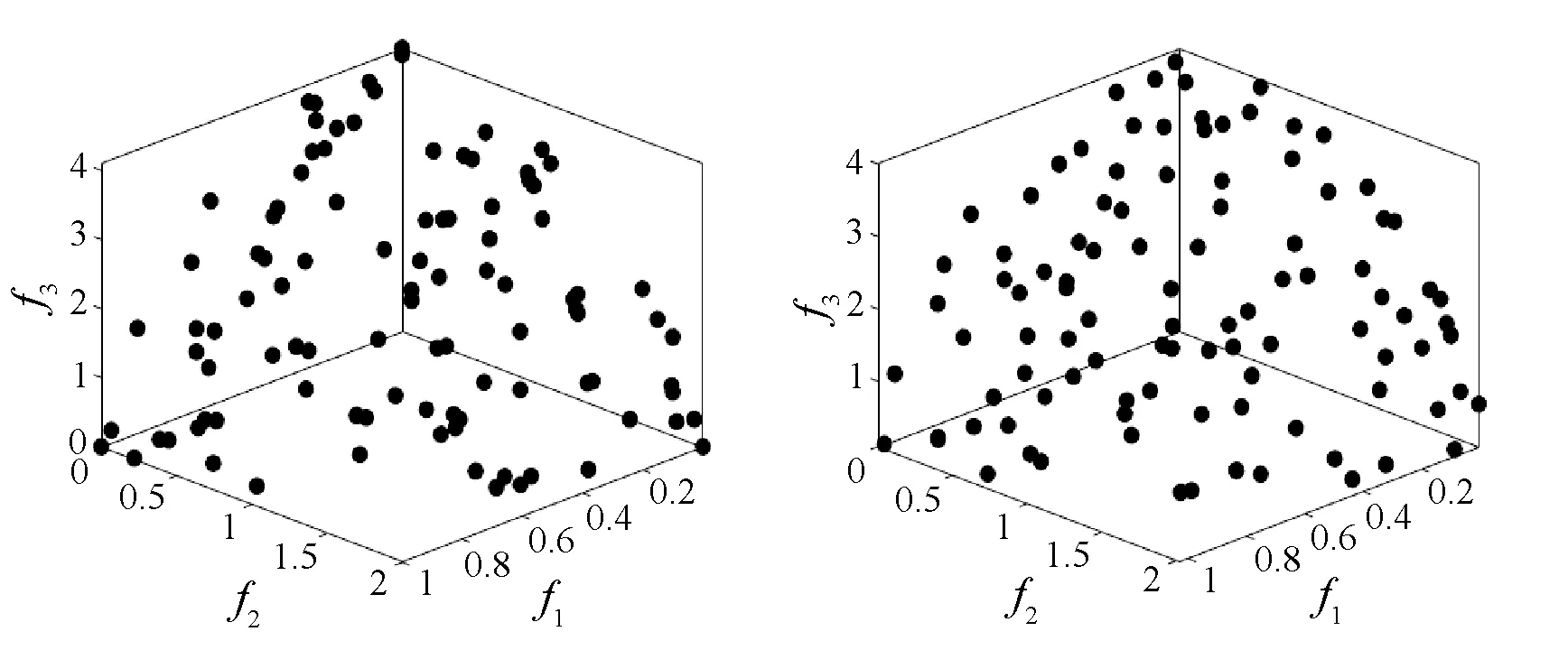
(c) NSGA-II (d) PESA-II图11 各算法在3目标SDTLZ2测试问题上的最终解集

因此，从分布均匀以及分布广度两个角度观察，本文算法都要优于其他3种算法。同时，本文算法避免了额外的参数设置，极大提高了算法的实用性。

本文除了从直观上体现算法性能外，还给出了定量分析。如表1给出了4种算法在不同测试函数上综合性能的数据结果，表中的数据为算法运行30次统计得到的IGD平均值。 表1中的A、B、C、D、E、F、G、H分别表示DTLZ1、DTLZ2、DTLZ5、DTLZ7、CDTLZ2、IDTLZ1、IDTLZ2、SDTLZ2测试问题。

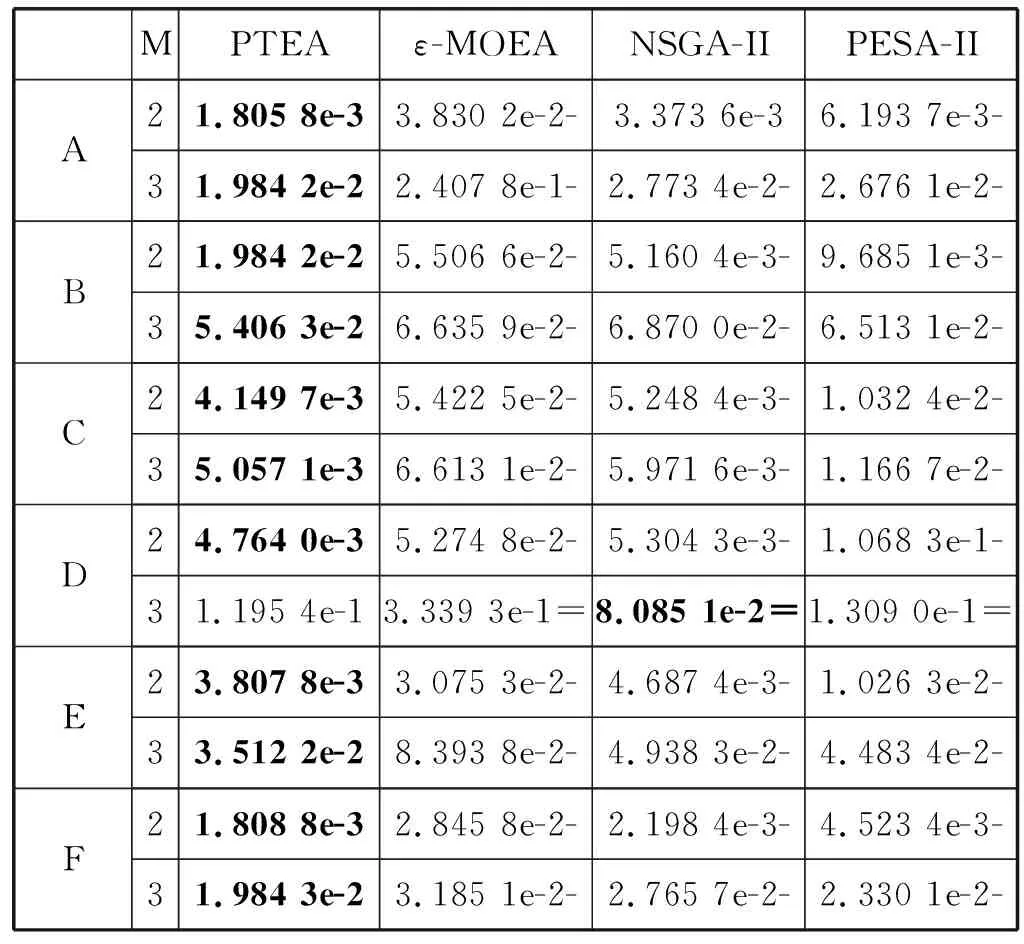
表1 算法在各个测试问题上的IGD值

续表1

从表1中可以看出，总共16个测试问题，PTEA有14个表现得最好，仅3维的DTLZ7和3维的SDTLZ2分别稍差于NSGA-II和ε-MOEA算法。而就显著性而言，本文算法有14个测试问题显著优于ε-MOEA，15个测试问题显著优于NSGA-II和PESA-II。

6 结 语

本文针对稳态多目标优化算法，提出了一种基于截断机制的稳态优化算法(PTEA)。本文还通过一系列对比实验验证了该算法的性能。从算法的最终解集的分布以及IGD统计数据可以发现，PTEA能有效地平衡种群的分布性和收敛性。

虽然PTEA能够很好地优化2～3维的优化问题，但是它很难在高维优化问题上获得良好的解集。其主要原因是PTEA依赖Pareto支配机制引导种群收敛，而Pareto支配随着维度的增加其作用将急剧减弱。因此，引入一种新的收敛机制将是后续的研究方向。