基于平滑渐进l1范数的压缩感知信号的重构算法

陈 暄 潘春平 龙 丹

1(浙江工业职业技术学院 浙江 绍兴 312000)2(浙江大学 浙江 杭州 310058)

0 引 言

随着无线传感网中技术的快速发展，早期使用Nyquist处理信号的方法由于其存在效率低、资源消耗高和硬件成本昂贵等缺点已经被放弃[1-2]。压缩感知CS(Compressed Sensing)[3-5]理论能够采用远低于Nyquist采样条件，使用随机方法获得离散样本。该理论已经广泛地使用在信息论、地球科学、无线通信和模式识别等领域。CS中的信号重构是恢复原始信号的关键。目前常见的信号重构算法主要分为基于l1范数的最小凸优化算法和基于l0范数最小的贪婪算法。前者计算量比较庞大,但重建效果好,其代表有：基追踪法BP(Basis Pursuit)[6]、梯度投影法GPSR(Gradient Projection For Sparse)[7]、凸集交替投影法POCS(Projection Onto Convex Sets)[8]、同伦算法HA(Homotopy Algorithm)[9]和最小角度回归法LARS(Least Angle Regression)[10]等。后者具有精度差、计算速度快的特点,其代表有：匹配追踪法MP(Matching Pursuit)[11]、正交匹配追踪法OMP(Orthogonal Matching Pursuit)[12]、分段正交匹配追踪法STOMP(Stagewise Orthogonal Orthogonal Matching Pursuit)[13]等。文献[14]提出基于平滑l0范数的压缩感知平面近场声全息法,实验说明算法具有较好的效果，但存在需要在感知矩阵、全息面测量声压和稀疏向量共同构成的约束条件下才能建立模型的问题，提高了计算量。文献[15]提出采用新的近似l0范数的函数,并结合牛顿算法实现图像重构，取得了较好的效果，但是没有对采用简单的分式函数近似估计l0范数进行证明。文献[16]在分块图像中使用l1范数来估计混合高斯脉冲噪声，取得了较好的结果，但提高了算法复杂度，去躁效果不明显。文献[17]提出在l1范数中的基于柔化神经网络的低秩矩阵分解方法,该方法能够有效降低噪声比，但算法消耗了更多的时间。文献[18]提出了基于l1和l2范数的稀疏重构算法用于稀疏模型重构，取得的较好的效果，但没有与其他重构算法进行比较，实验结果稍显不足。文献[19]提出了基于l1范数的图像分辨算法，提高了图像清晰度，但增加了算法的复杂度。

综上所述，压缩传感中信号重构最理想的方法是采用基于最小l0范数的重构,这是一个NP问题。因此转换为求解l1最小范数问题来进行解决,但是由于最小l1范数并不是可导的,影响重构的效果。本文构造了基于l1范数的光滑逼近函数,重点分析和证明了该逼近函数的单调性和最优解序列的收敛性。最后通过该平滑渐进近函数求解信号重构问题。

1 预备知识

一般来说，求解压缩传感的信号重构的时候,采用求解最小的l0范数问题,思路如下:

(1)

s.t.Ax=y

文献[20-21]证明了基于最小的l0范数进行信号重构等价于使用求解最小l1范数的信号重构。因此通常采用求解最小l1范数问题去解决信号重构的问题,因此模型如下:

(2)

s.t.Ax=y

显然,式(2)是一个凸规划问题[22]。虽然可以转换为线性规划问题，但存在求解过程规模扩大，造成计算速度慢，重构效果差的问题。

2 基于平滑渐进的l1范数信号重构算法研究

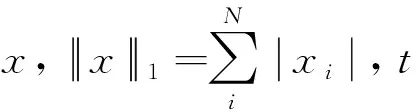
定义1当x∈RN,t>0,则:

(3)

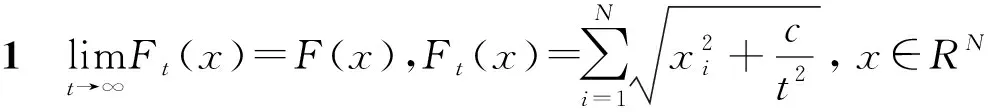
证明过程如下:

(4)

对于任意的x和t而言：

(5)

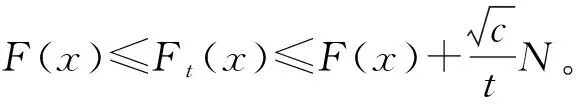
因为：

F(x)+0=F(x)

(6)

式(6)化简为:

(7)

证明完毕。

通过定理1可以将式(1)改写为如下:

minFt(x)

(8)

s.t.Ax=y(t→+∞)

当具有连续的实数时,式(5)的求解非常难。可以通过离散化t得到:

minFt(x)

(9)

s.t.Ax=y(tk→+∞)

能够求解该公式是否成立，是本文所需要描述的主要对象。

定理2存在集合S={x|Ft(x)≤Fk(x)}具有一定的界限,当x*(tk)是t=tk时,式(9)获得最优解,所以x*就是式(1)的最优解,因此在{x*(tk)}中存在子序列收敛于x*。

证明如下：

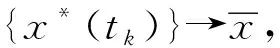
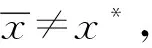
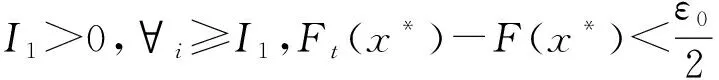
因此得到：

(10)

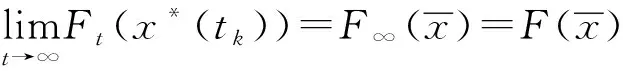
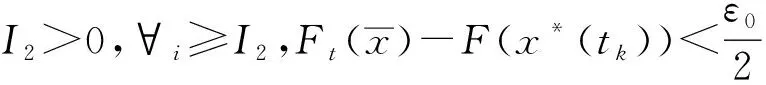
所以,对于∀i≥max{I1,I2}存在:

(11)

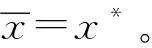
定理3式(9)是一个凸规划问题。

证明如下:假设集合D={x|Ax=y},其中,A是一个N×M矩阵,x∈RN,y∈RM对于∀x(1),x(2)∈D并且∀λ∈[0,1]

A[λx(1)+(1-λ)x(2)]=λAx(1)+(1-λ)Ax(2)=

λy+(1-λ)y=y

(12)

因此,λx(1)+(1+λ)x(2)∈D

所以,D是一个凸问题。

因为:

Ft(x)+▽Ft(x)TΔx

(13)

所以,Ft(x)在D上是凸函数,而实际上：

RN×M是一个正定矩阵。

所以,Ft(x) 在D上是严格凸函数,证明完毕。

定理4假设x*(tk)是t=tk的式(1)的最优解,x*是式(2)的全局最优解,因此,对于任何一个tk>0且k→+∞,则有:

(14)

证明:选择目标函数Ft(x)在x=x*(tk)处的泰勒展开为:

Ft(x)=Ft(x*(tk))+▽Ft(x*(tk))T(x-x*(tk))+

▽Ft(x*(tk))(x-x*(tk))+

o(x-x*(tk))T(x-x*(tk))

(15)

令x=x*,同时结合一阶求导必要条件,得到:

o(x-x*(tk))T(x-x*(tk))

(16)

因为▽2Ft(x)为对角矩阵,因此得到:

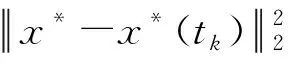
(17)

又因为Ft(x)关于t进行单调递减,因此得到Ft(x*(tk))-Ft+1(x*(tk))<0,由于x*是式(2)的全局最优解,因此得到Ft(x)-Ft(x*(tk))<0。

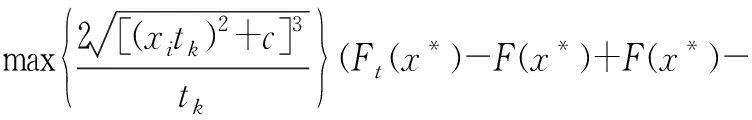
F(x*(tk)+F(x*(tk)-Ft(x*(tk)))≤

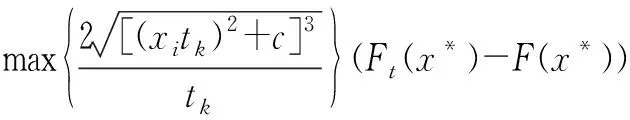
(18)

证明完毕。

综上所述，根据定理2,求解式(9)的算法如下:

步骤1输入矩阵A和t0,测量值y,阈值ε为10-6,步长h；

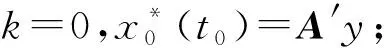
步骤3令tk=t0+kh,求解式(9)的最优解x*(tk)；

3 实验说明

3.1 算法实例说明及重构效果对比

设定：

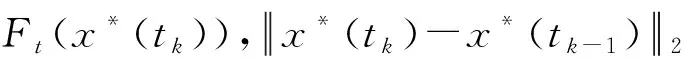
表1 数值结果

续表1

表2 数值结果

图1 原始信号

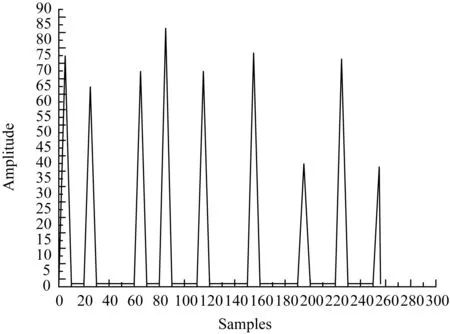
图2 频域信号

图3 本文算法重构

3.2 本文算法与其他重构算法的对比

3.2.1 经典的压缩算法对比

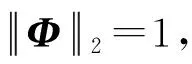
图4 运行时间对比

图5 迭代次数对比

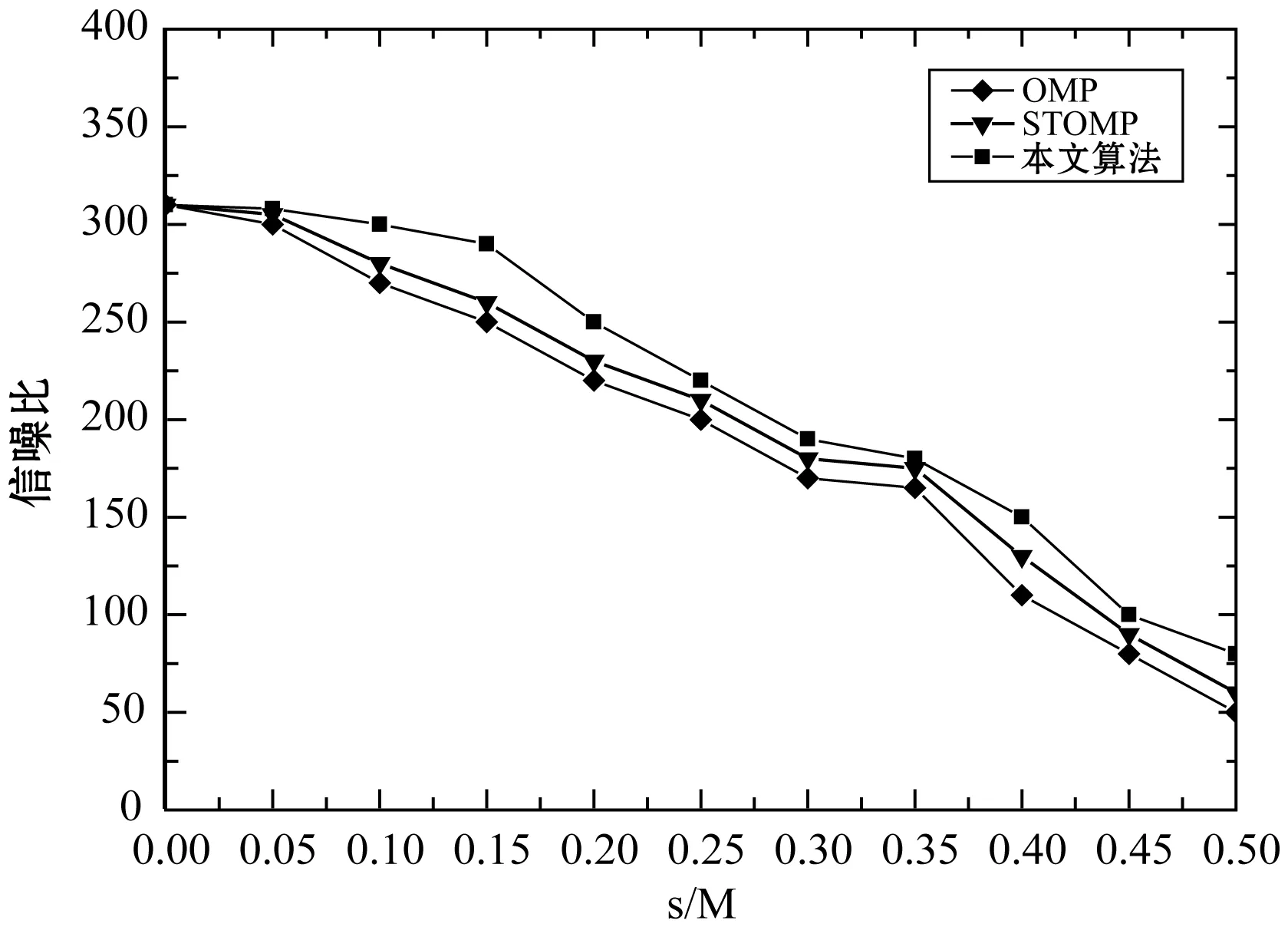
图6 信躁比对比

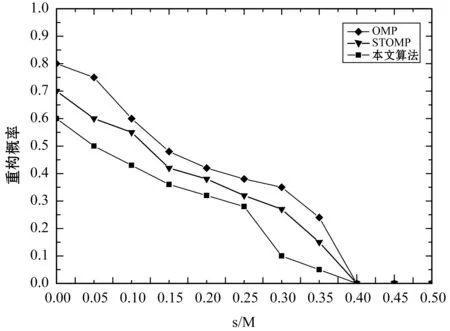
图7 重构概率对比

3.2.2 与l1范数算法比较

为了进一步验证本文算法的性能,将本文算法和最新的几种关于l1范数算法(算法所需要的参数遵循各自文献中的参数)进行对比, 在统一的压缩比下，比较效果如图8所示。在图8(a)中可以发现，本文算法率先完成图像信号的匹配度,这说明本文算法的性能确实有了很大的提高。(b)中发现，本文算法的相对误差明显小于其他3种算法,这说明算法的自身的精度高,降低了误差比例。(c)的PSNR的值是4种算法中最高的,进一步说明了本文算法的重构效率是良好的。从(d)中的运行时间来看,4种算法的运行时间都有不同程度的增加,但从整体上看本文算法的运行时间要稍微优于其他3种算法。

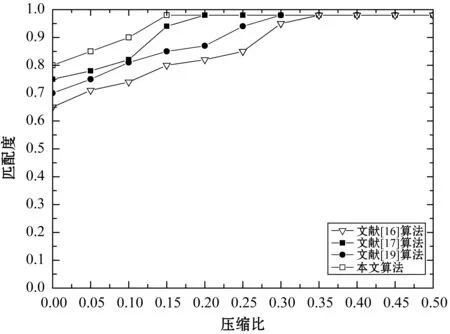
(a) 匹配度比较

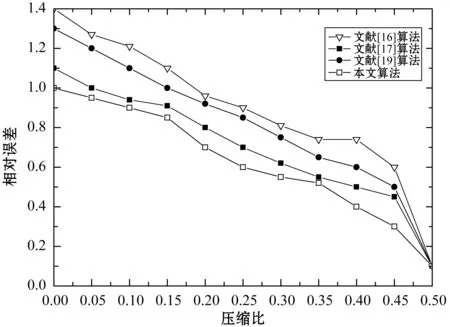
(b) 相对误差比较

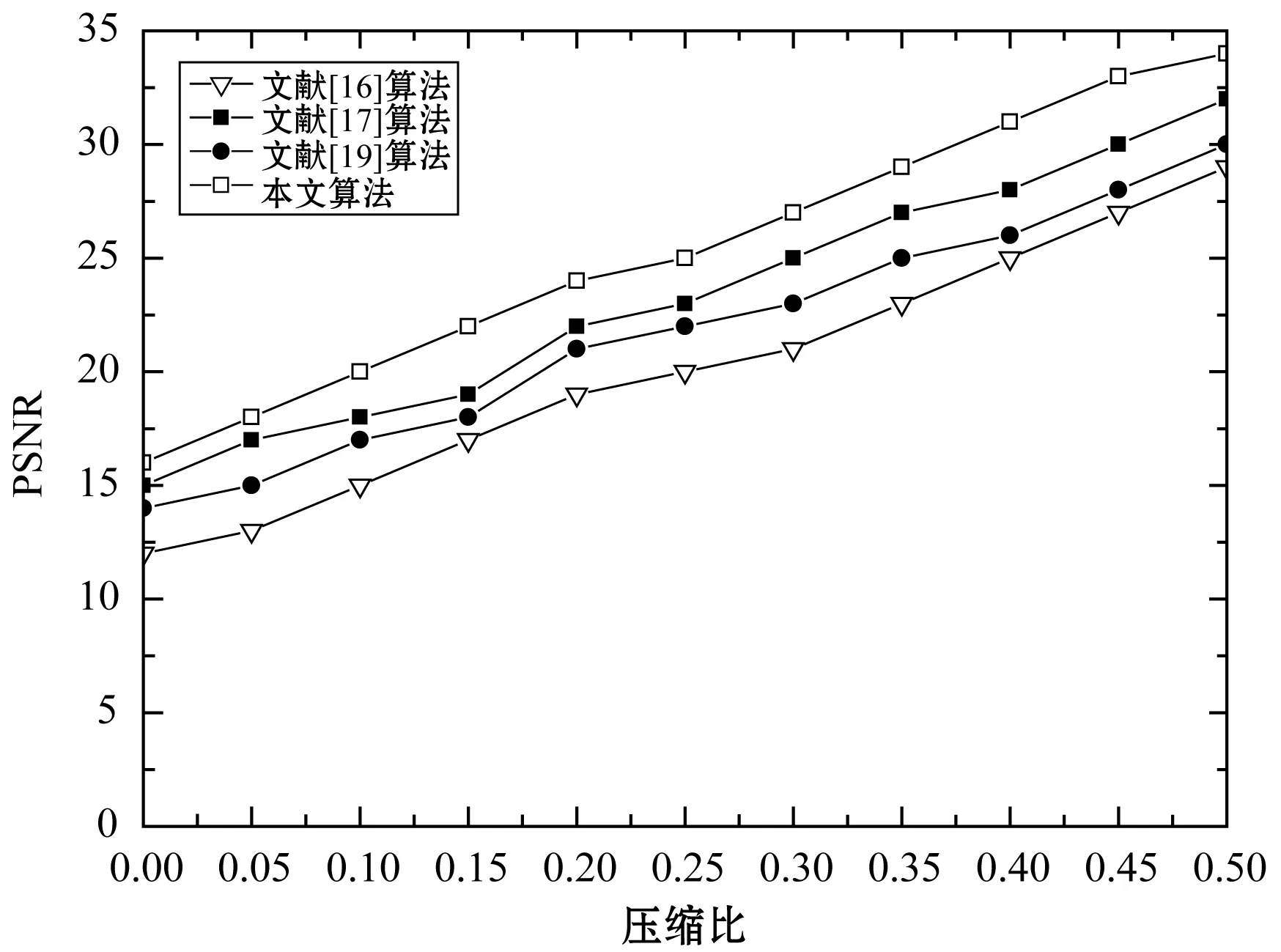
(c) 峰值信躁比PSNR比较

(d) 运行时间比较图8 4种算法对比效果比较

4 结 语

针对最小l1范数不可导的问题,提出并构造了基于平滑渐进的l1范数函数。通过一系列证明推理说明该函数具有渐近的单调性和最优解序列收敛性,从而进一步说明了本文算法能够在一定程度改进信号重构效果。