基于ARIMA与自适应过滤法的组合预测模型研究

徐 超 项 薇 季孟忠 谢 勇

(宁波大学机械工程与力学学院 浙江 宁波 315211)

0 引 言

时间序列预测是预测领域中的一个重要分支，它是收集和分析过去在不同时间的历史观察数据，寻找和描述其基础关系，并推广到未来的模型。时间序列预测已被广泛应用于众多领域问题的预测中，如金融领域[1]中股票市场预测[2]、医疗领域[3]传染病发病率的预测[4-5]等。

国内外学者开展了大量相关研究工作。文献[6]汇总整理了若干预测方法和数学模型，用于不同类型时间序列问题的预测。其中，自回归综合移动平均(ARIMA)模型[7]是最广泛使用的时间序列模型之一。该模型对所有历史时间序列数据进行客观分析，识别数据中的季节性和趋势性特征，然后进行预测。它以短期预测精度高而广受研究者的青睐[8]。如周奎[9]根据1978年-2007年的GDP数据建立了ARIMA(2，1，6)模型，对2008年-2013年的GDP进行预测，预测误差均在5%以内。Abdur Rahman等[10]利用1972年-2015年44年的时间序列数据建立二氧化碳排放模型，发现ARIMA(0,2,1)为最佳拟合模型并预测2016年-2018年二氧化碳排放量，结果都在95%的置信区间。在时间序列预测中还有一种方法就是平滑预测法，它的特点是首先对时间序列数据进行平滑处理，过滤由偶然因素而引起的波动，然后再找出其规律，如移动平均法、指数平滑法[11]、自适应过滤法。其中移动平均法和指数平滑法的优点就是建模过程简便，缺点是当计算移动平均值时，只利用时间序列的前N个数据，没有充分利用时间序列的全部数据信息，也不能识别时间序列数据之间的内部关系，所以这并非一种理想的预测方法[8]。自适应过滤法是在移动平均法的基础之上，根据数学上最优化原理，对移动平均模型中的权数进行调整，以减小预测误差[12]。该方法在经济领域和工程检测应用比较普遍，如股票走势、期货行情等的预测[13]。虽然该方法可以减小预测误差，但也没有充分利用时间序列数据中的所有信息，所以在实际应用中有些复杂系统的预测中，只能做到一些趋势的预测，如陶庭叶等[14]应用自适应过滤法模型预测大坝变形趋势。

综上述，ARIMA模型的优点是可以充分利用所有时间序列数据，识别数据内部关系中季节性和趋势性的预测。但其只有在短期预测时精度高，而长期预测精度较小。自适应过滤法可以通过调整权数以减小预测误差从而提高预测精度。本文提出将ARIMA模型和自适应过滤法相结合，提高短期预测和长期预测(即增加预测步长)的预测精度。

1 ARIMA、自适应过滤法和组合预测法

1.1 ARIMA模型

ARIMA模型形式是ARIMA(p,d,q)，它是针对非平稳时间序列数据进行预测建模的一套方法。其一般表达式为：

xt=φ0+φ1xt-1+…+φpxt-p+εt-θ1ε1-

…-εqεt-q

(1)

即在t时刻时间序列的取值xt是前p期历史数据xt-1,xt-2,…,xt-p和前q期预测误差εt-1,εt-2,…,εt-q的多元线性函数，误差项是当期的随机干扰εt，为零均值白噪声序列。

其建模过程分为四个步骤：

① 时间序列的平稳化：ARIMA模型只能应用于平稳的时间序列数据中，而该模型序列平稳化的方法是将数据进行差分,其中d是差分的次数。

② ARIMA模型的识别：也叫模型的定阶，即确定p与q，主要是根据模型的自相关系数(ACF)和偏自相关系数(PACF)的性质，选择合适的模型。

③ 模型参数估计以及模型验证：对ARIMA模型进行参数估计，通常采用最小二乘法或极大适然法进行参数估计。同时验证模型，不合适则返回第2步，重新识别模型。

④ 模型的应用：通过滚动的单步预测计算实现短期预测。

1.2 自适应过滤法

自适应过滤法是以时间序列的历史观察值的加权平均来预测的，关键在于确定一组“最佳”权数。其核心思路是根据预测误差反馈调整权数，反复迭代直到找出一组“最佳”权数使误差最小。自适应过滤法预测模型的一般表达式如下：

(2)

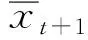
② 计算实际值与预测值之间的误差：

(3)

③ 由误差ei+1的大小来调整权重的大小，使其预测误差减小。调整权重的公式是：

(4)

(5)

式中：分母代表的意义是历史时间序列数据中N个观察值的平方和最大值。好的k值不仅可以减少迭代次数，还可以确保误差值最小。

这样反复迭代调整权重，直到找到一组“最佳”权重，使误差减到最小。从t=N到t=M称之为一轮迭代。然后将一轮迭代所得到的最后一组权数作为初始权重进行下一轮迭代。这样反复迭代直至误差无法改进为止，即为一组“最佳”权重。后续预测采用这组“最佳”权重。

自适应过滤法有两个优点:(1) 技术简单，可以依据研究者的需要来选择“权重”的个数和学习常数k，从而控制预测。(2) 该方法利用所有时间序列的观察值来寻找“最佳”权重，而且是随着历史数据的轨迹变化不断更新权重，使得预测更加精准。并且自适应过滤法中“权重”的特点是任意的，完全突破了一切约束，即经过调整后得到的权重之和不但可以不等于1，而且还可以为负数。

1.3 ARIMA-自适应过滤组合预测模型

根据上文所叙述，在传统的ARIMA建模过程中，其特点是对于短期预测精度较高。而随着预测步长的增加，ARIMA模型的预测误差加大，而自适应过滤法是以减小预测误差为目的，经过层层迭代来调整“参数”的思想。将这两种方法结合，使得短期预测的精度比传统的ARIMA模型更高。同时，当预测步长较大时，也可以保持较高的预测精度。

传统的ARIMA建模过程中，其中一个步骤是对模型参数的估计，即对式(1)中φ1,φ2,…,φp,θ1,θ2,…,θq进行估计，而式(1)可以看成一种加权多项式。根据自适应过滤法中“权数”的特点，将φ1,φ2,…,φp,θ1,θ2,…,θq看成式中变量的“权数”。在ARIMA建模的第3个步骤后，我们将自适应过滤法的思想嵌入其中，即将估计出来的参数φ1,φ2,…,φp,θ1,θ2,…,θq当作初始权值。用自适应过滤法进行参数的调整，使其预测误差尽可能的减小，得到一组“最佳”的参数返回ARIMA模型中，然后进行预测。该模型通过计算机编程实现，在程序设计中采用传统的ARIMA预测结果的最小绝对误差(MAE)来度量。该组合预测法建模的流程如图1所示。

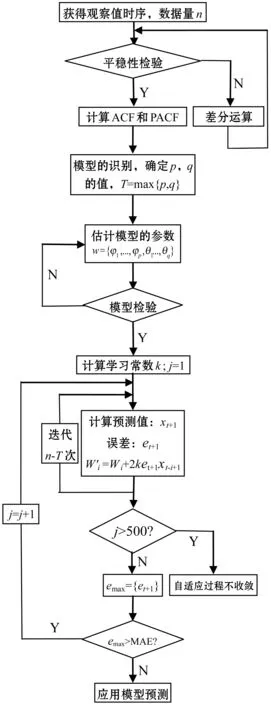
图1 ARIMA与自适应过滤组合预测法流程图

2 算例比较分析

2.1 算例选取

为了评价组合预测法的适用范围及预测精度，考虑选取不同类型的时间序列数据进行预测评价。比较的模型是：ARIMA模型和ARIMA-自适应过滤组合模型(以下简称组合模型)。所有时间序列的算例均来自澳大利亚Monash大学的Rob Hyndman教授创建的TSDL。

时间序列数据有多种分类，按照时间序列平稳性特征可分为：平稳时间序列和非平稳时间序列。平稳时间序列即为均值和标准差没有随系统的变化而变化，且严格消除周期性变化的时间序列；非平稳时间序列即为均值和标准差等数字特征随时间的变化而变化呈现某一种趋势的时间序列，比如周期性(季节性)、上升(下降)趋势。而在实际的应用中所获得的时间序列通常为非平稳时间序列。

本文在TSDL中选取的总共13组不同领域规模的时间序列数据(见表1)，归类出四类特征：1) 平稳时间序列；2) 既有周期性又有趋势性；3) 仅有上升趋势；4) 仅有下降趋势。在既有周期性又有趋势性特征的时间序列主要选取两种类型：一类是随时间的推移，一个周期内数据波动的幅度不变(如Wisconsin employment time serie，时间序列图如图2所示)；另一类是一个周期内数据的波动幅度随时间的推移而变化(如Monthly production of Gas in Australia，时序图如图3所示)。在仅有上升或下降趋势特征的时间序列数据中，我们也主要选取两种类型的数据：一类是数据上升或下降趋势中没有波动或者波动幅度可以忽略不计；另一种类型是数据在上升或下降趋势中有波动的情况。这样我们选取的数据类型几乎涵盖实际应用中的大部分情况。

表1 算例分类和算例数据量

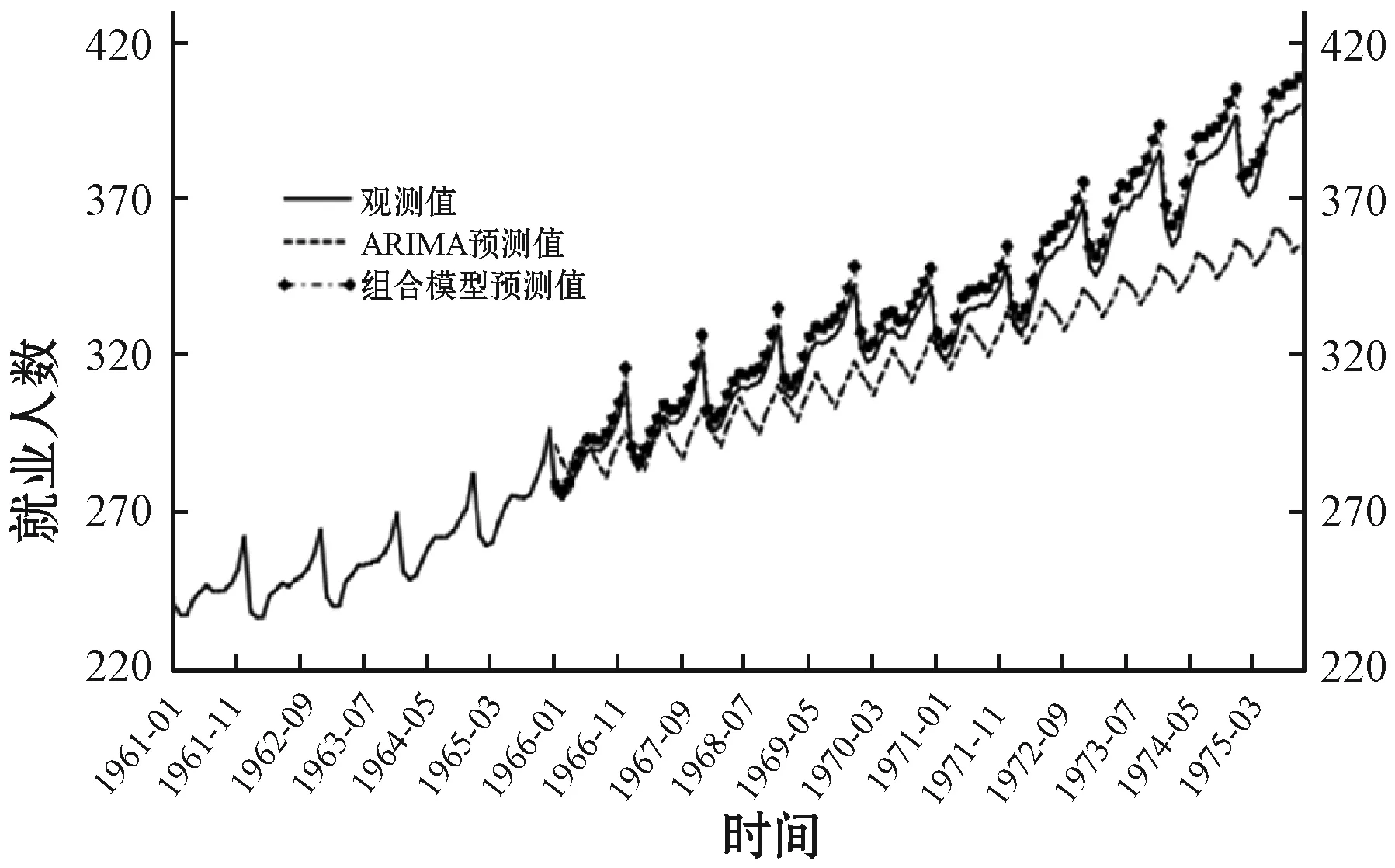
图2 1962年—1975年月均就业人数观测值与预测值的时序图

图3 1956年—1994年汽油月均产量观测值与预测值时序图

2.2 算例实验设计和计算

算例评价中，本文关注模型的预测精度。预测精度的评价一方面采用从短期预测结果的相对误差(PE)的最大值和最小值、平均绝对百分比误差(MAPE)和相对误差的标准差四个指标来比较。其中：最大值和最小值表示预测精度的极限情况；MAPE表示预测精度；相对误差的标准差表示预测精度的变化情况。另一方面从长期预测的角度，即增加预测步长，从预测结果MAPE的变化率比较。

我们使用MATLAB R2014a进行编程建模。本文实验设计的思路是将所有的时间序列历史数据分为两部分，前一部分成为观测组，后一部分为验证组。用观测组的数据作为新的时间序列历史数据预测后面的数据，将预测值与验证组的真实值比较，计算出预测值的相对误差(PE)([PE=(真实值-预测值)/真实值]×100%)。算例的分类和数据量的大小如表1所示。

2.3 对比结果

通过MATLAB仿真，分别应用ARIMA模型和组合预测模型对这13组数据预测，并计算两个模型所得各预测值的相对误差(PE)，提取和计算出PE中的最大、最小值和平均绝对百分比误差(MAPE)，以及PE的标准差的值，其结果如表2所示和表3所示。表中“PEmax”和“PEmin”分别表示各组数据预测值相对误差的最大值、最小值，σPE表示PE的标准差。

表2 ARIMA模型预测值相对误差

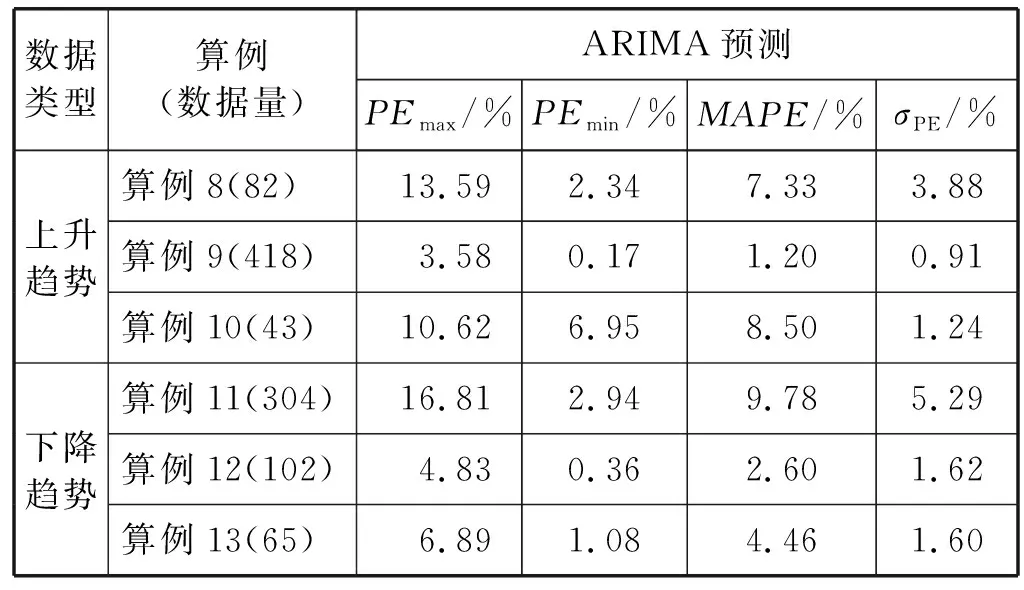
续表2

表3 ARIMA-自适应过滤组合模型预测值相对误差

比较表2和表3可知，对于短期预测，从预测值相对误差(PE)角度来看，平稳时间序列应用ARIMA模型的预测精度比较小。从表中数据可看出，ARIMA模型对平稳时间序列的预测的MAPE在10%～30%之间；而非平稳时间序列的应用ARIMA模型的预测精度相对较高，预测的MAPE在90%～95%之间。本文提出的组合预测模型不论什么特征的时间序列数据，预测精度都在97%以上，甚至接近真实值(如算例3、算例4、算例8)。针对相对误差的标准差这一指标，我们发现，时间序列样本数据量较小时(如算例10和算例13)，应用组合预测模型的σPE值大于ARIMA模型的该项指标；其余算例(数据量较大)，组合预测模型预测的σPE指标都较之ARIMA模型的小。结合图1和图2，两种模型所预测的结果与观察值趋势对比，说明本文提出的组合预测模型的结果较ARIMA模型细致，更加接近实际情况。

对于长期预测(即增加预测步长)角度来看，由图2和图3可看出，随着预测步长的加长，ARIMA模型虽然呈现出数据的变化趋势，但是预测精度却越来越小。本文提出的组合预测模型的预测精度却变化不大，图2对应的预测值的MAPE随预测步长的变化情况见图4。由图4可知，ARIMA模型的预测结果的MAPE随预测步长呈线性增加，且变化率较大；组合预测模型，预测步长在108个月内时，预测结果的MAPE几乎无变化，预测步长大于108月时，预测结果MAPE开始变大。

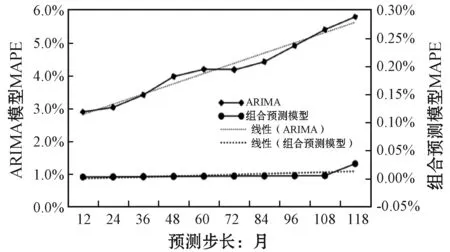
图4 预测步长与MAPE的变化图

3 结 语

本文提出一种将传统ARIMA模型与自适应过滤法相组合的组合预测模型。该模型以ARIMA模型为框架，加入自适应过滤法调整权数的思想，调整ARIMA模型中的参数，从而提高预测精度。本文分别从平稳时间序列、周期性+趋势性、上升趋势、下降趋势四个特征共13组时间序列算例对ARIMA模型和组合预测模型进行预测计算和比较。结果发现：对于短期预测，ARIMA-自适应过滤组合预测模型的预测精度趋势优于传统ARIMA模型，预测精度增大了80%～99%，并且预测出的未来趋势也更加接近实际情况。对于长期预测(即预测步长加长)，ARIMA模型预测结果平均绝对百分比误差(MAPE)变化率较大，组合预测模型预测结果平均绝对百分比误差变化率几乎为0。所以，本文提出的组合预测模型对平稳和非平稳时间序列的预测是有效的，并且也适用长期预测。本文的不足之处在于，在组合预测模型对参数的调整过程中，误差的收敛时间比较长，在接下来的研究中，可以从缩小收敛时间方面着手。