并行化遗传算法研究综述

冯智莉 易国洪,2 李普山 黎慧源 代 瑜

1(武汉工程大学计算机科学与工程学院 湖北 武汉 430205)2(武汉工程大学智能机器人湖北省重点实验室 湖北 武汉 430205)

0 引 言

人工智能领域中，一个非常关键的问题是需要在非常庞大并且十分复杂的解空间中找到最优解或者是近似最优解。对这种NP-hard问题[1]，不恰当的搜索方法可能会出现组合爆炸的问题[2]，因此找到一个通用的搜索算法一直都受到相关领域研究人员的关注。

最优化问题一般可以分成两类：组合优化问题和函数优化问题[3]。其中：函数优化问题即连续变量的优化问题，目标对象是指定区间的所有变量；而组合优化的目标对象则是在无限集中某一个符合要求的目标答案，如旅行商问题[4]TSP 。目前对于函数优化问题常见的解决策略是精确算法和智能优化算法。精确算法包括:整数规划[6]、动态规划[7]、线性规划算法[5]和分支定界[8-9]等，这些时间复杂性较大，适合用于小规模问题。智能优化算法主要包括文献[10]在1953年提出的模拟退火算法、文献[11]于1973年提出的遗传算法GA、文献[12-14]于1986年提出的禁忌算法、文献[15]于1992年提出的蚁群算法和文献[16]以革新的方式使用神经网络方法。其中，以遗传算法、模拟退火算法等为代表的指导性搜索法，以贪心算法[17]等算法为代表的局部搜索法，均借鉴了一些自然现象，以及人的思维活动来指导搜索活动的展开。遗传算法优势在于：可以快速地将解空间中的全体解搜索出，全局搜索能力优秀[18]，克服了其他算法的快速下降陷阱问题；适合分布式计算，天然并行性加快了收敛速度。但是相对的，遗传算法局部搜索能力不足，简单遗传算法耗时长，在进化后期搜索效率较低[19]，所以存在一定的早熟收敛的风险。遗传算法的难点是采用何种选择方法，在充分保留好的个体的同时，又要维持群体的多样性。

1 基本概念和主要环节讨论

遗传算法是诸多进化算法中的一种。模拟了自然界中生物自然淘汰的进化过程，学习不仅可以通过单个生物个体的适应来完成，还可以通过种群的进化来实现，并将其运用到计算机模型之中[20]。Darwin 进化论中适者生存的原理认为，每一代种群最终都会越来越适应环境。每一个个体都会继承但不完全继承父辈的特性，自身会随机的产生一些新特性，只有高度适应环境的个体才能被保留下来。遗传算法从代表问题中生成一个或多个初代解集(种群)，解集中的解又被称之为个体，个体本质上是带有特征的实体，经过基因编码来实现。经过适应函数筛选的个体形成的新的种群，遗传算法不断地评价每一个个体，保证更适应环境的个体拥有更多的繁殖机会。遗传算法放弃了梯度信息，重视的是种群之间的搜索策略，以及个体信息在种群内的交换，克服了传统搜索算法难以解决非线性复杂问题的缺点，具有适合并行处理、鲁棒性强、简单通用、搜索能力强和运用范围广的特点[20]。目前已经广泛地运用在自适应控制、机器学习、组合优化、人工生命等领域。

在遗传算法中，问题的解(表现型)所组成的群体(种群)会朝着更加适应环境的方向变化。每个候选解都有一组属性(个体染色的编码信息)，属性会根据一定的比例或者规则被突变和切割连接。完整的进化通常从随机生成的个体群体开始，是一个迭代过程，每个迭代中的群体称为一代。每一代都要用适应度函数(通常是目标函数)来衡量筛选更适应环境的个体；从经过选择的个体中对其基因组进行修饰(重组并且可能随机突变)，将获得的新的个体组成新的一代；在种群成熟之前，算法会不断地迭代，并可能使用不同的候选解决方案。通常情况下，经过数代进化工作，该算法终止时，基本可以得到令人满意水平的个体。

基本遗传算法的形式描述如算法1所示。

算法1遗传算法

1: 初始化一个解集，并评估每个个体的适应度

2: Repeat

3: 通过适应度函数筛选出部分个体

4: 按照“适应度越高，被选中的可能性越高”的原则，以一定的比例选择部分个体进行杂交，产生子代

5: 按照一定比例选择部分个体进行变异操作

6: until 新种群产生

2 遗传算法并行化策略

当问题的规模和复杂程度不断增加以后，遗传算法收敛到全局最优所花费的时间也更长。遗传算法具备天然的并行性，并且并行机目前也比较普及，为遗传算法的并行化奠定了基础。常见的并行化策略主要有以下几点：

(1) 适应度评价函数 个体适应度评价需要占用一定的时间，提升计算个体适应度的效率，可以通过研究并行化遗传算法的适应函数，找到并行计算个体适应度函数的恰当表达方式，可以有效地提升遗传算法的选择效率。该方法依赖于数值的开发成果和并行化研究。

(2) 产生新种群 前文已经提到遗传算法中个体的选择是同时完成的，不同个体的适应度相互独立的，彼此之间互不影响。在适应度函数评价个体的时候可以采用并行化策略，因此，计算个体适应度可以分发给不同的机器上完成。同理，简单遗传算法的交叉、变异过程都可以实现并行化。

(3) 种群分组 前面的方法主要还是根据遗传算法本身的特点进行改进。需要注意的是：可以将一个遗传算法用在多个种群上，例如可以将遗传算法放在集群环境中，同时处理多个种群。将种群分组则对简单遗传算法的结构进行改进，在并行机上实现起来相对来说也更加简单。

2.1 四种基本模型

运用分而治之的思想，文献[21]最早在大型的并行计算机上应用并行遗传算法PGAs(Parallel Ge-netic Algorithms)。同时分而治之的思想有多种实现途径，目前并行化遗传算法主要有4类模型：主从模型、孤岛模型、邻域模型、混合模型。

(1) 主从模型 主从模型易于实现，是遗传算法的直接并行化方案之一。仅有一个种群，种群的选择交叉变异等操作都在主节点机上完成，适应度的评价在从节点机完成。从节点接收主节点发送过来的个体，主节点获得从节点计算的个体适应度值。文献[22]设计了基于MPI的可重用的主从式PGAs框架；文献[23]将主从PGAs运用到模糊关联规则的挖掘算法，加速性能比提升了19.1%。

当模型需要大量的计算适应度的工作的时候就可以采用这种并行化方案，但是也存在着主节点和从节点之间通信延迟或者瓶颈问题，负荷不均匀的问题等，导致并行失效。

(2) 孤岛模型 孤岛模型又被称为分布式模型或者粗粒度模型，这种模型适合如Transputer的多处理机系统的MMD机器或者是集群环境。先依照节点机的个数分布成多个种群(或者是子群体)，子群体在自己所在的节点机上运行GA，在经历一定的进化代数(进化时间)以后，子群体交换部分个体，丰富了子群体的多样性，降低了未成熟就收敛的可能。目前孤岛模型的研究热点主要是确定迁移规模、迁移拓扑以及迁移策略问题。文献[24]将粗粒度并行遗传算法与动态规划相结合，孤岛模型的加速比提升，且通信开销较小。文献[25]将遗传规划算法与粗粒度并行遗传算法结合，并用语言数据实验证明新算法的预测误差更低。

(3) 邻域模型 邻域模型，或称细粒度模型，常用于连接机或者是多处理器系统阵列式SIMD系统的机器。该模型对于每个个体都在所在的处理机或者是邻域处理机上完成，几乎没有全局操作，充分展现了遗传算法的特性。邻域模型中的每一个处理机都只分配一个个体，将一个个体视为一个子群体，子群体只和邻接子群体交换信息。在文献[26]中提出了基于GPU的细粒度并行化遗传算法，提升了算法的运行速度。文献[27]提出了细粒度模型在Hadoop的MapReduce上并行编程求解最短路径，取得了优于经典遗传算法的效果。

邻域模型的关键是采用什么样的邻域结构，因为邻域结构极大地影响了个体在种群当中的传播路径以及个体的空间位置。目前采用什么样的邻域拓扑最优尚无权威说法。根据Shapiro B的理论，在海明距离r>2的时候，效果较差，并且通过对r内所有邻域实验后发现4邻域模型比8邻域模型效果更好。

(4) 混合模型 近几年来出现了较多的混合模型，主要是将前三种基本模型进行整合形成新的层次结构。例如混合模型中有：细粒度-粗粒度模型、粗粒度粗粒度模型以及粗粒度-主从式模型，上层模型将下层并行结构模型视为一个种群，下层模型中的子群体则是真实的子群体(种群)。一般来说下层模型中内部信息交换量比较大。文献[28]提出了一种分层遗传算法解决了作业车间调度问题。

以上的模型根据其自身的特点来说，各有优劣。主从模型适合计算时间主要在评估适应度环节的问题，使用范围有限。细粒度模型对处理机的要求比较高，目前就适用于小范围直径还是大规模邻域尚有争议。粗粒度模型的通信开销小，加速比呈线性，因此使用范围比较广，适合在通信带宽低的集群环境上运行，不过，目前对采用什么样的迁移策略和迁移规模来说仍然有待进一步的研究。混合模型因为其具有较好的并行性，是当前研究的主流模型，在混合模型当中，粗粒度-主从式模型运用效果较好[29]。

常见的实现并行化遗传算法的并行机主要有多数据流、多指令流的MIMD机器，粗粒度的并行计算机，多数据流、单指令流的SIMD机器，细粒度的并行计算机等，还可以在局域网环境或者是集群环境下实现并行算法。需要根据具体的实现方法来选用不同的硬件环境。

2.2 并行化性能评估标准

加速比是评级多核架构性能的主要参数。加速比是串行和并行时间的耗时比。例如并行耗时5.9单位，串行耗时95.1单位，那么加速比即为16.12。依据多核处理器加速比已有的研究，现在对并行化遗传算法的评价模型进行介绍。

2.2.1 固定任务模型

评价并行化遗传算法的性能的指标有很多，其中最常见的就是Amdahl定律中的加速比。

原始的加速比的原理如下：假设有p个并行机，可以组成一个性能更高的并行化运行平台。单个计算节点的运算速度(即性能)为1，p个计算节点所创建的结构的串行性能为pref(p)。已知加速比为串行运行时间与并行运行时间之比，即：

(1)

式中：T1是串行计算所需的时间；Tp是该算法在p个处理机组成的并行机上的运行时间；Sp即为加速比。

假设问题为w，单个计算节点执行任务的时间即为：

并行化运行平台的基本执行时间为：

(2)

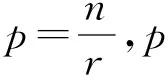
(3)

令perf(p)=c,c为常数，则有：

(4)

式(4)在c=1的时候就是大型机之父的理论解析式，系统功效提高的程度和总执行时间以及执行方式有关：

(5)

f是并行处理部分在整个系统中的占比；对应的，(1-f)就是串行处理的部分在整个系统中的占比。m是并行处理机的数量，Speedup即为加速比。固定模型的三维图解变化趋势如图1所示。

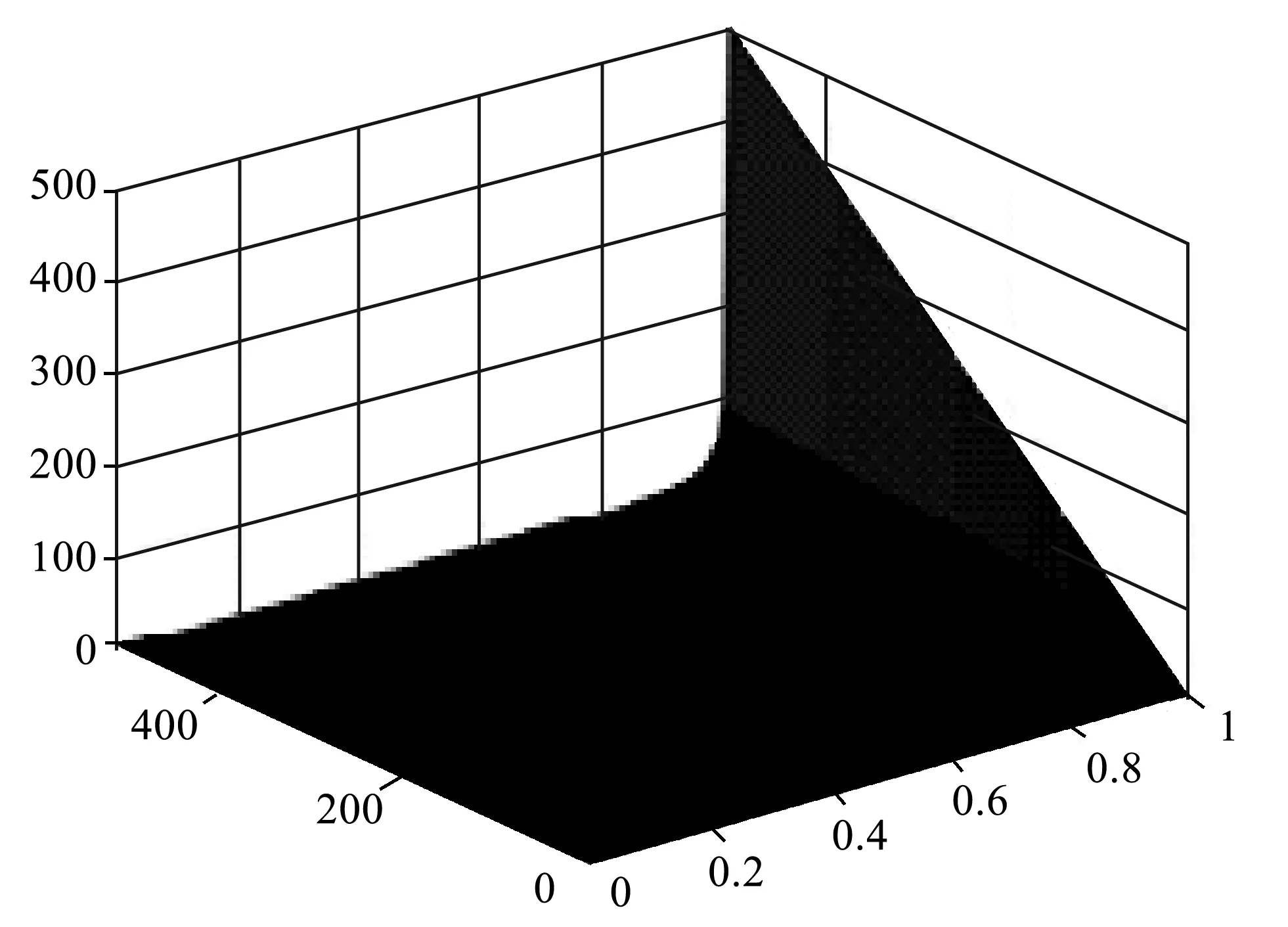
图1 固定任务模型加速比变化趋势图

该定律主要适用于负载固定的情况，例如在主从式模型中可以得到几乎呈线性的加速比；而在孤岛模型当中，当群体规模恒定，子群体的规模与数量不成正比的时候，其加速与主从式模型加速比相同。目前该定律在邻域模型中运用的较少[29]。

2.2.2 固定时间模型

文献[30]于1988年提出了Gustafson定律。

假设原始任务为w,比例扩增任务为w′，在同等的时间内，p核并行和串行完成的任务相同，则有：

w′=(1-f)w+fmw

(6)

那么：

(7)

固定时间的三维模型图解变化趋势如图2所示。

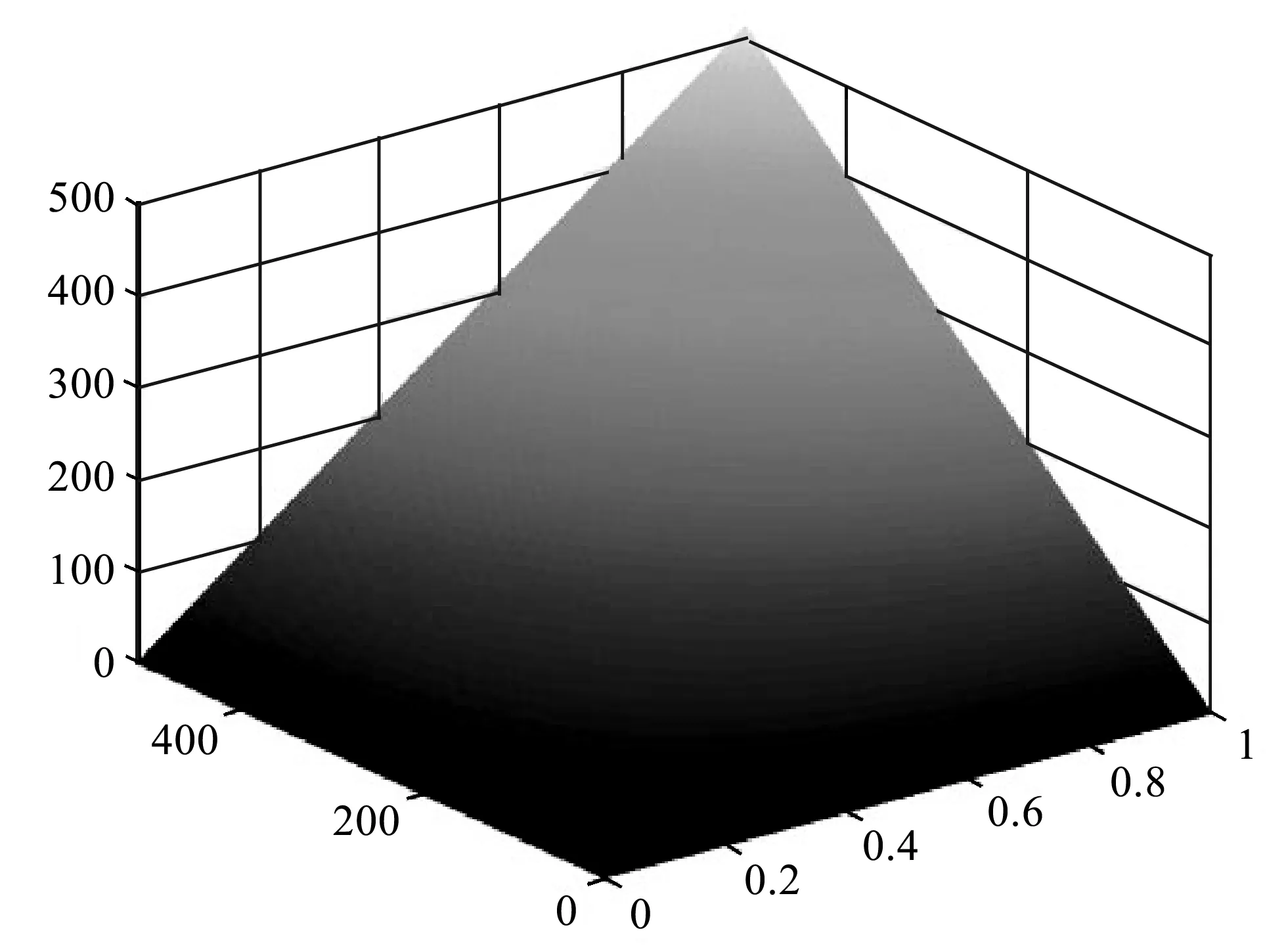
图2 固定时间模型加速比变化趋势图

2.2.3 其他模型

文献[31-32]结合实际问题给出了其他两种评价指标：(1) 改进了Amadahl定律的加速比，先确定一个适应度指标，当个体适应度高于此指标的时候，穿行计算的时间与并行计算的时间之比为加速比。(2) 计算并行运算和串行运算获得个体的最高适应度的差值大小。

另外还可以设计多个指标，例如增加平均进化代数、平均计算时间等因素，设计成具有不同集合特点的测试函数来比较不同模型之间的优劣。

3 遗传算法的研究和未来发展方向

本文重点考察了近五年国内外工程技术人员以及相关领域研究者在遗传算法方面的研究情况，数据来自2013年-2017年已发表在核心期刊上的“工业技术类”有关遗传算法的研究。图3是遗传算法在包含函数优化、生产调度、自动控制、图像处理、人工智能、遗传编程、数据挖掘、机器学习以及遗传算法综述以内10个方向的应用，图4是遗传算法在编码策略、遗传算子、物种多样性、测试函数、收敛性、欺骗问题和综述等7个方面文献的统计结构。

图3 2013年-2017年遗传算法应用领域分布柱形图

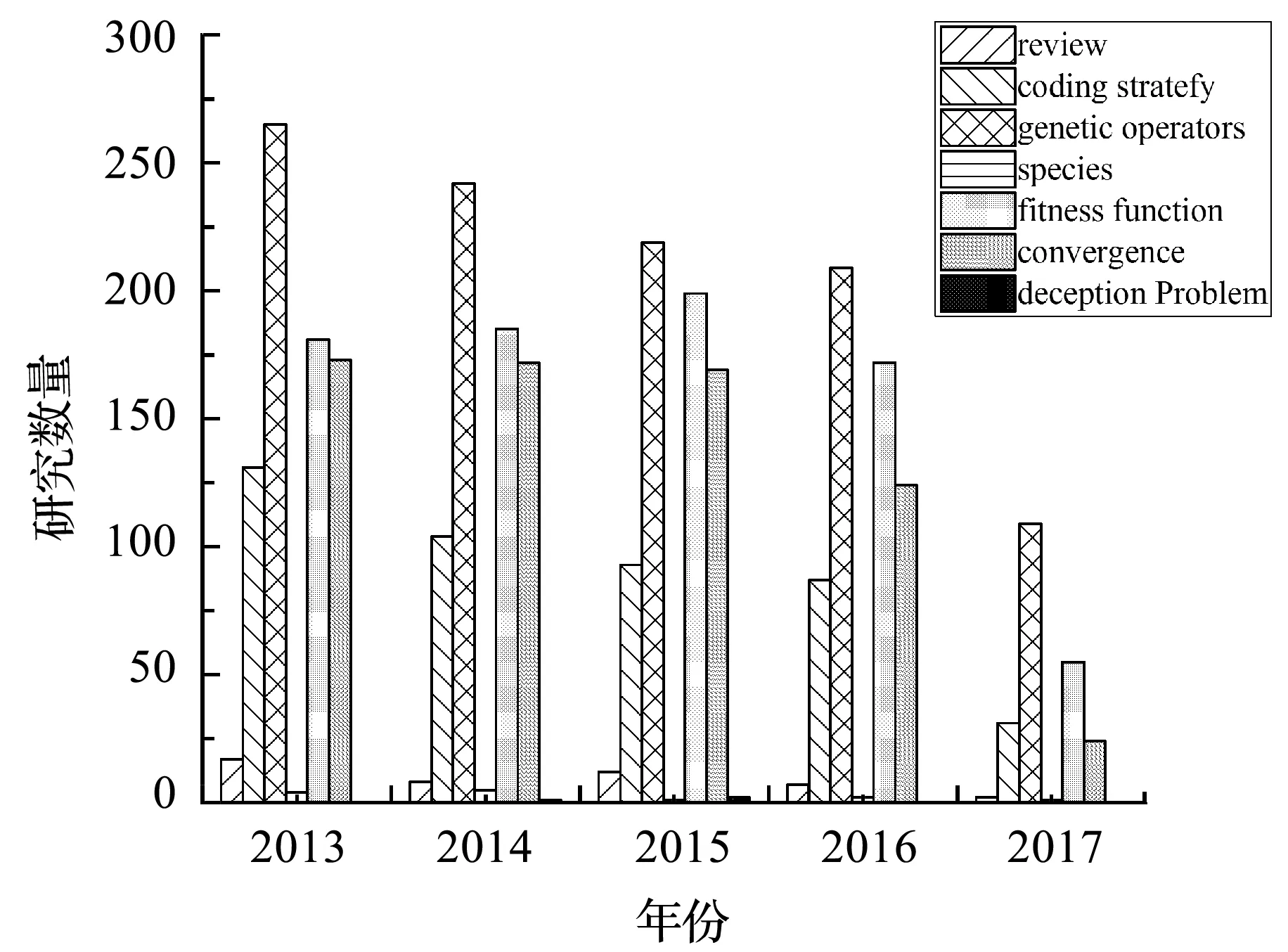
图4 2013年-2017年遗传算法研究领域分布柱形图

根据图3、图4可以得到如下结论：

就应用领域而言，遗传算法的主要应用方向集中在机器人学、数据挖掘和机器学习方面。在生产调度中的应用基本呈现出逐年增加的趋势。

就研究方向而言，遗传算法研究的热门在遗传算子、测试函数、收敛性和编码策略上。相比而言，在物种多样性和欺骗问题上研究成果不多，有待更深层次的研究。

整体而言，2016年以前遗传算法领域的研究持平，说明遗传算法仍然是机器学习领域和数据挖掘领域的研究关键点。加上真正有效的成果在总体的研究成果中占比较少，因此遗传算法仍然是一个值得进行深入研究的领域。

遗传算法具有鲁棒性强的特点，即可以用一个通用的框架来系统的解决优化问题，目前已经取得了较多的成果。在研究应用方向层面，函数优化是评价遗传算法的基本算例，多样化的测试函数有助于体现算法的性能和效果。文献[33]提出了一些多极值并具有最优点的函数。对于如背包问题、布局优化、旅行商问题、图形划分等NP-hard问题，解空间急剧上升，已经不能用枚举法或是暴力求解法解决问题。文献[34-36]成功地将遗传算法运用到求解TSP问题上，文献[37-39]分别将遗传算法运用到了排课问题、车间作业调度问题上。在自动控制方面，文献[40]用遗传算法优化了航空控制系统，文献[41]利用遗传算法对模糊控制器进行了优化。在机器人方面，遗传算法也被广泛的运用，例如文献[42]将遗传算法运用到机器人移动的路径规划。图像处理对降低图像分割、扫描等操作的误差有一定的要求，因此可以用遗传算法进行优化计算。文献[43-45]分别将遗传算法运用到汉字识别、图像恢复和图像边缘特征提取上。在机器学习领域，遗传算法可以通过学习模糊控制规则来改进模糊系统的功能，文献[46-47]已经将遗传算法用来调整CNN的连接权，以达到优化CNN结构的效果。另外数据挖掘问题也可以转换成最优解的搜索问题，数据库就是搜索空间，遗传算法随机产生一组规则，当不断进化的规则可以全面覆盖数据库的时候则进化完成[46]。文献[48]中已经开发出相应的数据挖掘工具，主要是基于遗传算法的思想，对失事飞机的数据进行数据挖掘，结果证明这种方法十分有效。

在研究领域，编码方式是遗传算法的关键之一，遗传算法之父Holland建议用二进制。文献[49]提出了多目的进程调度二进制编码方式，强调识别关键产品、单位、任务，仅将少部分变量进行二进制编码。文献[50]提出混沌gary编码方式，对于多参数的优化问题来说实数编码的效果更好。文献[51]针对实数编码仅适用于连续变量问题，提出了将混沌变异与映射到量子位的实数染色体交叉的编码方式。文献[52]为了减低早熟的概率，将复数的思想运用到遗传算法的编码方式中。文献[53]提出了基于动态相似度的零件族编码，优化了遗传算法的收敛时间和编码长度。

遗传算法的关键主要在于交叉、选择、变异算子的设计。文献[54]提出了局部搜索能力纳入选择算子，提升了算法在不可能解的领域找到可行解的几率。文献[55]设计了一种局部竞争选择算子，为避免陷于局部最优的问题，通过强调个体差异保证了种群的多样性。文献[56]将模拟退火算法运用到选择算子中，提升了算法的稳定性。文献[57]提出了拉普拉斯交叉算子，达到实现遗传算法稳定高效的搜索的效果。文献[58]通过高斯分布概率调整了实数编码的交叉算子。文献[59]提出了单亲遗传算子，确保最终一定找到可行解。文献[60]提出了功率变异算子。文献[61]设计了定向编译算子，提升了交互遗传算法的性能。文献[62]提出了贪婪子循环算子，提升了遗传算法在TSP问题中的性能。

遗传算法中涉及到位串、交叉概率、变异概率和群体规模等参数的设计。文献[63]设计了一套模糊规则，在线动态地改变交叉概率和变异概率。文献[64]则用条件发生器来产生交叉和变异概率，具备一定的稳定倾向性和随机性。文献[65]通过大量实验提出了针对调度问题的最佳遗传算法参数。文献[66]针对遗传算法存在的早熟问题，提出了遗传优势原则，让交叉概率和编译概率自适应的改变。

收敛性是优化问题的重要考核指标，目前主要是运用Markov链来证明遗传算法的全局收敛性。文献[67]阐明了遗传算法收敛性的定义，并提出了新算法解决多峰值优化过早收敛问题。文献[68]运用齐次Markov链证明了当保留了上一代最优个体的经典遗传算法可以收敛到全局最优。文献[69]阐明了遗传算法出现早熟问题的原因，提出了新的遗传算法收敛理论。

建筑块理论认为在遗传过程中低阶短距、适应度高的模式将会以指数级别增长，并转变成高阶长距、适应值高的模式。但受到“欺骗条件”的影响，最终可能会形成非最优模式，导致问题最终无法收敛到全局最优解，这就是欺骗问题。文献[70]给出了模式欺骗和遗传算法欺骗问题的定义，并讨论了欺骗问题和收敛性和并行性的问题。文献[67]提出了解决连续性欺骗问题的定向变异算子。文献[71]计算了部分领域的遗传算法解决完全欺骗问题的所需的平均值时间。

4 结 语

遗传算法为解决复杂优化问题提供了通用模板，是近些年进化算法研究的热点之一。同时统计数据还表明遗传算法已经渐渐走向了应用，目前已经较为广泛地运用在数据挖掘的技术中，改进也是当前遗传算法的研究热点。纵观遗传算法的研究方向可以发现，主要仍集中于机器学习和数据挖掘等方面，并呈现出逐年增加的趋势，但是在机器学习领域实际应用成果方面并不丰富。因此还存在进一步的发展空间，在欺骗问题等理论问题研究方面尚有欠缺。整体来看遗传算法还有相当的发展空间，未来发展主要集中在以下几个方面：

1) 遗传算法未来会在并行化方面进一步发展。目前数据挖掘的运用较多，并行化遗传算法能够显著地提升运算速度，有较高的应用价值。

2) 遗传算法目前在欺骗问题、参数设定等理论性研究方面尚显不足。这限制了遗传算法更深层次的发展，因此未来遗传算法的研究重点可能会更多的出现在理论方面，建立起相应的数学基础。

3) 遗传算法会与其他技术进一步融合。因为遗传算法的局部搜索能力较弱，存在着早熟收敛的风险，需要和其他能够快速局部收敛算法相结合才能实现更有效的收敛策略，这需要大量的实验和理论研究来实现。

4) 算法的早熟机理、参数设置的理论指导、收敛速度等理论研究可能会成为后进的研究热点。这些理论将指导算法发展的方向，目前还有很多不足，因此仍然有发展的空间。

5) 并行化理论研究方面未来会更加深入。遗传算子之间相互独立，个体与个体之间的适应度选择过程也都相互独立，具备并行化的天然优势。设计对应的并行策略和并行遗传算子，建立相应的数学基础，尤其是在数据挖掘领域，显得十分必要。