基于雷诺数和直径比两个因素的同心环状缝隙流轴向速度试验研究

孙 蕾

(1.临汾市水利勘测设计院，山西 临汾 041000；2.太原理工大学水利科学与工程学院，太原 030024)

0 引 言

在液压技术问题的分析，研究和工程计算中，经常要用到流体力学中的同心环状缝隙流理论[1]。缝隙流动对液压传动的影响非常显著，液压泵、液动机、换向阀等液压元件中处处存在着缝隙流动问题，缝隙流动的流量有时就是液体机械中的液体泄漏量，缝隙过小增大了摩擦，缝隙过大又增加了泄漏[2]，过大的泄漏量不但造成能量损失，而且影响执行机构的正常工作[3]，比如换向阀的阀体和阀芯之间的缝隙就是规则的环形缝隙，要研究和改善机械性能，必须了解缝隙流动的特性[4]。同心环状空间是工程中较为常见的流体流动空间，在此空间中流体流动情况比较复杂[5],目前对同心环状缝隙流的研究主要是针对微小间隙中油的流动，而以水为载体的缝隙流的研究相对很少，赖邦钧等[6]人对环形缝隙的泄漏水量进行过测定并推导出计算公式, 但并没有对其流动特性进行研究分析。本文主要针对这一问题展开研究。

水液压技术目前已成为当今世界液压技术领域的前沿研究课题之一[7]。当压力水作为传动介质时，工程流体力学中的环形缝隙流的层流规律[8]不再完全适用，在工程实际应用中，环形缝隙中的水流流动一般为紊流流动[9]，紊流中由于液体质点的相互混掺，互相碰撞，产生了液体内部各质点的动量传递，动量大的质点将动量传给动量小的质点，动量小的质点影响动量大的质点，造成流速分布的均匀化[10]，所以选择缝隙流的轴向平均流速进行研究。

1 缝隙流轴向速度的公式推导

连续方程是质量守恒定律在运动流体中的数学表达式，为了简化数学模型，建立如图1所示的圆柱体在平直管段内平稳运行的简易模型，可以认为圆柱体以恒定速度Vc运动，则Δt时段内流入管段的液体的总质量mb应等于由于圆柱体运动而流入管段中液体的质量ma和缝隙内流入液体的质量mc之和，即：

mb=ma+mc

(1)

(2)

(3)

(4)

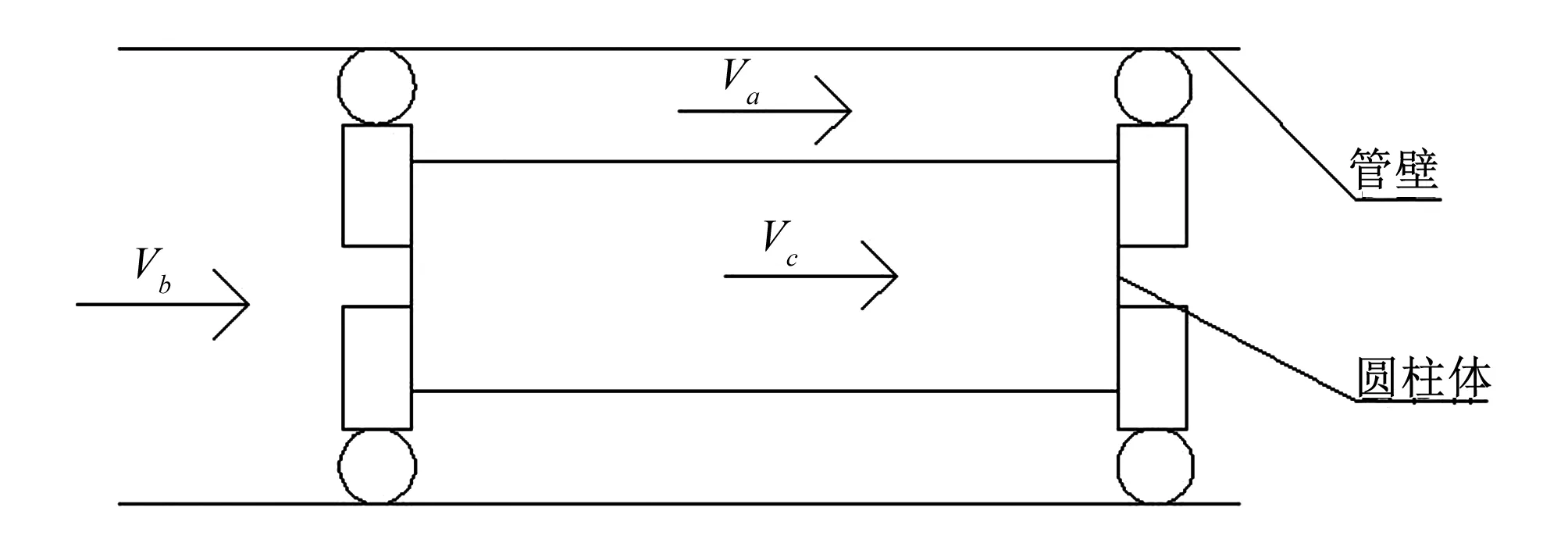
图1 圆柱体在平直管段平稳运行图

将式(2)、(3)、(4)代入式(1)，得：

(5)

式中：ρ为水的密度；D为管道内径；d为圆柱体外径；Va为环状缝隙水流轴向平均流速；Vb为管道水流平均流速；Vc为圆柱体运行速度。

直径比是指圆柱体的外径与管道内径的比值，记为k=d/D，代入(5)式得：

(6)

由式(6)可以看出缝隙内水流的轴向速度Va是由受管道水流速度Vb、圆柱体的运行速度Vc和直径比k共同决定的，而管道水流速度和圆柱体的速度都是由输水流量决定的，由雷诺数的计算公式：

(7)

可知，雷诺数与流量成正比关系，所以，缝隙流的轴向速度同时受雷诺数和直径比的共同影响。

2 圆柱体运动速度研究

由式(7)可以计算出管道水流的流速Vb的值，即：

(8)

式中：v为水的运动黏度。但圆柱体的运动速度不能计算出来，需通过试验进行测得。试验系统[11,12]由4部分组成：动力与调节装置、投放与接收装置、试验管道系统和测试系统。测试系统[13]主要包括时间、流量测试装置和数据采集装置，测试流程图如图2。

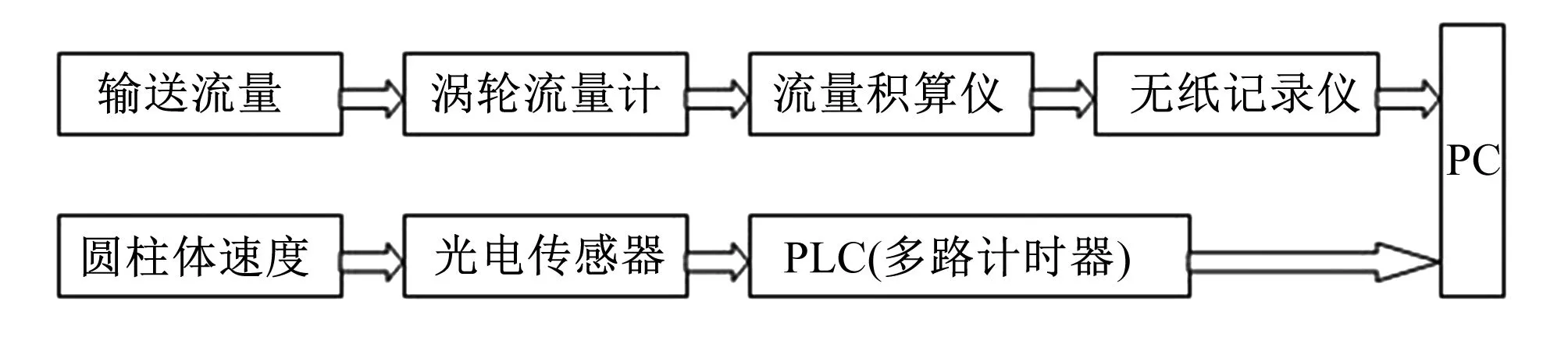
图2 测试流程图

为了研究雷诺数和直径比对环状缝隙流轴向速度的影响，试验选择5个雷诺数Re：155 350、140 467、175 584、210 700、245 817，4个直径比k：0.5、0.6、0.7、0.8，分别测得不同工况下的速度，根据需要在管路上安装了光电感应器并连接至PC机。光电感应器由一台激光器和一支光电管组成，固定在管道上。激光器发出的光透过有机玻璃管进入光电管时,会有连续的电压产生,当激光束被经过的圆柱体挡住时,光电管接收不到信号,连续电压就会中断,通过PC机记录两台感应器电压中断的时间间隔,并根据两台感应器的距离即可算出圆柱体在管路中运行的平均速度。如表1(表中数据均为无量纲数，定义所有数据中的最大值为参考值，各个速度与最大值的比值为该工况下的速度值，图3和图4中数据处理方式同理)。

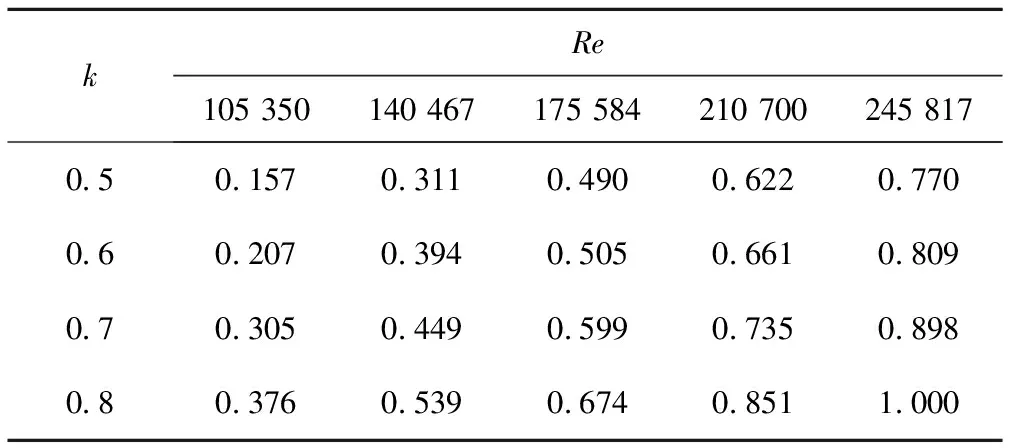
表1 不同雷诺数、不同直径比下圆柱体的平均运动速度 m/s

由表1可以看出，雷诺数越大，圆柱体的运动速度越大；直径比越大，圆柱体的运动速度也越大。圆柱体在平直管道中的运动是由圆柱体前后端面的压力差以及柱身受到的剪切力引起的，当圆柱体的长度和质量一定时，Re越大，圆柱体的运动速度越大[14]，当Re，圆柱体质量和长度等因素都一定的前提下，直径比越大，圆柱体两端面的面积增加，受到的压力差增大，同时柱身的侧面积也增加，剪切力的受力面积增大，总之圆柱体受到的总动力是增大的，所以其平均运动速度随着直径比的增大呈现上升的趋势。

3 缝隙流轴向速度研究

3.1 雷诺数对缝隙流轴向速度的影响

雷诺数是反映流体力学中惯性力对黏滞力的比值，雷诺数越大，意味着惯性力的影响越显著。由图3可以看出，环状缝隙流的轴向速度随雷诺数的增大而增大，经线性拟合后，其R2均高于0.99， 基本成正比的线性关系。这主要是由于流量为缝隙流的轴向运动提供动力来源，其主要体现在压差力，压差力随流量的增大而增大，即流量越大，作用于缝隙流上的主要动力就越大，而雷诺数又与流量成正比关系，所以雷诺数越大，缝隙流的轴向速度也越大。

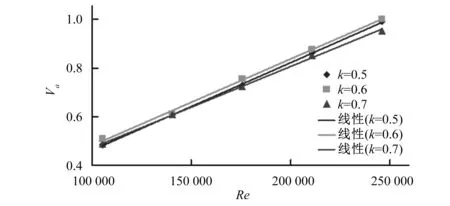
图3 缝隙流轴向速度随雷诺数的变化曲线

图4 缝隙流轴向速度随直径比的变化曲线

3.2 直径比对缝隙流轴向速度的影响

(8)

不能确定式(8)大于零还是小于零，所以Va随着直径比的变化不是单一趋势。

由式(5)得，流入管段液体的总流量应等于由于圆柱体运动而流入管段中液体的流量和缝隙内流入液体的流量之和，即：

Q=Q1+Q2

(9)

Q1随着圆柱体速度的增大而增大，圆柱体的速度又随着直径比的增大而增大，所以直径比越小，Q1越小，由式(9)则Q2越大，但直径比越小缝隙水流的过水断面面积越大，k<0.5时,过水断面面积的增大速度大于缝隙流量的增大速度，所以缝隙流的速度是减小的；直径比越大，Q1越大，由式(9)则Q2越小，但直径比越大缝隙水流的过水断面面积越小，k>0.7时，过水断面面积的减小速度小于缝隙流量的减小速度，所以缝隙流的速度也是减小的。由图4可见，直径比范围在0.5～0.7时，环状缝隙流的轴向速度最大。

3.3 缝隙流流速、管道水流流速、圆柱体速度三者之间的关系

两相流中的一个重要特征是存在着一相通过另一相的“滑移”，即密度与黏度均不同的两相流动，其中一相倾向于比另一相以更高的速度流动。环状缝隙流与圆柱体之间存在着剪切力的作用，以应力形式表示，记为τc，其大小和方向取决于圆柱体的运动速度Vc与环状缝隙流的轴向速度Va的大小关系。

为了定性的分析缝隙流流速、管道水流流速、圆柱体运动速度三者之间的关系，对Va、Vb、Vc的值进行处理，定义V1=Va/Vb,V2=Vc/Vb,V3=Vb/Vb=1,则可以得到V1、V2、V3随雷诺数和直径比的变化趋势。图5为k=0.5、0.6、0.7时，V1、V2、V3随雷诺数的变化曲线，图6为Re=210 700和24 5817时，V1、V2、V3随直径比的变化曲线。

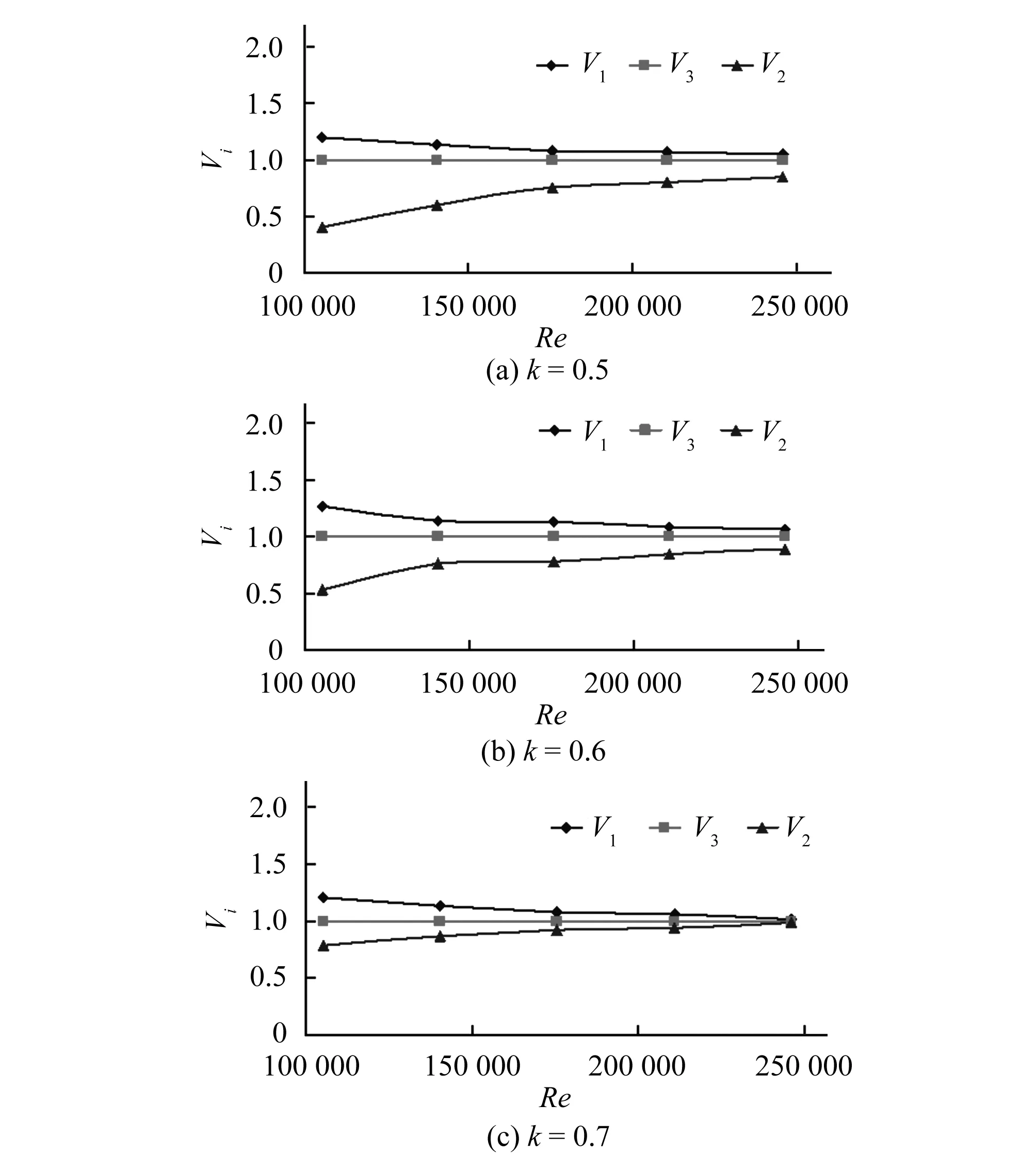
图5 不同雷诺数下V1、V2、V3之间的关系

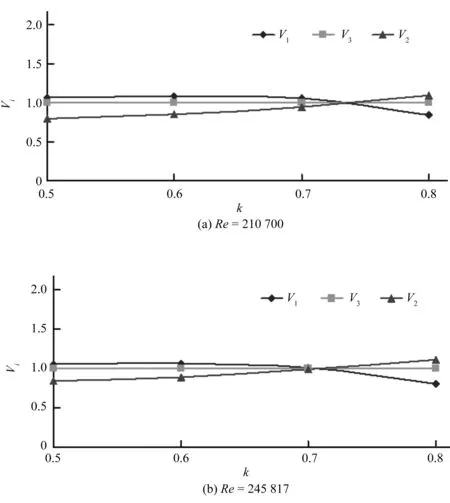
图6 不同直径比下V1、V2、V3之间的关系

在同一雷诺数下，管道水流的速度Vb是不变的，所以图6中V1和V2的变化趋势反映的就是Vc和Va的变化。由图7可以看出随着直径比的增大，V1和V2向V3靠拢，三者在某个直径比时相交于一点，而后又成分散趋势，在交点处圆柱体的运行最平稳，管道水流和环状缝隙流也达到稳定状态，相交之前，缝隙流速最大，圆柱体速度最小，相交之后相反。因此，当管道水流的雷诺数确定时，存在一个最优直径比ke使系统的运行最平稳，而且随着雷诺数的增大，达到稳定运动状态所需要的直径比越来越小。

从缝隙流量和系统稳定运行这两个角度综合考虑雷诺数和直径比对缝隙流轴向速度的影响时，建议选择雷诺数的范围为210 700～245 817，直径比为0.7。

4 结 语

为了研究雷诺数和直径比对环状缝隙流轴向速度的影响，以及环状缝隙流速、管道水流速度和圆柱体的速度三者之间的关系，得出了如下结论。

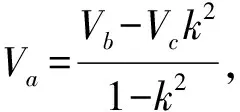
(2)环状缝隙流的轴向速度随雷诺数的增大而增大，基本成正比的线性关系；在同一直径比条件下，雷诺数越大，圆柱体速度增大的最快，管道水流速度次之，环状缝隙流速增大最慢，且三者在最优雷诺数Ree时相交，相交之前环状缝隙流速最大，相交之后圆柱体速度最大。

(3)环状缝隙流的轴向速度随直径比的变化不是单一趋势，而是先增大后减小，直径比范围在0.5～0.7时，缝隙流的速度最大；在同一雷诺数下，环状缝隙流速、管道水流速度、圆柱体速度相交于最优直径比ke，相交之前，环状缝隙流速最大，相交之后相反。

(4)随着雷诺数的增大，达到稳定运动状态所需要的直径比越小；随着直径比的增大，达到稳定运动状态需要的雷诺数越小。因此从缝隙流量和系统稳定运行两个角度综合考虑雷诺数和直径比对缝隙流轴向速度的影响时，建议选择雷诺数的范围为210 700～245 817，直径比为0.7。

□