基于雨型的小流域雨量预警指标不确定性研究
原文林,刘美琪,宋汉振
(郑州大学水利与环境学院,郑州 450001)
我国山洪灾害呈现多发、易发、频发、重发的特点,1949年以来因山丘区爆发的山洪灾害所造成的人员伤亡占洪涝灾害死亡人数的70%以上[1]。山洪灾害已成为威胁人民群众生命财产安全的突出隐患,是我国防洪减灾工作中亟待解决的突出问题[2]。目前国内预报山洪灾害发生与否,采用最多的方法是利用雨量预警指标来判别。因此,提高雨量预警指标精度对于准确发布预警信息,减少人员伤亡和财产损失具有非常关键的作用。
雨量预警指标(临界雨量)计算方法众多,对山丘区小流域常采用水位流量反推法[3],而设计洪峰值是确定雨量预警指标的一个重要参数。由于山区较缺乏降雨径流资料,水文模型参数无法直接率定[4],难以精确计算洪峰值。为此,借助地区暴雨图集(水文手册),通过设计暴雨推求设计洪水的方法在实际工程实践中被广泛应用[5]。在设计暴雨洪水计算时,涉及降雨量在时程上的分配问题,即雨型的确定。岑国平[6]在1998年研究表明,设计暴雨雨型对城市、机场排水设计中的洪峰流量具有一定影响。Jain等[7]计算无资料地区洪水时发现,设计洪峰对设计暴雨模式及时间分配比较为敏感。范泽华[8]利用Huff雨型推导了天津市设计雨型,并提出时段雨型,得到了更为精细的降雨时程分布。Mca P等[9]通过模拟不同降雨时程分布过程所形成的洪水,发现降雨时程分布对洪水汇流具有影响。林木生等[10]通过建立洪量与暴雨特征因子的关系,分析暴雨时空变化对洪水要素的影响,发现暴雨时间变差系数对洪峰流量具有显著影响。侯精明等[11]通过对城市不同雨型的内涝或暴雨积水量进行模拟,揭示了暴雨雨型对城市内涝积水程度的量化规律。
上述研究体现了雨型在城市暴雨洪水研究中具有一定的作用。但是山洪灾害预警研究时,雨型的基础作用还未过多体现。设计暴雨洪水计算中若忽略了雨型的基础作用,当实际降雨过程与采用的设计雨型吻合度较低时,可能导致设计洪水成果与实际情况相差较大,雨量预警指标就会存在偏差。因此,解决上述问题的关键就在于考虑小流域雨型的准确性和适用性。本文以裴河小流域夏湾组作为预警对象,采用模糊识别法分析最可能出现的暴雨雨型,在裴河小流域降雨特性分析基础上,结合地区暴雨图集中的设计雨型,分析不同雨型对临界雨量的影响,并揭示雨型与临界雨量间的响应关系,研究成果对于提高山洪灾害雨量预警指标精度具有重要的理论研究和实际应用价值。
1 雨量预警指标计算方法及原理
目前常用的雨量预警指标计算方法主要包括数据驱动法、水文水力学法两类。其中,数据驱动法应用时缺乏一定的物理理论基础,使统计归纳计算的雨量预警指标存在数据系列非一致性的问题。因此,随着对山洪灾害雨量预警指标的进一步认识,根据流域特征、河道断面成灾流量(水位)等信息,通过产汇流计算并反推相应降雨量的水文水力学法也逐渐成为计算雨量预警指标的常用方法,即水位流量反推法。雨量预警指标计算过程中主要涉及设计洪水计算、临界雨量计算两大部分。
1.1 设计洪水计算方法
设计洪水计算包括产流计算、汇流计算。产流计算方法常用径流系数法[12]、降雨径流相关图法[13]、初损后损法[14];汇流计算方法常用经验公式法、推理公式法、单位线法等[15]。根据山丘区小流域特征,在满足精度要求并计算方便适用的条件下,产流计算多采用降雨径流相关图法。本文依据《河南省中小流域设计暴雨洪水图集》中“河南省山区丘陵地区降雨径流关系曲线图”计算净雨过程。
由于汇流计算中需要用到暴雨时程分配过程,即雨型,为此选用瞬时单位线法计算洪峰流量。Nash瞬时单位线法基于串联线性水库假设的水文汇流经验模型,该模型应用的关键是确定n、K两个汇流参数。其中,n是综合反映流域调蓄能力的参数,K是反映流域汇流时间的参数。瞬时单位线数学公式表达式为:
(1)
式中:u(0,t)为瞬时单位线纵高;Г(n)为伽玛函数。
瞬时单位线是由瞬时净雨产生的,汇流计算时需通过S(t)曲线将其转换成时段单位线,S(t)曲线为瞬时单位线方程的积分,即:
(2)
时段单元过程线为:
u(Δt,t)=S(t)-S(t-Δt)
(3)
从而推求由瞬时单位线转换的时段单位线公式:
(4)
则汇流出口断面流量过程为:
(5)
根据以上原理,瞬时单位线法计算步骤可概括为:①推求设计暴雨时程分配过程;②利用产流计算方法,计算各时段的净雨深,并之和等于总的径流深;③确定n、K两个汇流参数;④根据n、K值,由瞬时单位线推求时段单位线;⑤各时段净雨量乘以时段单位线,经过叠加后生成小流域的洪水出流过程。
1.2 临界雨量计算方法
本文临界雨量计算采用广泛使用的水位流量反推法,其假定小流域控制断面处有一洪峰流量Qm,存在某个预警时段的降雨量Ht,经产汇流计算后所形成的洪水中洪峰流量等于控制断面处的洪峰流量Qm,并且该降雨量Ht的设计频率等于Qm的设计频率。
水位流量反推法基本思路:首先,由设计暴雨经过产流计算其设计净雨过程,通过汇流计算推求各典型频率下的设计洪峰流量,并点绘设计洪峰与对应频率的关系曲线Qm,p~P;然后,依据成灾流量Q灾,在Qm,p~P关系曲线上确定对应的频率P,基于临界雨量与成灾流量同频率的假定,计算频率P对应的各时段设计暴雨,即为各预警时段的临界雨量。该方法具体计算过程如图1所示。
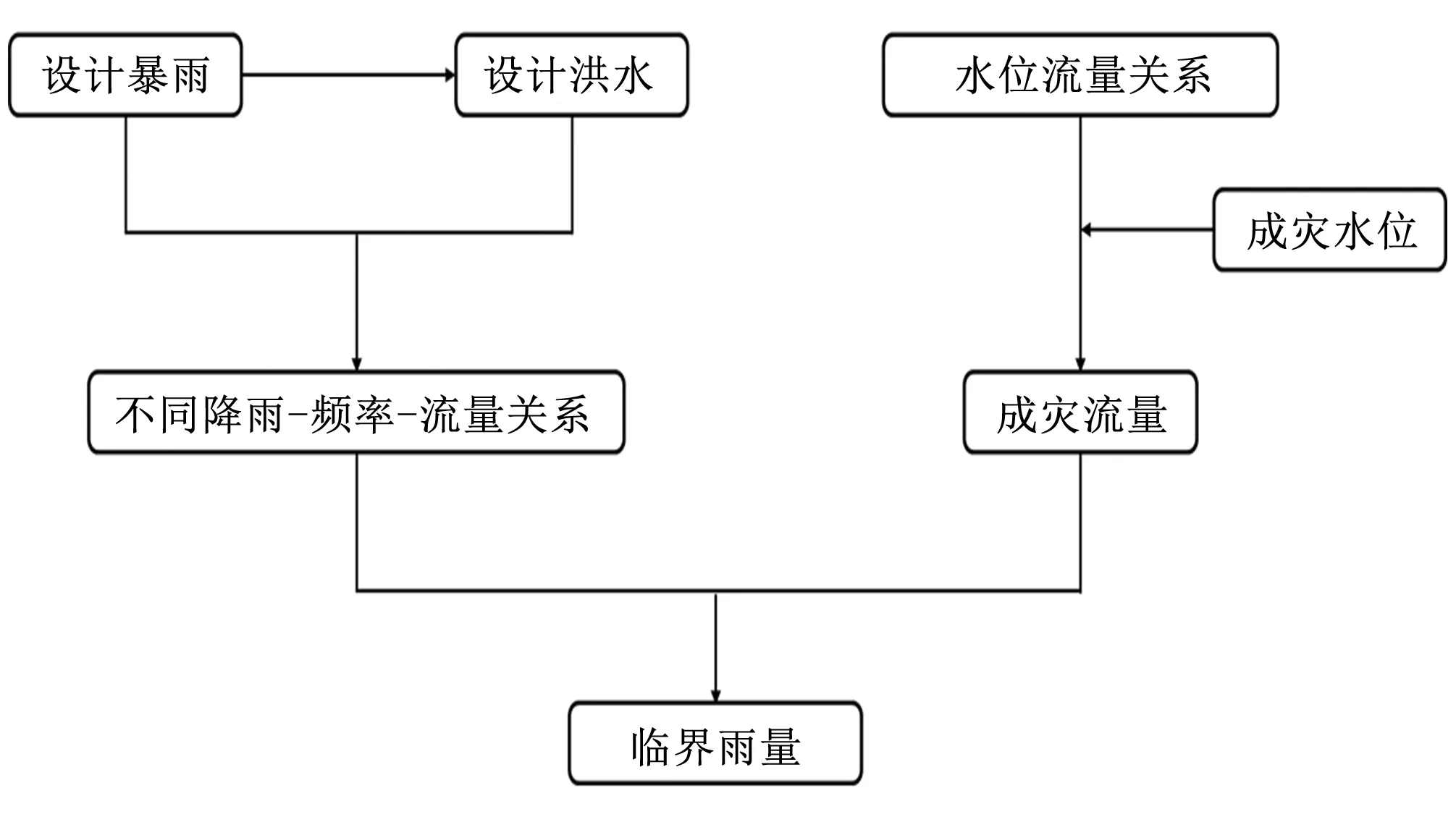
图1 水位流量反推法计算流程Fig.1 Calculation process of inversion method of water level/flow
2 裴河小流域
2.1 研究区概况
裴河位于河南省信阳市新县,属淮河流域潢河水系,控制流域面积为177 km2。研究区出口断面处有一座裴河水文站,流域内分布着董店、泗店、余河、西畈、余畈、唐畈6个雨量站。本文收集与整理了研究区内各雨量站及水文站1982-2013年降雨、径流资料。研究区位置及水文站、雨量站、水系情况示意图如图2所示。
裴河小流域所处山地,沟大谷深,呈V字型分布,坡度大多在30°以上。地表植被较少,覆盖率较低,抗御自然灾害、水土流失的能力较弱。流域内年降雨量充沛,夏季短历时强降雨较为集中。根据新县近50年的山洪灾害统计资料表明,每次山洪灾害的发生,都是在降雨量较大、雨强高的前提条件下形成的,并造成严重损失。
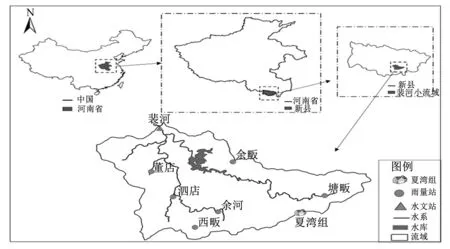
图2 研究区位置及水系示意图Fig.2 The schematic diagram of location and water system about study area
2.2 研究区降雨特性分析
统计研究区内多个雨量站32 a长系列降雨资料,采用年最大法选取各站典型降雨过程,并利用泰森多边形法计算面雨量,总共得到28场完整的面雨量过程,28场面雨量过程包含了不同雨峰位置的降雨过程,具有一定代表性。基于统计结果对研究区降雨历时、降雨类型及雨峰所处位置进行定性分析。
(1)降雨历时分析。按照雨场分割原则[16],研究区降雨历时统计结果如表1。可知研究区多以1~6 h的短历时降雨为主,占比多达64%。

表1 降雨历时统计结果Tab.1 The statistical results of the rainfall duration
(2)降雨类型分析。模式雨型将降雨类型划分为7种(如图3),采用模糊识别法[17]将28场雨量过程与模式雨型进行相似度识别,对研究区最可能出现的降雨类型进行定性分析。

图3 模式雨型示意图Fig.3 The model rainfall pattern
实际降雨过程与七类模式雨型之间的贴合度计算公式如下:
(6)
式中:k表示七种模式雨型序号;Vki表示第k类雨型第i时段的时段雨量占总雨量比例;xi表示某场实际降雨过程第i时段雨量占总雨量比例。
7种模式雨型各时段雨量占总雨量比例如表2所列。在模糊识别各降雨类型时,各场次降雨的贴合度均达到80%及以上,结果如表3所列。

表2 模式雨型各时段雨量所占总雨量比例Tab.2 The proportion of total rainfall in each period of model rainfall pattern
注:表中模式雨型各时段雨量占总雨量比例单位为%。
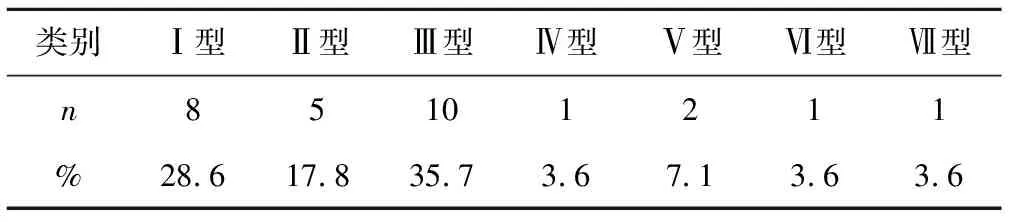
表3 降雨类型统计结果Tab.3 The statistical results of the rainfall types
表3说明研究区单峰型降雨最多,占比达82.1%,其中第Ⅰ类、第Ⅲ类降雨类型出现的可能性最大,即单峰型且雨峰偏前或雨峰居中,28场中占比分别达到28.6%、35.7%。所以本文对研究区暴雨雨型的相关分析将以单峰型降雨为主。
通过表1、表3综合分析表明,裴河小流域降雨特征可定性描述为:以短历时单峰型降雨为主,降雨量集中且雨峰偏前或居中。《河南省中小流域设计暴雨洪水图集》中6 h设计雨型的雨峰位置靠后,与裴河小流域降雨特性结果有所偏差。山洪灾害分析研究中采用唯一的设计雨型时,由于降雨的不确定性和随机性,可能导致设计洪水结果不准确,影响雨量预警指标的准确度,因此有必要探究不同暴雨雨型对雨量预警指标的影响程度。
3 实例分析
3.1 设计洪水结果分析
山洪灾害预警指标的预警时段多以1、3、6 h为主,夏湾组汇流时间为2 h。综合分析,为了预警对象的临界雨量计算准确,本文的设计暴雨洪水历时均选取6 h。
3.1.1 设计暴雨计算
由《河南省中小流域设计暴雨洪水图集》中设计暴雨公式计算夏湾组典型频率下6 h设计暴雨,其中最大1 h点雨量均值为45 mm,变差系数Cv=0.40,偏态系数Cs=3.5Cv。基于模糊识别结果中第Ⅰ类雨型、第Ⅲ类雨型及设计雨型,分别得到6 h设计暴雨时程分配过程,如图4所示。

图4 研究区三种不同的设计暴雨时程分配过程Fig.4 Time allocation process of three different design rainstorms in the study area
3.1.2 设计洪峰计算
基于上述三种不同暴雨时程分配,利用降雨径流相关法计算其设计净雨过程。因研究区土壤质地多以黏性土或壤土为主,土壤保水能力较强,所以夏季多雨期时的前期土壤含水量(Pa)为湿润状态,取土壤最大蓄水量(Wm)的0.8倍,即Pa=0.8Wm=48 mm。
设计暴雨洪水计算中采用瞬时单位线模型(IUH)计算洪峰流量。IUH涉及的参数有线性水库个数n和调蓄系数K。本文采用基于矩法估计的方向加速法确定参数n、K,其基本思路是利用矩法计算方便快捷的特点,将矩法的结果作为初始值,以拟合精度为判别准则通过方向加速法[18,19]进行参数最优化选取,即满足拟合精度时的参数值为模型最优值。
(1)参数n、K计算。本文以裴河小流域长系列径流资料,选取“峰高、量大、主峰偏后”的典型洪水20场,由矩法估算的参数n、K作为初始解,通过计算模拟多场次洪水过程,达到理论计算流量值与实测流量值尽可能吻合的目的,即拟合精度G达到收敛条件。
(7)
G(m)-G(m-1)≤ε
(8)

计算模拟了17场典型洪水过程,优选确定n=0.39,K=8.80。
(2)参数n、K验证。选取裴河其他2场典型洪水进行参数的合理性检验,其雨洪编号分别为20040718、20130526,洪峰值及洪峰出现时间差对比结果如表4所列,模拟洪水过程和实测洪水过程对比如图5所示。由表4看出洪水过程的模拟洪峰值与实测洪峰值拟合较好。图5表明模拟的洪水过程与实测洪水过程基本相同,涨洪、退水趋势也很接近,各时段模拟流量值与实测流量值吻合程度较高。
据《水文情报预报规范(GB/T 22482-2008)》可知,降雨径流预报以实测洪峰流量的20%作为许可误差,验证结果中模拟洪峰值与实测洪峰值的最大相对误差仅为7%,说明本文瞬时单位线模型的参数值是合理的,并且模型可以满足计算精度要求。临界雨量的确定是基于洪峰流量和涨洪过程,因此可利用已建立的瞬时单位线模型计算洪峰,进一步确定预警对象的临界雨量信息。
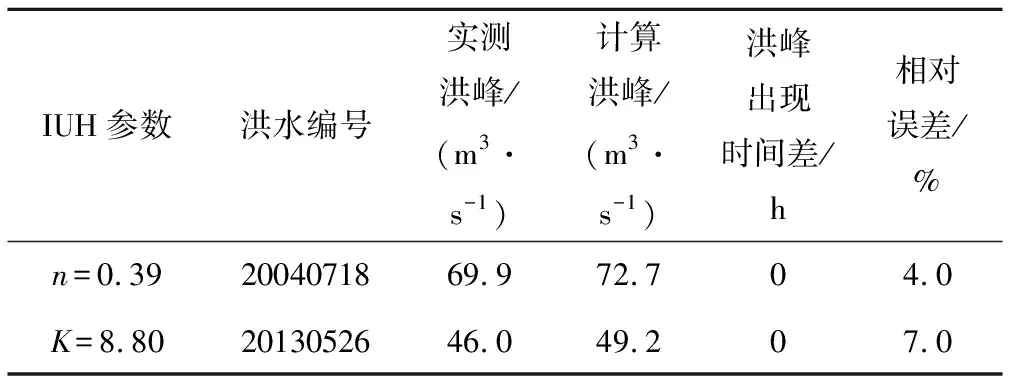
表4 瞬时单位线参数的验证结果Tab.4 Verifying results of IUH parameters

图5 洪水过程模拟值与实测值比较Fig.5 Comparison of calculated and measured data of flood process
基于上述验证合理的瞬时单位线模型,计算夏湾组各典型频率的设计洪峰流量,6 h设计洪峰结果如表5所列。
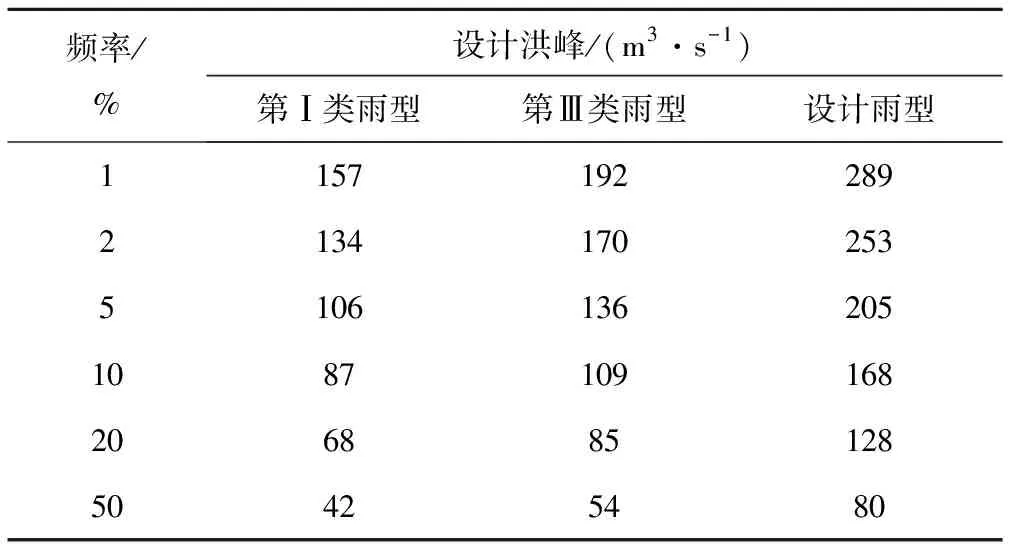
表5 夏湾组不同雨型的设计洪峰流量计算结果Tab.5 Calculation result of design flood peak flow of different rainfall patterns of XiaWan
表5结果表明,不同雨型计算的设计洪峰流量值存在偏差。同一设计频率时,设计雨型计算的洪峰值远大于第Ⅰ类雨型、第Ⅲ类雨型的洪峰值,其中第Ⅲ类雨型的洪峰值大于第Ⅰ类雨型的洪峰值。这是由于前期降雨需要使土壤达到饱和而下渗损失掉了,然后剩余雨量用于形成地表径流,恰恰第Ⅰ类雨型和第Ⅲ类雨型的雨峰靠前,其雨强较大时的降雨量多用于下渗来补充土壤水分,后续较小的雨量形成了地表径流。但是,设计雨型前期很长时段内雨量较小,该部分小雨量都用于补充土壤水分,当后续雨峰出现时,剩余雨量都用于形成地表径流,所以设计雨型的洪峰值要比第Ⅰ类雨型、第Ⅲ类雨型的偏大很多。因此,这也说明了雨峰出现越晚,洪峰流量就越大,汇流形成的洪水就会越危险,然而图集中的设计雨型恰恰是体现了洪水“峰高、靠后”的不利情况。
3.2 雨量预警指标结果分析
3.2.1 临界雨量计算
本文临界雨量计算方法采用水位流量反推法,该方法假定降雨和洪水频率相同,所以仅需要预警对象所在河道的控制断面地形资料信息,通过水力计算得到其水位~流量关系曲线,然后推求各预警时段成灾雨量。夏湾组水位~流量关系如图6所示,其中河道糙率n取值0.023,河道比降J取值0.055。由山洪灾害调查数据获取夏湾组成灾水位为281.46 m,对应的成灾流量为94 m3/s。

图6 夏湾组控制断面处水位流量关系Fig.6 Water level discharge relationship of XiaWan at control section
通过典型频率洪峰流量计算结果(表5)绘制洪峰流量与频率关系曲线,在该曲线上由成灾流量进行插值得到相应的成灾频率,再依据设计暴雨反算各时段临界雨量。土壤含水量为湿润情况(Pa=48 mm)下不同雨型的临界雨量结果如表6所列。
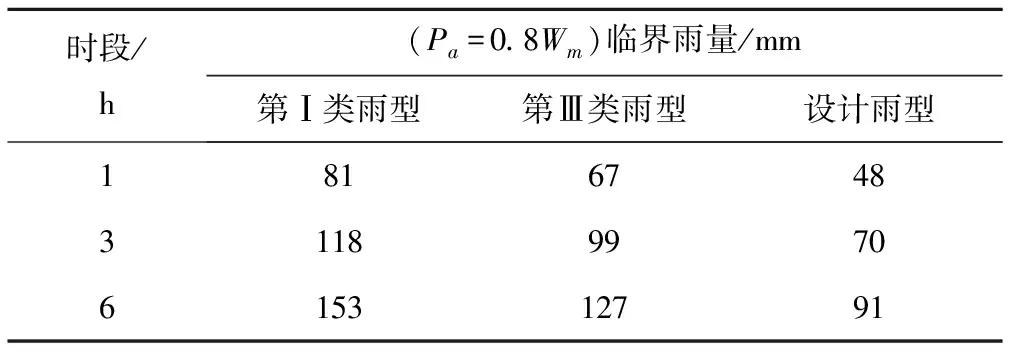
表6 夏湾组不同雨型对应的各预警时段临界雨量计算结果Tab.6 Critical rainfall calculations for each warning period in different rainfall patterns of XiaWan
准备转移雨量[20]是指山洪灾害发生但未成灾时,在合理的时间内组织人员撤离危险区而转入安全地带的雨量。准备转移雨量的计算也是基于洪水过程线,并且与洪峰流量有着密切关系。综合考虑预警对象所处河谷河段形态、洪水上涨速率、预警响应时间及站点位置等多因素,对夏湾组的成灾雨量进行折减处理,在成灾流量出现前0.5 h左右对应的流量经过反算相应的时段雨量,将该雨量作为准备转移雨量,如表7所列。
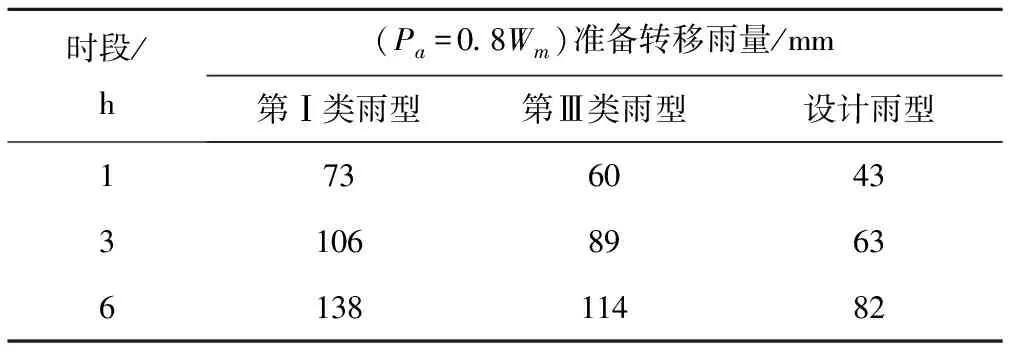
表7 夏湾组不同雨型对应的各预警时段准备转移雨量计算结果Tab.7 Preparation and transfer of rainfall calculation results for each warning period in different rainfall patterns of XiaWan
表6、表7结果表明,第Ⅰ类雨型对应的各预警时段临界雨量(或准备转移雨量)最大,而设计雨型对应各预警时段的临界雨量(或准备转移雨量)最小,结合设计洪峰流量结果可知,设计洪峰流量越大对应的临界雨量越小,如图7、图8所示。在同一预警时段内,不同雨型的临界雨量偏差可达到14~36 mm,准备转移雨量偏差约13~32 mm。因此反映出雨型对山洪灾害临界雨量的影响较大。
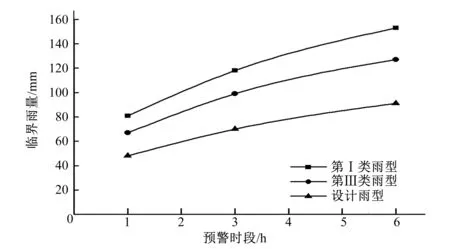
图7 夏湾组不同雨型对应的各预警时段临界雨量Fig.7 Critical rainfall calculations for each warning period in different rainfall patterns of XiaWan
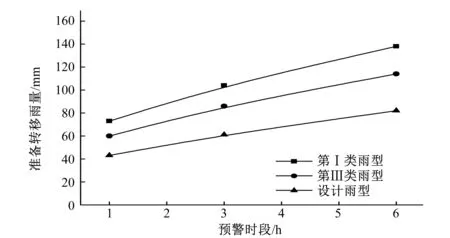
图8 夏湾组不同雨型对应的各预警时段准备转移雨量Fig.8 Preparation and transfer of rainfall calculation results for each warning period in different rainfall patterns of XiaWan
3.2.2 雨型对临界雨量影响规律分析
图集中设计雨型的雨峰偏后,并且在第1.2节中已知裴河小流域降雨特性是以雨峰偏前或居中的单峰型降雨为主。雨型的偏差会造成洪峰流量产生偏差,于是影响预警指标的精度。为了探究不同雨型与预警指标之间的响应关系,以图集中设计雨型作为裴河小流域“最不利”的降雨时程分布过程,引入偏差系数-B和偏差系数-M分别来估计雨峰偏前、居中时临界雨量比设计雨型的临界雨量偏大多少,将雨型对预警指标的影响进行量化。偏差系数可表示为:
(9)
(10)
式中:H1,t为雨峰偏前(第Ⅰ类雨型)时t时段临界雨量,mm;H3,t为雨峰居中(第Ⅲ类雨型)时t时段临界雨量,mm;Hsj,t为设计雨型t时段临界雨量,mm。这里需要说明的是H1,t、H3,t、Hsj,t分别为相同成灾流量所对应的t时段临界雨量。
为了使雨型与雨量预警指标之间的响应关系更好的适用于整个裴河小流域,而不是仅针对某个防灾对象。于是将成灾流量进行变化,分析不同雨型的偏差系数与成灾流量间的变化规律,如图9所示。
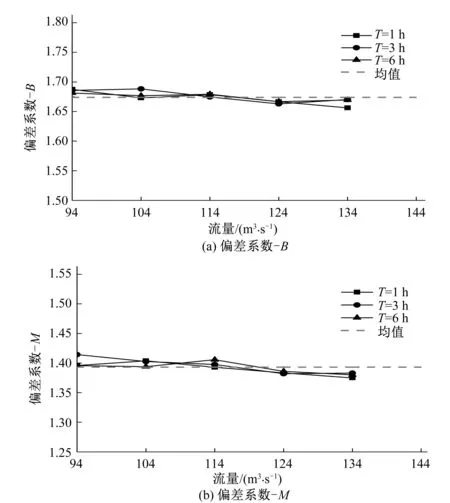
图9 偏差系数与成灾流量关系图Fig.9 Comparison of calculated transfer rainfalls in different rainfall patterns of the Xia Wan
图9表明偏差系数受到成灾流量变化的影响很小,偏差系数-B在均值1.67上下微小浮动,偏差系数-M在均值1.39上下微小浮动。不同成灾流量对应的偏差系数-B和偏差系数-M均在5%的变化幅度内,所以可以认为基本不变。因此,以设计雨型对应的临界雨量为基本预警信息,当出现雨峰偏前的降雨时,各预警时段临界雨量比基本预警信息偏大67%;出现雨峰居中的降雨时,各预警时段临界雨量比基本预警信息偏大39%。综合分析,裴河小流域的临界雨量会受到降雨时程分布的影响,导致各预警时段临界雨量具有不确定性,即1 h临界雨量为43~73 mm,3 h临界雨量为63~106 mm,6 h临界雨量82~138 mm,需要根据降雨时程分布情况来具体分析确定各预警时段临界雨量。
由以上结果,选取夏湾组2016年7月的一场成灾暴雨洪水,其暴雨编号为20160701,摘取该场次降雨的最大6 h降雨过程,总雨量可达166.5 mm,其雨峰位于第3时段,属雨峰居中。由该场实际降雨过程,产汇流计算其形成的洪水过程,当流量达到成灾流量时所对应的累计降雨量为160 mm,约6 h。将其总雨量通过暴雨图集中设计雨型进行时程分配,产汇流计算后,流量到达成灾流量时所对应的时段累积雨量为117 mm,约4 h。通过对比结果可知20160701场次雨峰居中的降雨所对应的累积降雨量是雨峰偏后的设计雨型所对应的累积时段雨量的1.36倍,接近上述得到1.39倍的结果。出现该情况是由于设计雨型及模式雨型都属于设计状态,与实际降雨过程会存在一定差异性。经实际降雨验证后表明,本文将雨型对临界雨量影响的定量化分析是具有一定合理性的,但实际应用中需要具体情况具体分析,并不能作为唯一确定的倍比值,可作为参考值。
综合以上不同雨型计算的临界雨量结果看出,雨型的不确定性对雨量预警指标的影响较大,导致雨量预警指标也存在不确定性。其次,雨型的雨峰位置越靠后洪峰流量越大,对应的临界雨量会越小,即雨峰所处位置与临界雨量大小呈负相关。根据20160701场次实际降雨过程成灾流量对应的时段累计雨量所用时间6 h,与设计雨型的时段累积雨量所用时间4 h对比可知,若实际降雨的雨峰出现时间早于设计雨型的雨峰时刻,则易导致空报;相反易出现漏报,造成严重损失。因此,山洪灾害预警预研究中,确定雨量预警指标时需要考虑雨型的合理性、可能性,应根据防灾对象所在小流域的降雨资料、降雨特性、计算精度等多方面要求,综合选择适宜的雨型推求方法,得出更接近小流域实际降雨过程的典型雨型,或利用实测降雨资料验证暴雨图集中设计雨型的合理性,弱化雨型对洪水及临界雨量的影响,从而提高雨量预警指标的精度,准确发布预警信息,减少空报、漏报的现象。
4 结 语
本研究通过模糊识别小流域最可能出现的雨型,在降雨特性分析基础上,结合图集中设计雨型,采用合理的产汇流方法和水位流量反推法,确定了预警对象的临界雨量和准备转移雨量,研究了不同雨型对雨量预警指标的影响程度,以及两者之间的响应关系。
基于不同雨型计算得到的临界雨量进行了对比分析,具体结论如下。
(1)山丘区小流域降雨在时间分布上并不是唯一的,具有随机性和不确定性。利用实测降雨资料模糊识别小流域降雨类型,发现出现频次较高的雨型与图集中设计雨型存在一定偏差,主要体现为雨峰位置不同,雨峰前、后雨强随时间的变化趋势有差别。
(2)基于多场次实测洪水过程建立了瞬时单位线模型,通过17场典型洪水对参数进行率定,2场典型洪水对模型进行了模拟验证,结果表明该瞬时单位线能够较好的模拟裴河小流域洪水过程,模拟值与实测值最大相对误差仅为7%,满足精度要求。通过设计洪计算发现,不同雨型得到的设计洪峰流量偏差较大,雨峰越靠后计算的设计洪峰流量越大,说明雨峰出现的位置对洪峰流量存在影响。
(3)土壤水分较湿润的条件下,即Pa=48 mm(0.8Wm)时,雨峰靠后对应的1、3、6 h内临界雨量比雨峰靠前、居中时的临界雨量偏小较多,雨峰位置对雨量预警指标的影响较大。分析得出裴河小流域夏湾组在降雨雨峰偏前时,各预警时段的临界雨量是设计雨型对应临界雨量的1.67倍;降雨雨峰居中时,各预警时段的临界雨量是设计雨型对应临界雨量的1.39倍。准备转移雨量可依据降雨前期土壤含水量及临界雨量的大小进行综合确定。
本研究有助于进行更合理的山洪灾害分析计算工作,研究结果也说明了雨型对雨量预警指标的影响较大,工作中需要考虑小流域雨型的合理性及适用性,从而提高山洪灾害预警指标的准确度。同时,研究内容也为开展山丘区山洪灾害预警指标检验复核工作提供新的切入点,具有一定的研究与应用前景,对山洪灾害预警的发展具有一定意义。但由于本文只针对具体小流域不同雨峰位置的单峰型降雨过程进行了研究分析,未考虑多峰型降雨,所以多样性雨型与小流域山洪灾害预警指标的影响规律有待于深入研究。
□

