一种针对时变干扰信号的空时抗干扰算法研究*
刘东辉,乔瑞萍
(西安交通大学电子与信息工程学院,陕西 西安710049)
0 引言
目前车载导航定位系统大多采用北斗导航接收机进行定位。由于导航信号的功率小,并且存在噪声干扰以及来自无线广播、恶劣天气等其他形式的干扰。脉冲干扰可用带通滤波器加以滤除,而对于带内干扰需要使用软件无线电技术进行处理以及自适应抗干扰处理[1]。在自适应抗干扰处理技术中有空域抗干扰,时域抗干扰以及频域抗干扰技术。目前的应用实例中,空时抗干扰技术已成为导航接收机主要的发展方向。本文分析了空时抗干扰技术架构,对基于空时抗干扰技术的高斯赛德尔算法,多级维纳滤波算法进行了研究和仿真[2]。高斯赛德尔迭代算法计算量小,利用序列数据对权值不断的迭代更新,完成对干扰信号进行处理,然而当干扰信号动态变化时,高斯赛德尔算法迭代时间较长,无法实时处理时变干扰信号。多级维纳滤波算法复杂度较高,利用等长度的数据块计算权值,然而当干扰信号改变时,多级维纳滤波无法对干扰信号状态(干扰功率、干扰方向、频率)转换处的信号进行处理。因此本文提出了高斯赛德尔算法和多级维纳滤波算法相结合的方法,实现了对时变干扰信号处理,并可以满足实时性的要求,更适应复杂多变的干扰环境。
1 空时抗干扰技术
1.1 空时滤波架构
空时滤波技术的核心思想是天线阵列对卫星信号进行空域采样,构成了空时抗干扰的空域部分。每个天线通道的横向延时构成了空时抗干扰的时域部分[2]。空时抗干扰首先根据天线阵列的各个阵元之间的相位差进行空域滤波,使某个方向的干扰信号得到衰减,然后对每个阵元接收的时域信号进行时域滤波处理,使某些频率的干扰信号得到衰减,从而达到了空时二维处理。空时滤波架构如图1所示。

图1 空时滤波架构
在图1中,导航信号以及干扰信号经过M 个天线阵元采集,并经过延时单元,输入到抗干扰信号处理板中,信 号 为 X = [x11,x12,…,x1k,…,xM1,xM2,…,xMk]。每个输入信号的权系数,即权值为W=[w11,w12,…,w1k,…,wM1,wM2,…,wMk]T。因 此 输 出 信号为y=WHX,通过权值W 完成了对导航信号的处理。
1.2 高斯赛德尔迭代算法
在一般情况下,GPS导航信号采用扩频形式进行传输。在传输过程中,噪声加干扰信号的功率比导航信号的功率强的多,卫星信号会淹没在噪声信号和干扰信号中,因此需要约束导航信号方向上wHS=1,调制其他权值使输出信号的功率最小,达到了干扰信号的抑制目的[3],即:
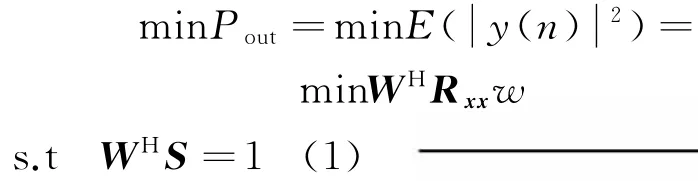
式中,Rxx为阵列接收信号(有用信号、干扰信号、噪声)的自相关矩阵,S=[1,0,…,0]T为约束矩阵,即约束第一个阵元的权值为1,由拉格朗日乘子法可得,权值:
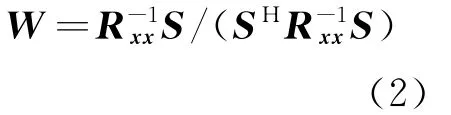
当干扰信号为平稳干扰信号时,1/(SHS)为定值,可假设权值为W=S,将公式左右同时乘以Rxx可得到权值求解式:

将公式两边都加上W可得:

可得权值迭代公式:

式中,C迭代算法的系数矩阵,I为单位矩阵。利用Guass-Seidel迭代法可表示为:
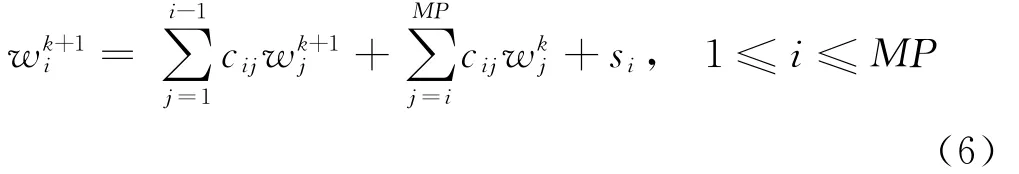
可得如下所示迭代格式:
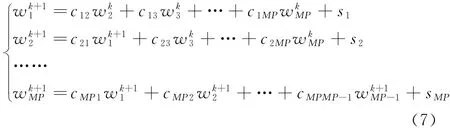
1.3 多级维纳滤波降维算法
在导航信号的方向未知的情况下,假设天线阵列第一个阵元收到的信号为期望信号d0(k),设存在权值W使输出信号WHX0(k)与期望信号d0(k)的误差e(k)最小,即:
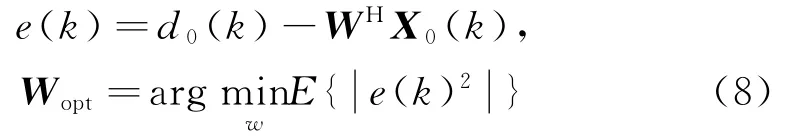
通过最陡下降法,根据E(e(k)2)/W =0,可得到空时自适应滤波权值为:

对式(9)需要进行矩阵求逆运算,计算量较大,在实际工程应用中会造成设备成本较高,因此考虑使用多级维纳滤波器进行实现[4]。多级维纳滤波器分为前向递推与后向解析过程,其结构如图2所示。
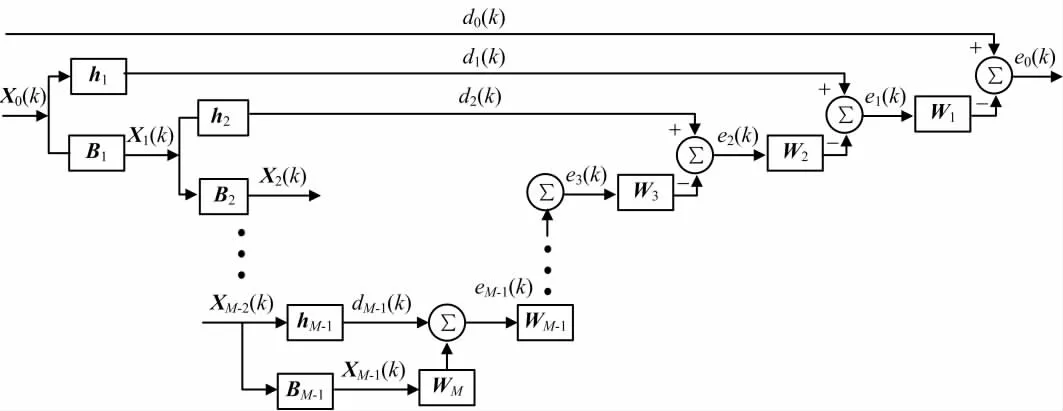
图2 多级维纳滤波器
前向递推过程利用选通矩阵hk和阻塞矩阵Bk将输入信号分解为期望信号d(k)和不含期望信号的信号x(k),通过前向递推的多级分解将输入信号分解不含干扰信号的导航信号,此时前向递推滤波器完成了信号的前向分解作用[4]。在后向解析滤波器中,通过对每一级的分解的误差向量与上一级期望向量的运算得到了每一级分解的权值Wd:
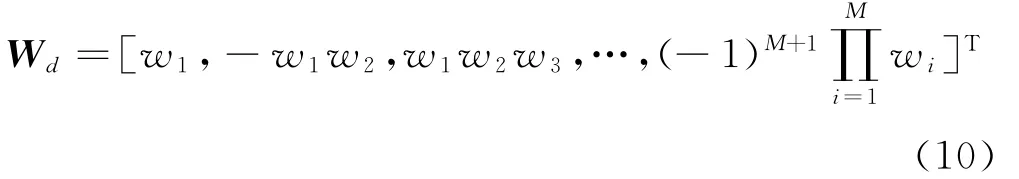
并通过与选通矩阵与阻塞矩阵进行运算得到了多级维纳滤波权值:
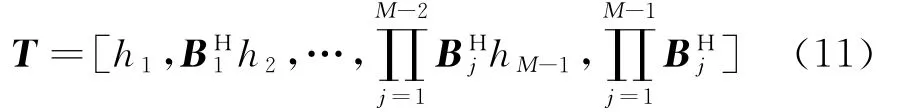
多级维纳滤波器等效权值:

1.4 结合算法
在动态干扰环境中,由于干扰信号的参数发送变化,高斯赛德尔算法收敛较慢,不能有效地处理实时信号。多级维纳滤波算法求解权值需要计算一定长度的数据块,在干扰信号状态(功率、干扰方向、频率)转换的时间段里,多级维纳滤波算法不能对干扰信号有效处理。本文针对时变干扰信号的特点,结合高斯赛德尔迭代和多级维纳滤波算法,提出了高斯赛德尔迭代算法和多级维纳滤波算法相结合计算权值的的方法。结合算法流程图如图3所示。
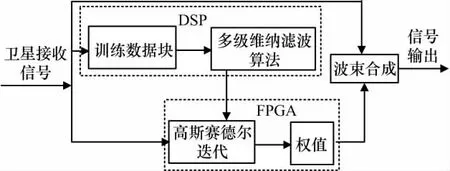
图3 结合算法流程图
结合算法计算权值步骤为:
1)将接收信号分为三个支路传输到抗干扰算法处理模块。其中一个支路是将接收信号以数据块的形式传输到DSP里。在DSP里利用数据块计算多级维纳滤波算法权值;
2)同时另一支路数据实时的传输到在FPGA里,并在FPGA里利用高斯赛德尔迭代算法逐点计算权值WGS,使用权值WGS进行波束合成,得到空时抗干扰输出信号y=X;
3)在DSP支路计算出多级维纳滤波算法权值Wmwf后,将该权传输到FPGA里。在FPGA里将更新并在权值Wmwf的基础上继续进行迭代更新,利用多级维纳滤波算法权值提高了高斯赛德尔算法迭代速度,使权值WGS快速达到局部最优解,并进行波束合成,得到输出信号Y=X;
4)不断循环上述3个步骤。
2 算法仿真
在对空时抗干扰算法理论分析后,需要对每种算法进行性能验证。首先给出本文的仿真环境;假设采用均匀圆阵进行仿真,阵元数M 为4,抽头数P为5,阵元延时为3,阵元中心距为0.5λ。干扰信号为三段多音干扰信号,每段干扰信号由3个不同干扰方向的多音信号组成。每段干扰信号的干噪比,干扰方向,干扰频率随时间变化,具体参数如下表1所示。

表1 时变干扰信号参数
在表1的时变干扰信号仿真环境下,高斯赛德尔迭代算法,多级维纳滤波算法以及结合算法仿真结果如图4所示。
观察图4(a)输出信号功率图,当干扰信号动态变化时,高斯赛德尔算法收敛较慢,最优权值的迭代过程较长,不能有效地对干扰信号进行处理。在干扰信号状态(干扰方向、干扰功率)转变的时间段里,即在每段干扰信号前端部分,多级维纳滤波算法不能有效地对该段干扰信号进行处理。
通过图4(b)的局部输出信号功率图,在干扰信号状态转换的时间段里,结合算法利用高斯赛德尔迭代算法对该段干扰信号进行处理。对于该段时间里的干扰信号,可以进行一定程度的抑制,仿真效果与高斯赛德尔算法仿真效果相同。同时当多级维纳滤波算法计算出权值后,该权值会被更新为高斯赛德尔算法权值,并在该权值的基础上进行迭代,提高了高斯赛德尔算法收敛速度。对于后续的干扰信号,可通过最优权值进行处理。通过仿真和分析可得:本文提出的结合算法能够结合高斯赛德尔迭代算法和多级维纳滤波算法优势,有效地对时变干扰信号进行抑制。

图4 算法仿真结果
3 硬件仿真
3.1 OMAPL138双核协同仿真
本文采用基于OMAPL138芯片的双核协同仿真架构进行算法移植,其中ARM芯片为主处理器,DSP为32位浮点型协处理器,在实际应用中ARM大多作为系统的调度和设备管理,DSP负责算法处理和数据处理[5]。
双核协作工作过程为ARM使用ProcMgr_Write组件[6]将仿真数据写进DSP内存中,并使用Notify函数通知DSP进行算法处理。DSP接收到Notify通知后从内存中读出仿真数据并进行数据的重组,并调用抗干扰算法计算权值,算法执行结束后,DSP给ARM发送Notify算法完成通知。ARM端接收到DSP的算法完成Notify通知后,使用ProcMgr_read组件从DSP内存中读出权值并通过RS232串口将数据传输到主机上,在主机上利用Matlab绘制出DSP硬件仿真输出信号功率演变图。综上所述双核协同仿真架构如图5所示.
3.2 实现结果
硬件仿真环境采用第2节的仿真环境,仿真数据为MATLAB仿真时变干扰信号数据。分别对三种算法进行DSP移植,并绘制出输出信号功率图如图6所示。
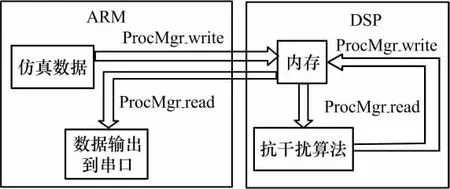
图5 双核协作仿真架构
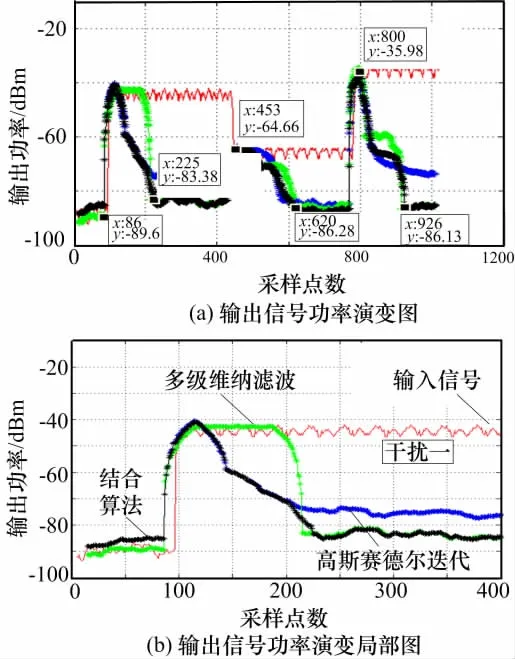
图6 DSP仿真功率输出图
仿真分析:一般车载导航系统对于接收机抗干扰算法的最大反应时间为100ms。根据抗干扰算法对干扰信号的反应时间t的计算公式t=(xlastxfirst)/fs,式中xfirst表示输出信号中存在干扰信号的第一个采样点,xlast表示输出信号中干扰信号完全被抑制的第一个采样点。fs表示输出信号的采样频率(62MHz),由图6(a)的输出信号功率演变图可得,结合算法的对干扰信号的反应时间为2.323ms,能够满足车载导航系统对抗干扰算法的实时性指标。同时结合图6(b)的输出信号功率局部演变图,可得结合算法能够对时变干扰信号的硬件仿真效果相对高斯赛德尔迭代算法、多级维纳滤波算法性能较好。
4 结束语
本文针对空时抗干扰技术进行了阐述,并对高斯赛德尔迭代算法,多级维纳滤波算法进行了理论分析和仿真验证。提出了针对时变干扰信号可利用多级维纳滤波算法与高斯赛德尔算法相结合的算法。通过时变干扰信号仿真验证,结合算法能够有效的对时变干扰信号的进行处理,且具有实时性好,干扰抑制能力强的特点。同时本文对三种算法进行了DSP硬件仿真,验证了结合算法的硬件移植效果,完成了算法的硬件实现,为实际工程应用奠定基础。■

