对星近距随遇悬停的可行性初探
王灏宇,陈 粤,齐维孔
(中国空间技术研究院通信卫星事业部,北京100094)
0 引言
目前,中低轨道、同步轨道上分布着众多各国军用、民用卫星。对在轨卫星的近距抵近可以开展详查监视、在轨维护与操作。在航天器检查与维护、部件替换和交会对接等多项在轨服务任务中,经常会使用“悬停”技术,使任务航天器相对于目标航天器在指定坐标系中,长期稳定地静止于某个固定点,以增强任务执行的安全性与可靠性[1]。
国内外对悬停技术已经具有共识的结论是[2-5]:严格意义的悬停需要抵近航天器采用能够提供连续可变推力的发动机,以及目标航天器各时刻的位置和方位角信息。
由于航天器采用连续可变推力发动机的工程难度大,Hope和Trask[6]提出了一种使任务航天器以“雨滴”形轨迹的方式实现在目标航天器轨道平面内近似悬停的构想。饶殷睿和韩潮[7]设计了可使任务航天器在目标航天器轨道平面外和平面内悬停的“雨滴”悬停轨道,并给出了清晰合理的构型描述方法和控制策略:间歇式的脉冲控制策略。
间歇式的脉冲控制策略依靠发动机间歇式点火提供速度增量,一方面使得悬停时间受限于燃料消耗;另一方面也只可实现一定区域内的相对近距悬停,并非严格的相对静止[6-7]。这种悬停方式在超近距离(距目标15m范围内[8])悬停任务中,无法为在轨维护等精细操作建立长时间的相对静止条件。
本文提出抵近星平台采用连续推力作用下进行近距离(100m~1m)任意定点悬停(称为随遇悬停)的抵近控制方案,长时间的连续推力可由一种新型的连续可变推力发动机:无质损电磁推力器实现。这种控制方案可为在轨操作、详查监视等提供长时间相对静止条件,进一步可大大牵引多种在轨操作手段,提升在轨服务效能。
文章首先分析了抵近星悬停的理论可行性,包括在目标星近域内的平衡点的存在性分析和基于连续推力的可控性分析。接下来分析了抵近星在近距离悬停控制中所需的连续推力特性。然后调研一种新型的连续可变推力发动机:无质损电磁推力器的性能,初步分析了将其用在近距、任意点悬停的可行性。最后,分析了抵近悬停任务对抵近星的能力需求。
1 悬停可行性分析
1.1 平衡点的存在性
悬停要求抵近星在目标星附近达到平衡,从而保持相对静止。抵近星在目标星附近的动力学方程可由C-W方程描述,平衡点也可由C-W方程的解描述[9]。
如图1所示,以同步轨道通信卫星飞行姿态为例,坐标系中心位于目标星中心,X轴沿地心矢径方向,Y轴沿目标星轨道速度方向(指向东),Z轴垂直于轨道平面指向北极方向。抵近星的坐标可表示为(x y z)T。
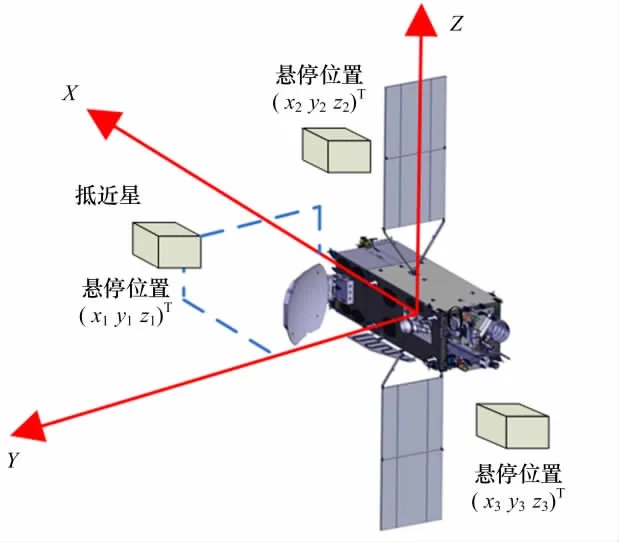
图1 目标星轨道坐标系
设目标星不受摄动力和控制力,抵近星不受摄动力,仅受控制力,控制力在轨道系下为:Fs=(FxFyFz)T,则抵近相对运动方程为[9]:
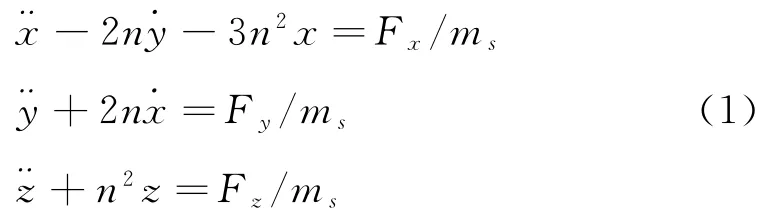
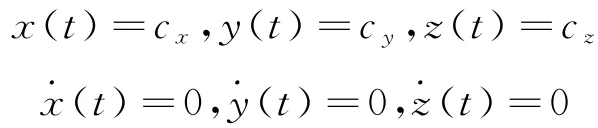
所需要的轨道保持力为[10]:
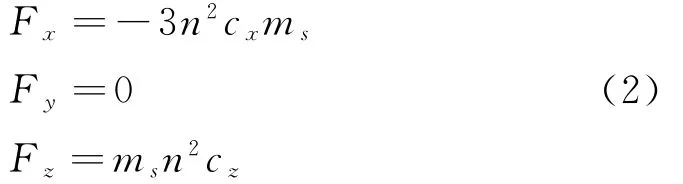
式(2)说明,在不计扰动的情况下,对于任意相对位置的定点悬停要求,存在定常的轨道控制力可以用于定点保持,即随遇悬停是可行的。此外可以得出结论:1)悬停所需保持力仅沿X 轴向和Z轴向;2)保持力的大小与质量成正比;3)保持力的大小与相对距离成正比。
1.2 基于连续推力的悬停可控性分析
将x(t)=(x(t)y(t)z(t)x(t)y(t)z(t))T视为状态量;控制起始的某初始时刻处于任意点的平衡位置,有x(0)=(x0y0z0x0y0z0)T,代入到相对运动动力学方程,得到:
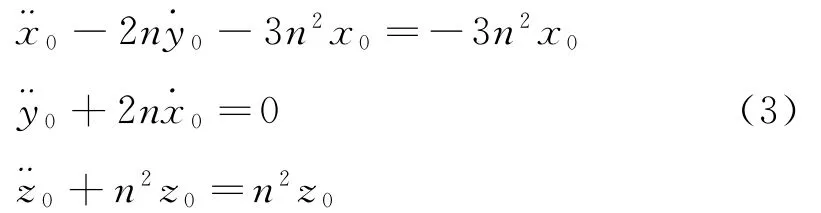
将(1)、(3)两式相减,得到:
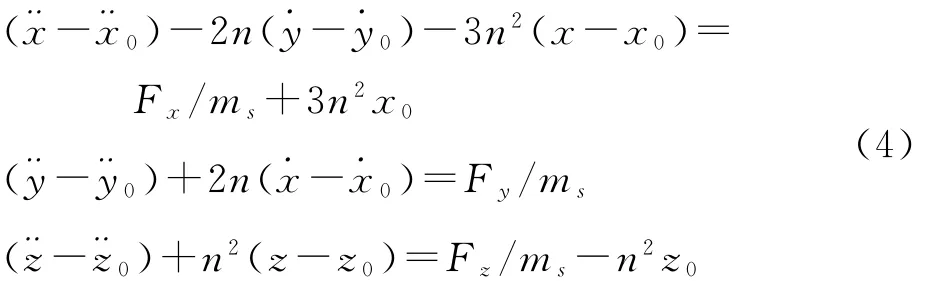
下面将式(4)转换为状态方程,令xe(t)=x(t)-x(0)(t)=(t)-(0),设系统控制输入为u=(FxFyFz)T,在此输入的作用下希望抵近星保持在某一初始位置:x(0)=(x0y0z0)T处附近,系统的状态方程为:
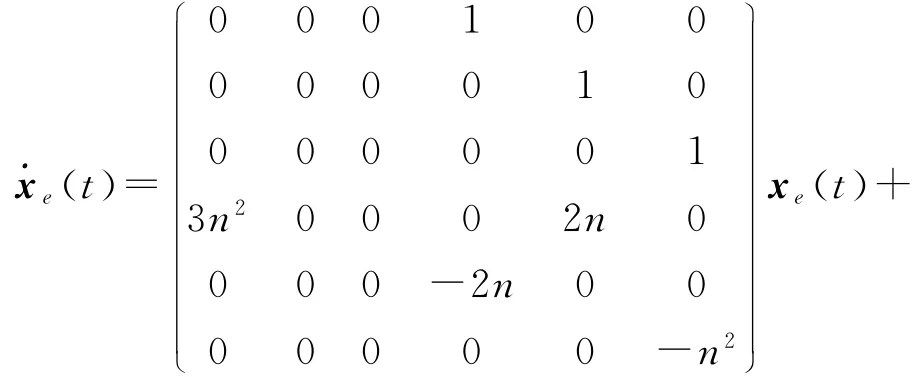
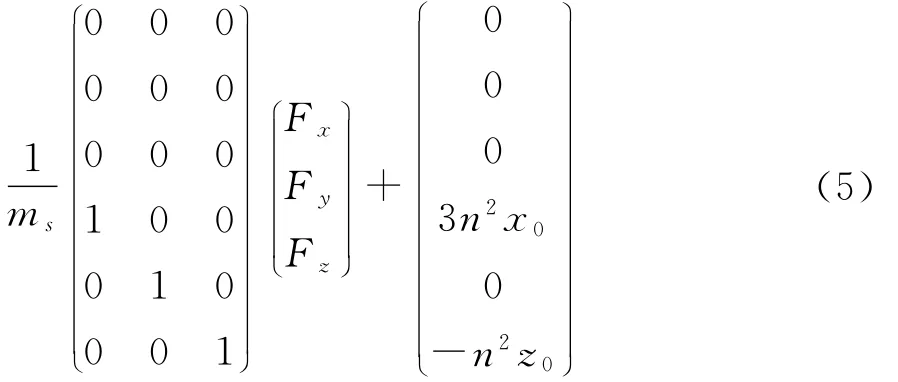
根据状态方程的特征值分析,可见本身在平衡点是不稳定的[11]。此外,(0 0 0 3n2x00 -n2z0)T项可作为控制系统的定常扰动(仅与目标位置相关);当抵近星在x(0)除保持平衡时,因此抵近星需要具有连续推力 ms(-3n2x00n2z0)T,以抵消定常扰动,称之为保持平衡的常值项(以下称:常值项)。常值项具有的特点为:1)不间断的连续性和2)定常性:仅与期望的保持位置相关。
令常值项推力:
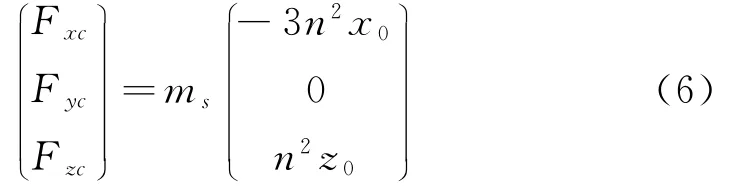
以及令:u′=(F′xF′yF′z)T为反馈控制量,则输入控制可分为反馈控制量和保持平衡常值项的加和:
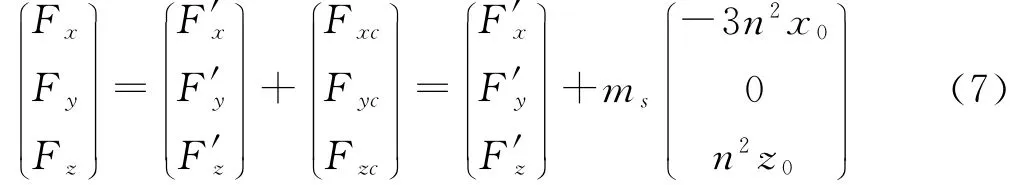
则状态方程演化为:

可知系统能控性矩阵和能观性矩阵均满秩。系统即能控又能观。可以设计系统的线性状态反馈控制器,令系统的控制输入具有状态反馈形式:
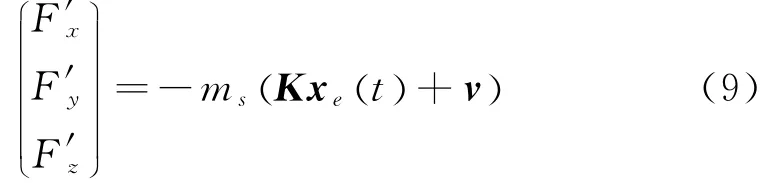
K为反馈系数矩阵。则状态方程演化为:
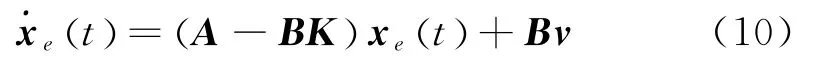
式中,

从以上分析可以看出,u′=(F′xF′yF′z)T反馈控制量具有的特征为:1)具有连续性特征;2)控制推力为变推力。
结合式(7)分析,抵近星的推力控制需求为:1)长时间的连续推力;2)推力大小可变。推力应由两部分组成:反馈变推力和常值项推力。在此种控制推力的作用下,抵近星的近距离悬停是可控的。
2 近距悬停控制的连续推力需求分析
由于所需的控制力由反馈变推力项和常值项推力的加和组成,在计及扰动时,抵近星所需的连续推力需求还应考虑椭圆轨道因素和摄动因素。
2.1 常值项推力量级分析
单位质量的抵近星所需要的常值项有(-3n2x00n2z0)T的形式,与目标星地心距和悬停位置的X向、Z向距离有关。令单位质量的常值项推力具有如下形式:
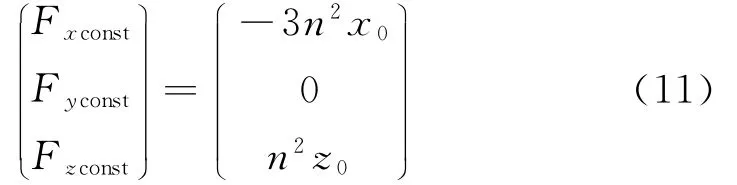
显而易见,单位质量的常值项推力与悬停位置的X向、Z向距离的关系为线性相关,且相互独立。单位质量的常值项推力随目标星的地心距的关系如图2所示。
从图2可以看出:1)在一定轨道高度,Fxconst、Fzconst随悬停的距离增大而线性增加;2)若需要保持一定悬停距离,Fxconst、Fzconst随着轨道高度的升高而降低。考虑式(6),有:
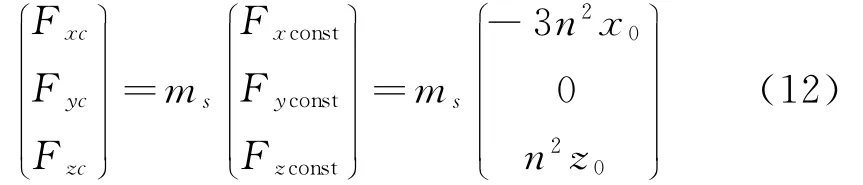
常值项推力仅分量Fxc、Fzc存在分量。Fxc、Fzc除具有与Fxconst、Fzconst一致的特性之外,还与抵近星质量线性相关。表1比较了不同抵近星质量的条件下,Fxc、Fzc在近地轨道和同步轨道的量级变化。
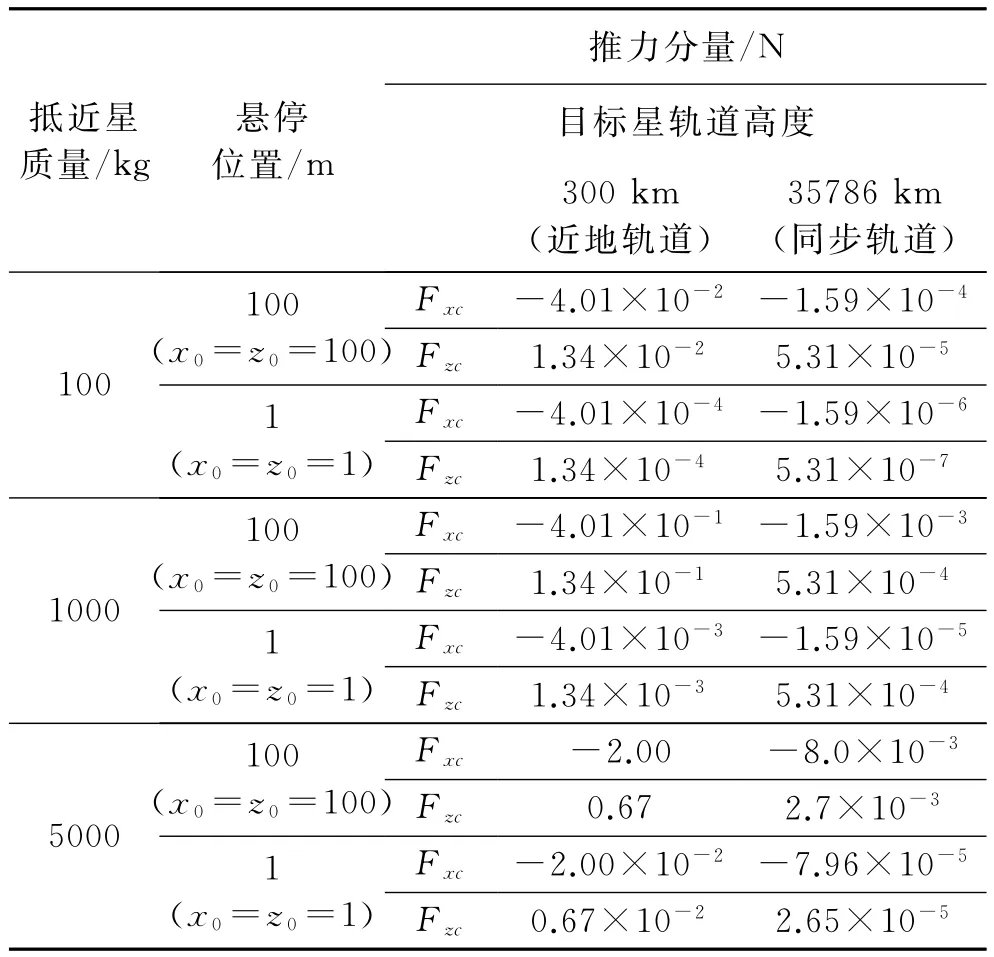
表1 不同抵近星质量的条件下,Fxc、Fzc在近地轨道和同步轨道的量级
2.2 椭圆轨道因素分析
椭圆轨道情况下,式(1)中的n应被替换为;n=(μ/r3m)1/2,其中,rm表示目标星的瞬时的地心距[10]。由式(11)可知,Fxconst、Fzconst随目标星实时地心距时刻变化,满足:
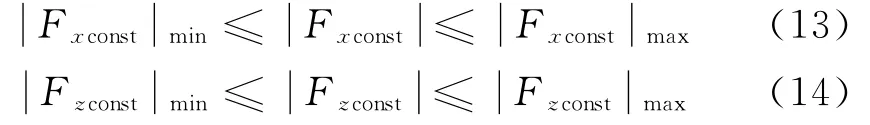
由前述分析已知,Fxconst、Fzconst的大小在同步轨道高度达到最小值,在近地轨道高度达到最大值,因此可认为:
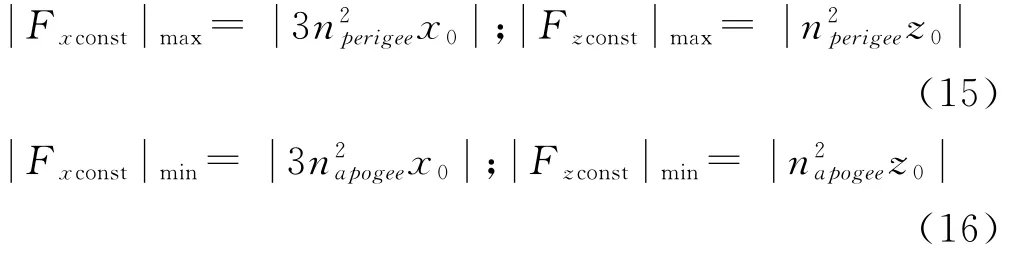
式中,nperigee= (μ/)1/2,rm_p为目标星在椭圆轨道近地点的地心距;napogee= (μ/a)1/2,rm_a为目标星椭圆轨道远地点的地心距,最远不大于同步轨道卫星的地心距。
因此,在目标星轨道为椭圆轨道,并且近地点高于300km的情况下,Fxc、Fzc将分别在表1所示的每一项悬停位置的最大、最小值之间变化。
2.3 摄动因素分析
抵近星受到扰动力,会偏离需要的平衡位置。在轨航天器受到的扰动力包括地球J2项摄动、月球引力、光压力等,其中地球J2项摄动的影响较为明显[11-13]。
对于相对近距悬停的轨道控制,影响抵近星偏离平衡位置的扰动力主要由地球J2项摄动力施加在目标星和抵近星两者的差产生[10]。由于抵近星在目标星附近很小范围内(100m内)悬停,地球J2项摄动施加在目标星和抵近星的差别,与星间近距悬停所需的作用力相比很小,故可认为在悬停保持时,将引起抵近星偏离某平衡位置的扰动力很小[10-13]。
日、月对于同步卫星的摄动力与地球中心引力之比[14]分别是0.75×10-5和1.63×10-5。100m 近距域内,抵近星的地心距和目标星的地心距的差达到最大值100m 时,有:rs=rm±0.1km,此时太阳摄动力在抵近星和目标星上引起的加速度的差为:
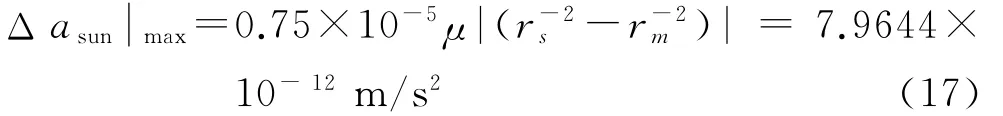
同理,100m近距域内,抵近星由于受到月球摄动力引起的加速度差最大为:
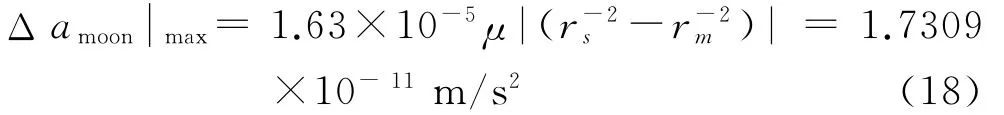
结合前述分析的式(5),可知在考虑摄动因素条件下的状态方程为:

可见,有日月摄动力引起的加速度与近距悬停所需的连续推力引起的加速度相比具有较小的量级(以100m处近距悬停为例,连续推力引起的加速度为10-6m/s2量级,见表1),在研究动力学控制时(见式(8))将日月摄动力视作小量级的扰动予以忽略是合理的。
综上,在进行近距悬停的动力学分析时,地球J2摄动和日月引力摄动可以视为小量级扰动予以忽略。
2.4 反馈变推力项量级分析
结合式(7)~(9)分析,在不受到扰动时,除常值项之外,抵近星还需要反馈控制推力纠正位置偏差。由于抵近星此时在平衡位置悬停,不会产生位置偏差,可认为此时反馈控制推力为零。在抵近星受到小量级的扰动之后,反馈控制推力纠正由小量级的扰动引起的位置偏差,在长时间的悬停过程中,反馈控制将体现出利亚普诺夫渐进稳定的效果[14],抵近星将保持在平衡位置附近小的临域之内,可认为反馈控制推力与扰动力是处于同量级的。
综上,连续推力应能提供近距悬停控制所需的主要部分:常值项推力。常值项推力量级与悬停位置和目标星实时的轨道高度相关(见表1)。
3 近距悬停应用无质损电磁推力器的可行性
目前,能够产生连续推力的推力器种类主要是电推进(离子推进)器。电推力器产生推力比冲高,可长时间连续工作。由于采用电推力器可大大减少燃料质量,现主要用于同步轨道卫星,其电推力用于长期近距悬停和入轨阶段的转移轨道的轨道控制。离子推进的原理为:依靠喷出的带电粒子产生反作用力,所携带的工作介质会随着近距悬停时间的增加而逐渐消耗。电推进装置需要携带庞大的工质储箱,还存在羽流干扰问题。因此有理由预见,电推力器也可以提供一段时间以内的相对静止近距悬停所需推力。
相比之下,一种不需要消耗燃料或工质的推进器被称为:无质损电磁推力器[15]。
无质损电磁推力器是一种全新的概念。在相应的推进装置中,微波通过波导被辐射进封闭的圆台型推力器腔体后作用在腔体表面上,并沿推力器轴线产生净推力。这种推进装置的特点是:1)不需要工作介质就可以产生净推力;2)只要微波输出电功率稳定,推进装置的性能不受工作环境的影响,可以产生长时间连续推力;3)没有高温燃气流的烧蚀、冲刷和传热问题,结构简单,能大幅度降低热控需要的设备和其他结构质量[15]。
已有的部分试验和理论分析表明采用不同的推进装置结构材料,在1kW微波功率输出条件下,可以获得0.1~31500N范围的推力[16]。2009年Shawyer在2.9kg的谐振腔体上实际测量:在300w微波输出功率的直接作用下,谐振腔产生了86.2mN的推力[17]。2014年,NASA的David A Brady等对谐振频率1.933GHz、微波功率17W 的圆台谐振腔微波推力装置,利用扭摆法测得91μN的平均推力[18]。2016年发表的最新研究成果[19]表明,向无质损微波推力器馈入60W的电功率,可得到0.1mN净推力;推力器的能力可以达到1.2mN/kW,远远大于其他无质损推进器如激光推进、太阳帆推进,以及离子推进的0.0033~0.0067mN/kW的推力水平。中国空间技术研究院已经完成了无质损电磁推力原理样机试验,指标达到0.1 mN/20W,考虑到微波器件的电功率损耗,推力器产生0.1mN量级推力时,需要的电功率为40W。处于国际先进水平。未来中国空间技术研究院将研制40mN/400W的无质损电磁推力系统,系统包括:热控回路、高效集热系统、低温制冷系统、微波系统、控制器、推力器等,系统质量在100kg以内。
根据中国空间技术研究院研制的无质损电磁推进技术原理样机的性能,将近距悬停推力需求与推力器能力对比如表2所示。由于同步轨道卫星具有对地定点的特点,同步轨道卫星多为对地观测类和对地通信类的卫星,这类卫星提供实时不间断服务,对于提供服务的间断时间非常敏感,因此对同步轨道卫星的近距离在轨维护显得颇为重要。表2对比分析了同步轨道上微纳抵近星(100kg)和大型抵近星(5000kg)近距悬停所需的电功率、单个推力器质量和单个推力器推力。
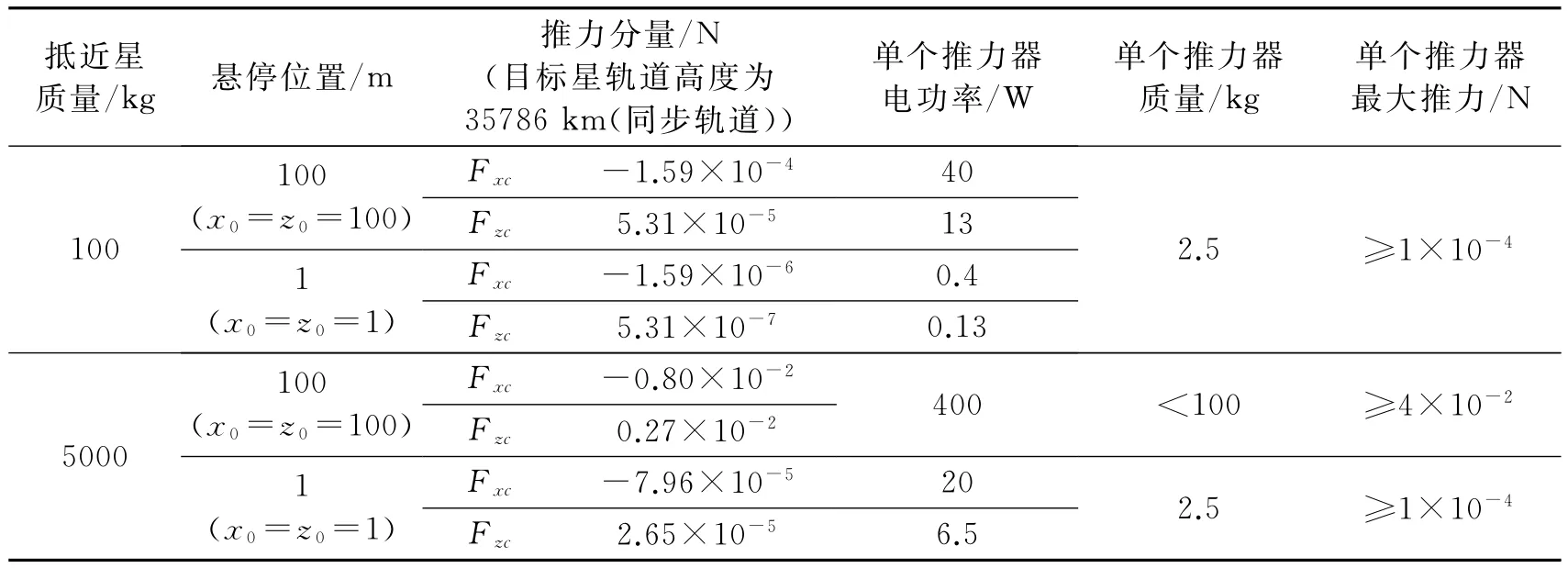
表2 近距悬停推力需求与无质损电磁推力器能力对比
同步轨道通信卫星平台如美国A2100平台、B702平台可提供的整星功率都在10kW量级,若以同步轨道大型卫星平台为基线设计抵近星,可以预计无质损电磁推力器能够满足100m范围内的近距悬停需求。
若将同步轨道上的抵近星设计为微纳星,需要微纳星提供悬停专用的电功率为53W以内(见表2),按照三结砷化镓太阳能电池板的240W/m2性能估算,对应的提供此部分电功率的专用太阳能电池板为0.22 m2以内。尽管仍然可以进一步进行质量与功率的优化设计,但是初步估计100kg级的微纳星携带大于0.22m2的太阳能电池板是合理的。
由表2可见,无质损电磁推力器的初步研究已经表明,其已经能够满足:1)大型抵近星(质量5000kg级)对同步轨道目标的近距离悬停需求;2)微小型抵近星(100kg级)对同步轨道目标的近距离悬停需求。
对于中、低轨道的目标卫星,虽然尚无明确针对性的研究证明应用推力器进行近距离悬停控制的可行性,但是随着相关研究进展,推力器的推力增加,可以继续跟踪研究进展并提出抵近悬停推力需求作为牵引。
综上,可以得出初步的分析结论:1)与经典电推力器相比,无质损电磁推力器在产生长时连续推力方面更具优势;2)对无质损电磁推力器的初步研究成果分析可以认为,其推力量级满足同步轨道近距悬停控制的连续推力需求。此外,针对近距悬停任务,尚需要进一步明确推力器设计的指标要求。
4 同步轨道抵近悬停任务要求
4.1 同步轨道目标几何特性
以对同步轨道卫星进行抵近在轨维护为例,GEO带内卫星主要包括通信广播卫星、数据中继卫星、导弹预警卫星、电子侦察卫星等应用卫星。
同步轨道卫星的共性特点为:1)本体长宽在1.5~3m范围内,高度在2~8.5m范围内;2)具有南北向展开的太阳能电池板;3)东西板和对地板布置有对地的天线或观测设备。
4.2 悬停位置
根据美国凤凰计划,天线或对地观测设备可能成为在轨维护的主要对象。因此,抵近星应尽可能靠近天线或观测设备。距离天线或观测设备1m以内。
在抵近过程中,可能会途径正常工作的天线的对地主瓣或观测设备的对地视场,进而会产生一定遮蔽作用。因此需要合理规划近距离检查、悬停的路径,合理规划多个悬停位置,以及多个悬停位置之间的机动路径。
4.3 抵近星能力需求初步分析
抵近悬停可用于在轨维护等空间操作,抵近星应具备满足近距详查巡视要求的相对位置控制能力。就悬停而言,抵近星悬停位置的决策由地面指挥人员通过检视目标星表面特征后作出,抵近星悬停的控制由星上完成。因此需要能力为:
1)三维相对空间位置测量能力
抵近星需要实时获取相对目标星的位置信息以作悬停或近距离详查激动地控制反馈。由于抵近星在目标星附近机动或悬停时,受到连续推力的持续作用,其轨道为非开普勒轨道,为得到其相对于目标星的三维空间位置,需要进行相对测量。
首先需要建立相对位置的数学描述方法。为服务于相对近距悬停控制,相对位置的数学描述必须在目标星轨道坐标系下进行。相对测量的手段可以采用地面测量目标星和抵近星在地球固连坐标系下的位置,解算得到目标星轨道坐标系下的相对位置矢量;也可以采用抵近星自主测量相对位置矢量。两种手段可互为备份。
关键点在于:①在抵近星上建立目标星轨道坐标系的基准信息,这种目标性轨道坐标系信息可由地面等空间态势感知系统或天基非合作目标测量手段测量得到并上传至抵近星;②抵近星须获得自身的实时的姿态信息;③抵近星须具有对目标星的方位和距离测量能力。
2)对地受遮挡条件下的高轨道星地高速图像数传能力
抵近星在近距离详查和维护操作时需要将实时图像下传以供地面人员研判和指挥。当抵近星在目标性被地面详查或操作时,对地通信可能受到目标性遮挡。当目标星对地通信观测过程中,抵近星下传链路还可能与目标星对地通信连路发生干扰。
3)视场受限条件下的长时姿态测量能力
当抵近星在目标星近距离详查或操作时,姿态测量装置如:星敏感器、红外地球敏感器、太阳敏感器都有可能受到目标星的遮挡。如果采用惯性姿态测量设备如陀螺则需要解决长时间悬停中的零点漂移问题。因此需要解决敏感器与陀螺的交替配合使用策略,或采取相对于目标星的相对姿态测量。
4)连续推力能力
抵近星近距离悬停需要连续推力。可由新型无质损电磁推力器实现。
后续仍需要在深化抵近星能力要求的基础上开展抵近星的总体方案设计。
5 结束语
本文分析了近距离随遇悬停的平衡点的存在性和可控性,分析了抵近星近距悬停的连续推力需求。调研了可产生连续推力的推力器:新型无质损电磁推力器的技术性能,比对分析了将其应用在近距悬停任务的可行性,最后分析了抵近悬停的任务要求。本文得出以下结论:依靠长时间、连续、可变推力进行近距离范围内任意点悬停是可行的;近距悬停所需的连续推力主要体现为沿目标星轨道坐标系X、Z向的常值项推力,常值项推力大小具有与悬停位置和目标星实时的轨道高度相关、与悬停距离成正比、与抵近星质量成正比等特性;无质损电磁推力器能够满足同步轨道近距悬停控制的推力要求;同步轨道近距悬停对抵近星的能力和总体方案提出了不同于其他卫星的要求,需要进一步分析。■

