小型涡扇发动机低压转子临界转速随支承刚度和悬臂长度的变化规律研究

袁 胜 ，邓旺群 ，徐友良 ，刘文魁

(1.中国航发湖南动力机械研究所，湖南 株洲 412002；2.中国航空发动机集团航空发动机振动技术重点实验室，湖南 株洲 412002)

1 引言

中小型航空发动机转子正朝着高转速、细长、柔性的方向发展，其高速转子动力学问题日益突出，正成为制约发动机研制的一个关键因素。许多学者在航空发动机转子动力学领域开展了大量的研究。邓旺群等[1-5]对涡轴发动机动力涡轮转子的动力特性进行了系统的理论分析和试验研究，分析了传动轴、测扭基准轴和动力涡轮盘这三个主要零部件对转子动力特性的影响，对不同支承刚度条件下小型涡扇发动机非悬臂低压转子的临界转速进行了系统的计算分析。孙涛等[6]对带挤压油膜阻尼器的悬臂转子进行了动力学瞬态与稳态响应的研究，并分析了转子轴直径与悬臂长度变化对转子瞬态响应和转子临界转速的影响。李海伟[7]基于有限元法建立了转子的有限元计算模型，分析了转子临界转速随支承主刚度与主阻尼的变化规律。邓旺群等[8]对不同支承刚度、轮盘质量、低压轴壁厚条件下涡桨发动机低压转子的临界转速进行了系统的计算分析。聂卫健等[9]以小型涡扇发动机非悬臂低压模拟转子为研究对象，研究了前三阶临界转速随各支承刚度、各轮盘质量的变化规律。邓旺群等[10]还研究了对转发动机低压转子临界转速随支承刚度和轴向位置的变化规律。

合理设计临界转速是保证发动机安全、可靠运行的前提，所以在设计转子时应使其临界转速合理分布，使得在一些转速范围内不出现临界转速或使临界转速远离转子的工作转速。为有效调整转子临界转速，通常通过选取合适的支承刚度、合理的质量分布及优化转子结构等措施来实现。某小型涡扇发动机低压转子是一个超两阶弯曲临界转速工作的高速悬臂柔性转子，本文以其为研究对象，建立了该低压转子的有限元计算模型，并在不同支承刚度和不同悬臂长度条件下对低压转子的前三阶临界转速进行了系统的计算分析，揭示了前三阶临界转速随支承刚度和悬臂长度的变化规律，可为低压转子临界转速设计和调整提供理论依据。

2 低压转子结构

低压转子的结构示意图见图1。该转子具有空心、薄壁(壁厚 2.5 mm)、大长径比(长径比大于 20)、风扇端悬臂的结构特点，是一个典型的带细长轴的悬臂高速柔性转子。转子主要由风扇盘、低压涡轮盘、低压轴及进气罩等零部件组成，采用0-2-1支承方式。其中，1号轴承为滚珠轴承，2号和5号轴承为滚棒轴承，轴承编号与发动机中的轴承编号一致；支承位置均有鼠笼式弹性支承和挤压油膜阻尼器。

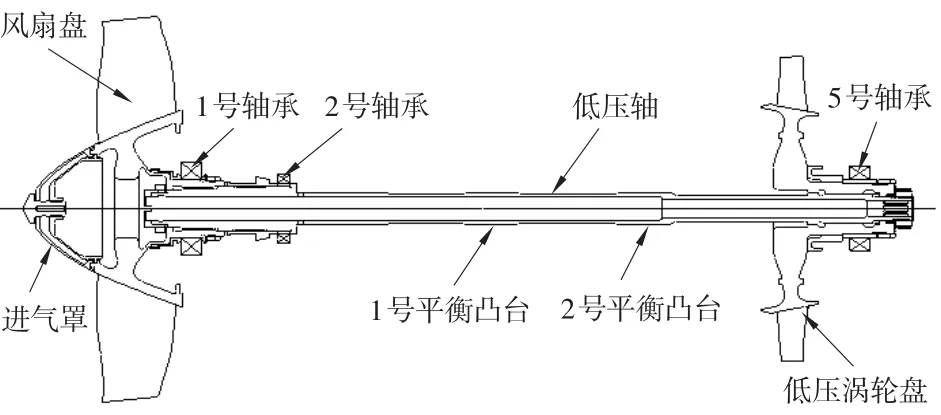
图1 低压转子结构示意图Fig.1 Structure sketch of the low pressure rotor

3 有限元计算模型

用有限元方法建立低压转子的计算模型。建模时，对转子结构进行了简化，忽略了倒角、小孔等一些细小的局部结构。计算模型如图2所示，有3个轴承单元(模拟支承)、2个集中质量单元(风扇叶片和低压涡轮叶片作为集中质量处理)、41个刚性连接单元和1 392个梁单元。

图2 低压转子的有限元计算模型Fig.2 Finite element calculation model of the low pressure rotor

4 基准支承刚度下的临界转速及其裕度和振型

4.1 临界转速及其裕度

低压转子在工程设计阶段，通过动力特性计算、分析，确定了3个支承刚度基准值，分别为1.2×107N/m、2.5×107N/m、0.6×107N/m。在该组合支承刚度条件下，计算的前三阶临界转速及其裕度见表1。表中：临界转速裕度=(|慢车或额定工作转速-临界转速|)/慢车或额定工作转速×100%；低于慢车转速的第一阶临界转速对慢车转速进行评定，介于慢车和额定工作转速之间的第二阶临界转速分别对慢车和额定工作转速进行评定，高于额定工作转速的第三阶临界转速对额定工作转速进行评定。从表中可知：低压转子超二阶临界转速工作，前三阶临界转速相对慢车转速和/或额定工作转速的裕度均大于20%，满足设计准则要求[11]，临界转速设计合理。

表1 临界转速及其裕度计算结果Table 1 Calculation results of critical speed and margin

4.2 振型

低压转子的前三阶振型计算结果见图3。从图中可知，低压转子的前三阶振型均为弯曲振型。主要是因为低压轴是一个大长径比的细长空心轴，横向刚度较低，很容易发生弯曲变形。

5 临界转速随支承刚度的变化规律

在不改变质量分布和转子结构的前提下，以4.1节中的支承刚度基准值为基准，分别改变3个支承刚度，计算转子的前三阶临界转速，以揭示低压转子前三阶临界转速随支承刚度的变化规律。

图3 低压转子的前三阶振型Fig.3 First three stage vibration modes of the low-pressure rotor

5.1 临界转速随1号支承刚度的变化规律

仅改变1号支承刚度(变化范围为0.4×107～2.0×107N/m)时，计算得到的低压转子前三阶临界转速随1号支承刚度的变化曲线见图4，前三阶临界转速的变化率见表2。可见：改变1号支承刚度，可有效调节第二阶临界转速，对第一阶临界转速也有一定的调节效果，但对第三阶临界转速几乎没有调节效果。

图4 前三阶临界转速随1号支承刚度的变化曲线Fig.4 Curves of first three stage critical speed with No.1 supporting stiffness

5.2 临界转速随2号支承刚度的变化规律

仅改变2号支承刚度(变化范围为0.5×107～4.5×107N/m)时，计算得到的低压转子前三阶临界转速随2号支承刚度的变化曲线见图5，前三阶临界转速的变化率见表3。可见：2号支承刚度在0.5×107～2.5×107N/m范围内变化时，可有效调节第三阶临界转速，对第一阶临界转速也有一定的调节效果，但对第二阶临界转速几乎没有调节效果；2号支承刚度在2.5×107～4.5×107N/m范围内变化时，对第一阶和第二阶临界转速几乎没有调节效果，仅对第三阶临界转速有一定的调节效果。

表2 前三阶临界转速的变化率(改变1号支承刚度)Table 2 Change rate of first three stage critical speed(change No.1 supporting stiffness)

图5 前三阶临界转速随2号支承刚度的变化曲线Fig.5 Curves of first three stage critical speed with No.2 supporting stiffness

5.3 临界转速随5号支承刚度的变化规律

仅改变5号支承刚度(变化范围为0.2×107～1.0×107N/m)时，计算得到的低压转子前三阶临界转速随5号支承刚度的变化曲线见图6，前三阶临界转速的变化率见表4。可见：改变5号支承刚度，对第一阶临界转速有显著的调节效果，但对第二阶和第三阶临界转速的调节效果很小。

6 临界转速随悬臂长度的变化规律

图6 前三阶临界转速随5号支承刚度的变化曲线Fig.6 Curves of first three stage critical speed with No.5 supporting stiffness

表4 前三阶临界转速的变化率(改变5号支承刚度)Table 4 Change rate of first three stage critical speed(change No.5 supporting stiffness)

为得到悬臂长度(仅增大悬臂长度，原设计的悬臂长度基本没有减小空间)对转子临界转速的影响，对转子的前三阶临界转速随悬臂长度的变化规律进行了研究。计算得到的低压转子前三阶临界转速随悬臂长度的变化曲线见图7，前三阶临界转速的变化率见表5。可见：第一阶和第二阶临界转速随悬臂长度的增大而减小，第三阶临界转速几乎不变；增大悬臂长度，对第一阶临界转速有显著的调节效果。当悬臂长度增大范围为0～80 mm时可有效调节第二阶临界转速，继续增大时调节效果非常有限。其中悬臂长度增大40 mm时，第二阶临界转速与第一阶临界转速之差最小，即第一阶临界转速与第二阶临界转速之间的稳定转速区最小，缩小或增大悬臂长度，稳定转速区均逐渐变大。

图7 前三阶临界转速随悬臂长度的变化曲线Fig.7 Curves of first three stage critical speed with cantilever length

表5 前三阶临界转速的变化率Table 5 Change rate of first three stage critical speed

7 结论

建立了低压转子的有限元计算模型，计算了基准支承刚度条件下的前三阶临界转速和振型；在不同支承刚度和不同悬臂长度条件下对低压转子的前三阶临界转速进行了系统的计算分析，揭示了低压转子前三阶临界转速随支承刚度和悬臂长度的变化规律。主要结论如下：

(1)低压转子在额定工作转速范围内存在二阶临界转速，各阶临界转速对慢车转速和工作转速裕度均大于20%，临界转速设计合理。

(2)低压转子的前三阶振型均为弯曲振型。

(3)改变1号支承刚度，可有效调节第二阶临界转速，对第一阶临界转速也有一定的调节效果；改变2号支承刚度，可有效调节第三阶临界转速，对第一阶临界转速也有一定的调节效果；改变5号支承刚度，可有效调节第一阶临界转速。

(4)第一阶和第二阶临界转速随着悬臂长度的增大而减小。增大悬臂长度，对第一阶临界转速有显著的调节效果。当悬臂长度增大范围为0～80 mm时，可有效调节第二阶临界转速，继续增大时调节效果有限。

(5)悬臂长度增大40 mm时，第二阶临界转速与第一阶临界转速之差最小，即第一阶临界转速与第二阶临界转速之间的稳定转速区最小，缩小或增大悬臂长度，稳定转速区均逐渐变大。