一种采用遗传算法优化离心叶轮结构的方法
陈鼎欣,银越千,邬国凡
(中国航发湖南动力机械研究所,湖南 株洲 412002)
1 引言
随着高功重比航空发动机的发展,以牺牲发动机油耗、机动等特性为代价,单纯通过增加结构材料提高关键零部件强度和可靠性,已难以满足先进发动机的研制需要。离心叶轮作为大多数中小型航空发动机的核心转子件,其结构性能的优劣直接影响整个航空发动机的功能实现[1]。如何通过多目标优化的方法改善离心叶轮的结构性能,提高结构质量的利用率,成为许多专家学者关注的课题[2-9]。蔡显新等[2]运用改进的耦合分析数学模型对叶轮应力分布进行了优化,陆山等[3]通过二维、三维方法对整体叶片盘进行了以改善应力分布为目的的分步优化,雒婧等[4]通过对离心叶轮叶轮背结构特征参数进行优化减小了离心叶轮的应力集中程度。然而,由于传统多目标优化的局限性,这些研究往往集中于局部特征优化,难以实现结构的全面最优设计。
遗传算法基于生物进化原理搜索最优解,在整个解群体中不断自适应地进行随机搜索,具有内在的隐并行性和更好的全局寻优能力,引入遗传算法一定程度上能克服单纯利用数值计算处理多目标优化问题的局限。刘小民等[5]运用遗传算法对离心叶轮叶片结构进行了优化设计,张明辉等[6]运用神经网络与遗传算法对离心叶轮全局优化进行了部分理论研究。不过在全面考虑设计参数特点的基础上,综合采用数值拟合与遗传算法对离心叶轮结构参数进行全局优化的相关研究还较少。
本文以结构质量与结构应力指标为优化目标,提出一种基于代理模型-遗传算法的离心叶轮结构设计参数全面优化方法。主要包括利用拉丁超立方试验设计方法获取样本数据,运用Kriging近似模型构造覆盖整个设计参数范围的响应面,以遗传算法对多目标参数响应面的高适应度区域寻优;采用整体到局部的多目标优化步骤,实现结构的优化设计;通过不同状态离心叶轮结构强度的对比分析,验证结构优化设计的有效性。
2 结构优化方法
对于离心叶轮结构优化问题,若确定结构质量最小作为主要目标,对于其他如应力、变形等目标函数只要满足一定限制条件,即可把这些函数当作约束来处理[10],从而将多目标优化问题表示为如下数学模型:

式中:X为设计变量,离心叶轮质量m为目标函数,Xs、Xt分别为设计变量的上、下限,vi(X)为约束函数。
为获取离心叶轮结构的全局优化结果,采用代理模型-遗传算法进行多目标优化。代理模型的确定包括获取试验设计样本和以样本数据为前提的数值模型替代[11]。通过合理选择代理模型构造响应面不仅能减小问题的非线性,也能有效减少对真实问题再现的计算量,提高遗传算法的效率。代理模型-遗传算法结构参数优化流程如图1所示,具体过程如下:
(1)根据待优化离心叶轮的结构特点设计初步结构优化方案,确定作为设计变量的输入参数,以及作为目标函数的输出参数。
(2)运用试验设计方法与强度计算模块,获得设计变量与响应的样本数据集合。
(3)通过样本数据点构造代理模型的响应面,并对响应面进行遗传算法寻优,形成基于代理模型的预测最优解F1。
(4)将预测最优解点的设计参数代入进行强度计算,获得目标实际解F2。由于代理模型是通过真实数据构造,故可认为遗传算法寻优的响应面是真实情况的函数替代。公式(1)通过相对误差E判断优化解是否可信。若不可信,说明构造的响应面与真实情况存在过大误差,需提高响应面精度;预测可信,即可认为对真实情况进行了有效替代,代理模型-遗传算法优化结果有效。


图1 结构优化流程Fig.1 Structure optimization process
3 离心叶轮结构优化
待优化离心叶轮为某型离心叶轮的方案设计结构,其材料为锻件TC11钛合金(强度性能见表1)。以轮盘最高工作温度260℃为屈服强度评价温度,插值获得其屈服强度为768.5 MPa。设计转速为49 000 r/min。离心叶轮前端施加78 400 N预紧力,后端面施加轴向和周向的位移约束。由于气动力对轮盘强度的影响相对较小,故文中不予考虑。轮盘强度评价采用EGD-3的标准[12],即最大当量应力σmax不大于屈服极限σ0.2,最大径向应力σrmax不大于80%的屈服极限,最大周向应力σθmax不大于95%的屈服极限。

表1 TC11性能参数Table 1 TC11 performance parameters
3.1 结构方案初步设计
离心叶轮结构初步优化方案轮廓及具体待优化参数如图2所示,初步优化参数的确定充分参考了以往设计经验并结合了其轮盘结构具体特点。
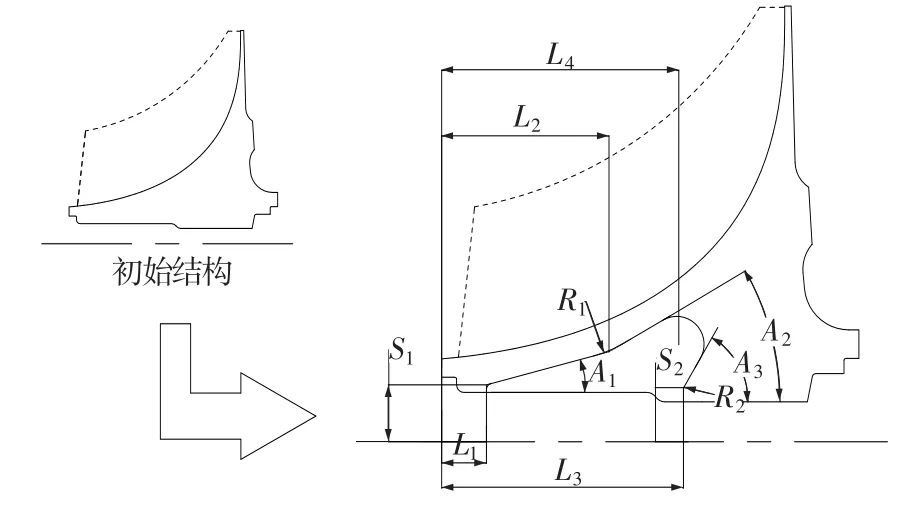
图2 参数化优化结构Fig.2 Parameterized optimization structure
运用ANSYS对初始模型及初步优化的参数模型进行稳态热力学与结构力学联合计算,并由此构造输入设计变量运行计算、提取结构质量与最大应力值为输出参数的强度计算模块。由图3中的当量应力分布可看出,初始结构的当量应力最大值在轮心边缘位置,初步优化结构的最大当量应力接近盘心中部,虽然其值有一定增加,但较大应力分布区更大,且其最大径向和周向应力均有一定程度减小。表2给出了最大应力及质量对比。由以上结果可知,本文提出的结构初步优化方案较合理,能有效优化离心叶轮的应力分布,并减小结构质量。初步优化方案的最大应力均有较大裕度,故可在强度限制条件下对结构参数进行多目标优化,以实现离心叶轮结构的全局最优设计。
3.2 结构参数整体优化
根据离心叶轮初步优化方案,选取整体多目标各参数。

图3 初始结构与初步优化结构应力Fig.3 Structural stress of initial structure and initial optimization

表2 初步计算结果对比Table 2 Comparison of preliminary calculation results
目标约束:σmax≤768.5 MPa,σrmax≤614.5 MPa,σθmax≤730.1MPa。
目标函数:m最小。
设计变量寻优范围充分考虑了去料最大化与优化结构合理性。由于拉丁超立方设计在样本空间取值的均匀分散性、取值分布随机性及充分覆盖设计空间的全面性,适合多参数、大采样空间取样[11],因此文中选择拉丁超立方试验设计获取设计变量范围内的全局样本数据。
按图1流程,通过试验设计选取90组参数样本并调用强度计算模块获得每组样本的质量与目标应力,运用代理模型构造样本数据的响应面。因Kriging代理模型具有相对更好的拟合平滑性和统计学的方差最小特征,以及对高维度问题更好的适应性[11],故文中选择该模型对样本数据进行拟合。
通过遗传算法内部寻优机制捕捉响应最优点,形成与预测点对应的强度模块提取结果的对比条件判断。式(1)中遗传算法预测可信条件取e=1%,不可信则返回计算数据加入样本数据集以提高最优区域响应面精度,可信即取强度计算结果为最终优化目标结果。
图4为相对误差随迭代次数的变化。由图可知,影响优化结果收敛的主要原因是最大径向与周向应力的预测误差,可能是由于这两项应力指标在结构优化过程中存在位置转换导致。经28次迭代,遗传算法预测结果满足收敛条件,获得的优化参数结果见表3;判断优化解收敛时,最优解下的遗传算法预测结果与强度计算结果对比见表4。

图4 相对误差的变化趋势Fig.4 Relative deviation trend
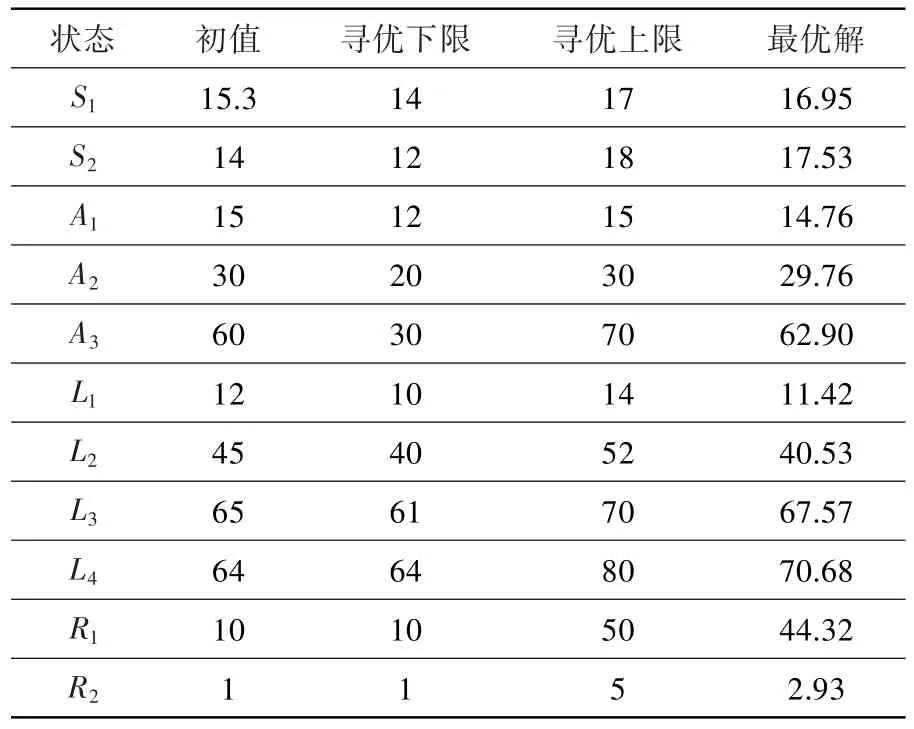
表3 设计变量优化的取值Table 3 Optimization value of design variable
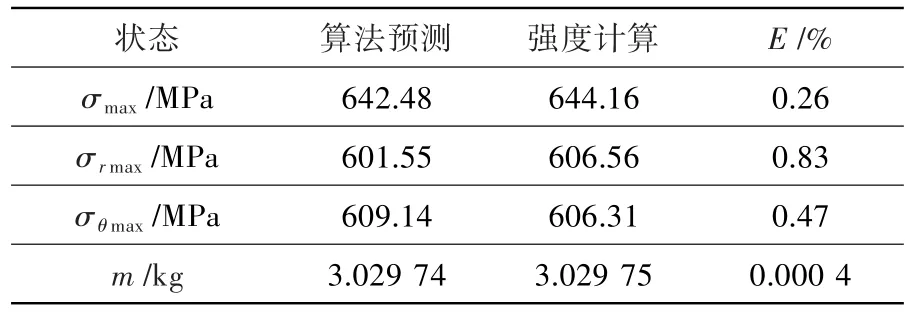
表4 整体优化结果对比Table 4 Comparison of the overall optimization results
对比表4与表2结果可知,通过代理模型-遗传算法优化,离心叶轮质量明显减小,相对于初步优化结构,整体优化后离心叶轮总质量减小约6.3%,结构的最大径向和周向应力值有一定增加,但均控制在强度约束条件内。
3.3 局部结构再优化
以整体优化后的结构参数为设计变量,将参数偏移±5%作为变量约束,通过取样和拟合,可获得在以上求得的最优解区域基于Kriging代理模型的目标函数对各设计变量的局部灵敏度,如图5所示。局部灵敏度反映了引起响应变化的输入变量的权重,正、负值分别表示正、负相关。可见,经整体优化后仍然存在局部参数对目标值影响较大的情况,故有必要选取局部灵敏度相对较高的 A3、L3、L4为设计变量,其余参数均取已求得的优化值,再次运用图1所示流程进行结构局部优化。

图5 整体优化最优解点的局部灵敏度Fig.5 The local sensitivity of optimal solution point in overall optimization
局部优化范围及结果见表5,最优点对应的优化目标函数预测及计算值见表6。对比可知,经局部参数优化,当量应力小幅增加,结构质量在整体优化基础上减小了近2.0%。可见,合理选择局部优化参数有效实现了结构再优化。

表5 局部变量优化的取值Table 5 Optimization value of local variable
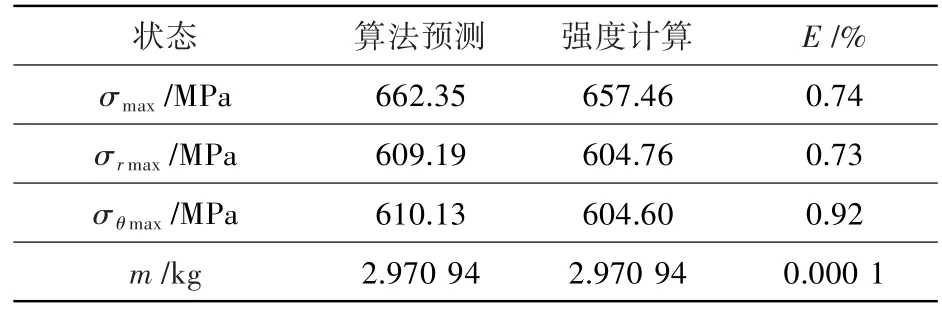
表6 局部优化结果对比Table 6 Comparison of local optimization results
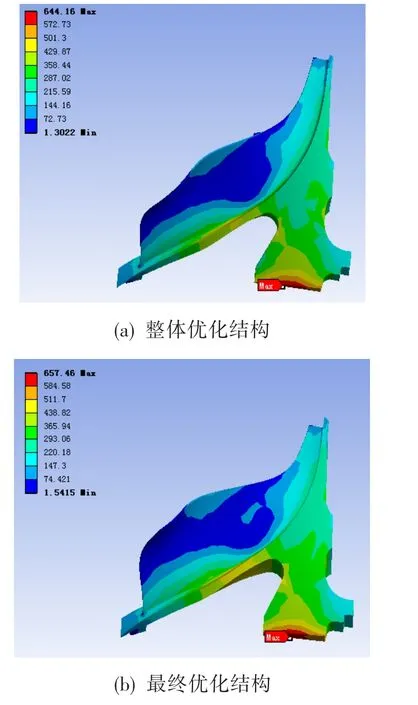
图6 离心叶轮优化结构当量应力分布Fig.6 Centrifugal impeller equivalent stress distribution
离心叶轮优化后的当量应力分布如图6所示。可见,相对于初步优化结构和整体优化结构,最终优化进一步提高了原低应力区域的应力水平,有效改善了离心叶轮应力分布不均。各阶段优化结构外形对比如图7所示。
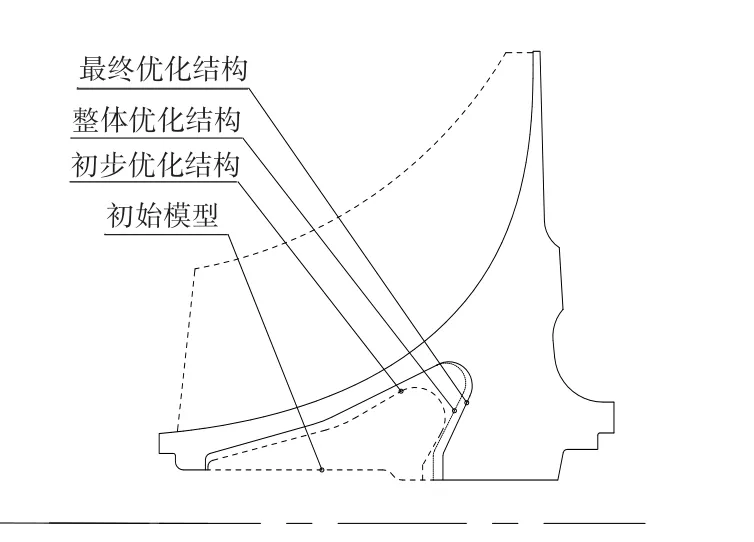
图7 优化前后结构对比Fig.7 The structure comparison before and after optimization
3.4 优化结果评价
引入平均应力值来衡量结构对质量的利用程度:

式中:σi、mi分别为不同节点位置的应力和质量。
由式(2)计算可得,初始结构、初步优化结构、整体优化结构、最终优化结构的平均应力值,分别为156.43、171.95、184.22、191.63 MPa,可见优化结构的平均承力明显提高。图8为四种结构不同应力范围的质量分数对比,可见结构优化减少了结构在200 MPa以下低应力区的质量分数,提高了高应力区质量分数。遗传算法优化显著提高了300 MPa至500 MPa质量分数,由初步优化结构的7.2%,增加到整体优化及最终优化结构的12.9%与15.4%。由此可知结构优化通过增加较大应力区比例,提高了结构的利用效率,其中通过整体-局部优化流程的提高效果更为显著。

图8 不同应力范围的质量分数Fig.8 Mass fraction of different stress ranges
另选取对压气机性能和结构布局影响较大的大叶片叶尖变形作为评价依据,根据结构优化前后其叶尖变形的变化量衡量其结构优化的可靠程度[8]。引入平均变形量:

式中:Di为叶尖某节点变形量,n为叶尖提取线上总节点数。
叶尖平均变形量Davg越小,叶片工作状态与设计状态差异越小,越有利于气动状态的稳定及气动效率的提高。图9为叶尖的总变形量的轴向分布(以顺气流方向为正)。由叶尖变形变化的趋势分析可知,结构优化后叶尖总的变形量在流道进口区域得到显著控制,初步优化结构、整体优化结构和最终优化结构最大相对减小,分别约为23.3%、46.6%和61.3%;流道中部区域变形量随优化的进行有一定增大,至叶尖出口区域又趋于一致,结构优化对叶尖出口变形影响不明显。通过式(3)进一步求得初始结构、初步优化结构、整体优化结构及最终优化结构的平均变形量,分别为0.44、0.40、0.37、0.36 mm,可见结构优化有效减小了离心叶轮叶片变形的程度。因此,在控制叶尖间隙确保安全的前提下,结构优化尤其是代理模型-遗传算法优化同时也有助于减小离心叶轮叶尖平均变形量,一定程度上提高离心叶轮整体的可靠性。

图9 叶尖总变形对比Fig.9 Comparison of the total blade tip deformation
4 结论
(1)在减重设计中对离心叶轮进行结构优化,不仅能有效减轻轮盘质量,也能使轮盘应力分布得到优化。
(2)运用代理模型-遗传算法对轮盘结构参数进行多目标分步优化,能有效提高离心叶轮结构的利用率。针对本文算例,整体优化结构相对初步优化结构总质量减小约6.3%,局部优化在此基础上还可再减小约2.0%。
(3)通过代理模型-遗传算法结构优化,离心叶轮叶尖的区域变形量得到有效控制,有助于离心叶轮整体可靠性的提高。

