均分等效面设计法的建立及其用于三组分混合物等效面的构建
葛会林,陶珊珊,朱祥伟,袁宏球,#,吕岱竹
1. 中国热带农业科学院分析测试中心 海南省热带果蔬产品质量安全重点实验室,海口 571101 2. 华中农业大学 植物科学技术学院,武汉 430070 3. 青岛农业大学 资源与环境学院,青岛 266109
大量事实表明人类和所有其他生命体在环境中都暴露于多个组分的化学混合物中。环境中污染物的混合物对生物的毒性表现为联合毒性[1]。人类在农业生产中也有目的地利用这种联合效应,常将2种、3种或更多种不同农药制剂(包括助剂)配制成混合物施用。如溴氰菊脂与敌敌畏混用防治棉蚜,氯氰菊酯与灭多威混用防治棉铃虫[2],多菌灵、腐霉利与嘧菌酯混配的杀菌剂防治铁皮石斛植物病害[3]等。农药混用可以提高药效、减缓病虫害对药剂的抗性,在化学防治有害生物方面具有重要的作用。
对于农药混用、复合污染等情况中混合物导致的加和、协同与拮抗效应的毒性相互作用,通常基于浓度加和(concentration addition, CA)作为加和性参考模型进行评估[4]。CA模型目前已成为混合物毒性预测与评估的金标准[5]。CA模型在笛卡尔坐标空间可表示为图形,对于二元混合物是直线形式的等效线,对于三元混合物则是平面三角形形式的等效面。等效线和等效面表示的优势在于可对不同浓度比例混合物的毒性相互作用进行综合图形展示。效应面在混合物中一般有2种表现形式,一种是在二元混合物中各点效应不相等的面[6],另一种是在三元混合物中各点效应相等的面[7]。
为了使观测点在图形空间均匀全面分布,需要使用优化试验设计配制混合物。直接均分射线法(EquRay)[8]和中心复合设计法[9]证明是高效的设计二元组分浓度配比的方法,可系统设计数个混合物点以全面表征二元混合物体系的浓度分布进而全面考察二元混合物的毒性变化规律,方法简单直观。对于三元混合物,目前试验次数最少的方法是采用均匀设计方法,如刘雪等[10]应用均匀设计法构建了5个不同浓度配比的混合物射线,分别研究了3种除草剂及3种杀虫剂构成的三元混合物体系的三维等效面。均匀设计被证明是在化学物混配设计中最有效的方法[11-12],其突出优点是试验次数很少、普适性好,能用于三元、六元甚至十元以上混合物的设计[13]。但对于三元混合物,均匀设计的缺点是缺少像直接均分射线法那样直观的空间几何意义。受直接均分射线法对二元组分等效线进行均匀分割设计的启发,本研究拟提出均分等效面设计(EESD)方法对三元组分等效面进行均匀分割,实现三元组分浓度配比的优化设计,同时显现其对等效面的空间几何意义。
化学物毒性检测一般使用酶、细菌、细胞、藻类、鱼等来表征污染物的毒性。酶抑制法相比生物检测具有操作简单、重复性好、测试时间短等优点。乙酰胆碱酯酶(AChE)最常用于酶抑制法当中,其基本原理是AChE催化底物乙酰胆碱(ATCh)水解得到胆碱,胆碱与显色剂二硫代二硝基苯甲酸(DTNB)反应,生成黄色物质5-硫代-2-硝基-苯甲酸,通过在412 nm检测此黄色物质的吸光度变化来反映酶催化反应的变化[14]。有机磷或氨基甲酸酯类农药对AChE有抑制作用,两者反应生成共价结合的磷酰化胆碱酯酶或可水解的氨基甲酰化胆碱酯酶。离子液体(IL)因其低挥发性可望作为挥发性有机溶剂的替代品,文献报道IL对生物也能导致毒性[15],包括对AChE也有抑制作用[16]。
本研究选择有机磷敌敌畏、氨基甲酸酯灭多威、离子液体1-丁基-3-甲基咪唑四氟硼酸盐([BMIM]BF4)作为代表化学物,使用建立的EESD方法配制三元混合物,测定混合物对AChE的抑制毒性,建立混合物观测的等效面,通过比较观测与CA预测的等效面分析混合物毒性相互作用,最终验证EESD方法的实用性与有效性。
1 材料与方法 (Materials and methods)
1.1 仪器与试剂
Synergy2型多功能微孔板测定仪(美国BioTek公司),AL204型四位电子天平(梅特勒-托利多公司),雷磁PHS-3E型pH计(上海精密科学仪器有限公司),96孔透明微板(Corning 9018)。
碘化硫代乙酰胆碱(ATCI)、DTNB与电鳗AChE等3种物质相关的具体信息见表1。DTNB、ATCI和AChE溶解于pH 6.8的磷酸盐缓冲液(含0.025 mol·L-1KH2PO4与0.025 mol·L-1Na2HPO4·12H2O)并避光保存于4 ℃冰箱中。为溶解DTNB,参考文献[14],每克DTNB中添加0.379 g的NaHCO3。受试化合物[BMIM]BF4、灭多威(MTM)与敌敌畏(DDVP)分别溶解于pH 6.8的磷酸盐缓冲液并避光保存于4 ℃冰箱中。

表1 实验中化学物质的相关信息Table 1 Information about chemicals used in the experiment
注:乙酰胆碱酯酶(电鳗)分子结构彩图来源于网址www.rcsb.org/3d-view/1C2O/1。
Note: The molecular structure of acetylcholinesterase (Electrophoruselectricus) was from the website www.rcsb.org/3d-view/1C2O/1.

表2 单个物质及三元(G0~G9)与二元(B1~B15)混合物抑制乙酰胆碱酯酶的剂量-效应模型及相关参数Table 2 Dose-response model of single substances and ternary (G0-G9) and binary (B1-B15) mixtures inhibiting acetylcholinesterase and related parameters
注:pi是混合物中组分的浓度分数;TU是以EC50计的毒性单位;c0是储备液浓度;a是位置参数;b是斜率参数;R2是决定系数;RMSE是均方根误差;EC80、EC50、EC20分别是产生80%、50%、20%效应时的浓度;c0、EC80、EC50、EC20的单位均为mol·L-1;pi与TU比中的整数0表示对应化合物不存在。
Note:piis concentration proportion of components in mixtures; TU is the toxic unit by EC50; c0is stock concentration;ais location parameter;bis slope parameter;R2is coefficient of determination; RMSE is root mean square error; EC80, EC50, and EC20are the 80%, 50%, 20%-effect concentration, respectively; all the units ofc0, EC80, EC50, and EC20are mol·L-1; Integer 0 inpiand TU ratio means that the corresponding component does not exist.
1.2 均分等效面设计与等效面构建
对于三元混合物,本研究提出EESD法进行混合配比。如图1所示,在组分a、b、c的浓度轴上点出3个组分的EC50,A点坐标为(EC50,a,0,0),B点坐标为(0,EC50,b,0),C点坐标为(0,0,EC50,c),这3点两两连接构成CA等效面,每两点所连直线为CA等效线。将3条等效线均分为3段,各均分点坐标分别为D(2EC50,a/3,EC50,b/3,0)、E(EC50,a/3,2EC50,b/3,0)、F(0,2EC50,b/3,EC50,c/3)、H(0,EC50,b/3,2EC50,c/3)、I(EC50,a/3,0,2EC50,c/3)、J(2EC50,a/3,0,EC50,c/3)。从D、E、F、H、I、J点分别作对面2条等效线的平行线,从而将等效面均分为9个全等三角形。
这9个小三角形的重心坐标分别为G1(EC50,a/9,EC50,b/9,7EC50,c/9)、G2(4EC50,a/9,EC50,b/9,4EC50,c/9)、G3(2EC50,a/9,2EC50,b/9,5EC50,c/9)、G4(EC50,a/9,4EC50,b/9,4EC50,c/9)、G5(7EC50,a/9,EC50,b/9,EC50,c/9)、G6(5EC50,a/9,2EC50,b/9,2EC50,c/9)、G7(4EC50,a/9,4EC50,b/9,EC50,c/9)、G8(2EC50,a/9,5EC50,b/9,2EC50,c/9)、G9(EC50,a/9,7EC50,b/9,EC50,c/9)。将这9个小三角形的重心坐标对应于3个组分的9个浓度配比,设计组分毒性单位比依次为1:1:7、4:1:4、2:2:5、1:4:4、7:1:1、5:2:2、4:4:1、2:5:2、1:7:1。
另外,按照惯例设计3个组分的EC50比混合物射线,对应于等效面ABC三角形的重心G0(EC50,a/3,EC50,b/3,EC50,c/3),其毒性单位比为1:1:1,又称等毒性浓度比混合物射线。这里需要指出,三元组分在三维浓度空间中的一个点可称为混合物点,组分比例相同的点构成一条混合物射线,所有的混合物射线构成一个混合物体系[17]。
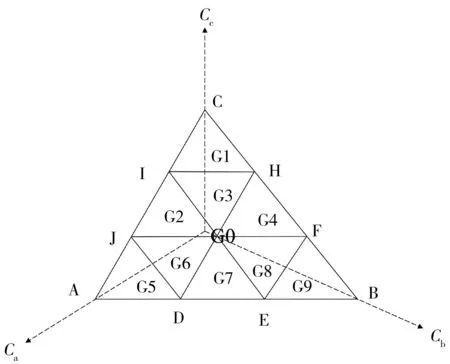
图1 均分等效面设计法设计混合物示意图Fig. 1 Ternary mixture design using equipartition equivalent-surface design method
得到混合物体系观测等效点后,采用基于三角形的三次插值得到混合物x%效应的观测等效面。基本原理是以三角形为基础的三次方程内插,即先按Delaunay三角剖分算法找出内插点四周的3个点,构成三角形,然后使用三次方程将点内插在三角形内[18-19]。具体实现这个过程的Matlab代码如下:
x=[…];
y=[…];
z=[…];
mx=min(x); %求x的最小值
Mx=max(x); %求x的最大值
my=min(y); %求y的最小值
My=max(y); %求y的最大值
Nx=50; %设置x轴插值数据点数
Ny=50; %设置y轴插值数据点数
cx=linspace(mx, Mx, Nx); %在原始x数据的最大值与最小值之间等间隔生成Nx个插值点
cy=linspace(my, My, Ny); %在原始y数据的最大值与最小值之间等间隔生成Ny个插值点
cz=griddata(x,y,z, cx, cy', 'cubic'); %调用基于三角形的三次方程进行插值
mesh(cx, cy, cz); %绘制三维网格曲面
1.3 混合物设计
基于[BMIM]BF4、灭多威与敌敌畏的储备液浓度(c0)与EC50,按照前述建立的EESD法进行三者毒性单位比1:1:7、4:1:4、2:2:5、1:4:4、7:1:1、5:2:2、4:4:1、2:5:2、1:7:1设计G1~G9共9条三元混合物射线。同时按照经典方法设置一个EC50比三元混合物射线G0。对于二元混合物,按照直接均分射线法[8]进行毒性单位比1:5、2:4、3:3、4:2、5:1两两混合设计,得到B1~B15二元混合物射线,其中B3、B8、B13为等毒性浓度比混合物射线。这些混合物射线中各组分的浓度分数见表2。
1.4 乙酰胆碱酯酶微板毒性分析
参考发光菌微板毒性分析法[20]与AChE酶抑制法[14],建立基于AChE的微板毒性分析法[21],具体分析程序如下。将96孔微板第12列的8个孔加入100 μL磷酸盐缓冲液作为空白对照,其余11列加入按稀释因子0.5设计的11个浓度梯度污染物100 μL,每个浓度8个重复,接着每孔依次加入50 μL 1 g·L-1DTNB、50 μL 1 g·L-1ATCI、50 μL 0.2 U·mL-1AChE,每孔总体积共250 μL,然后将微板送入酶标仪于412 nm下测定0 min与15 min的OD值,全程使用空调控温(29±1) ℃。
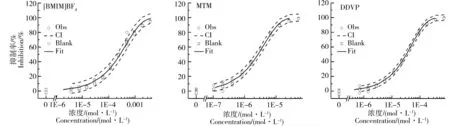
图2 单个物质抑制乙酰胆碱酯酶的剂量-效应曲线注:□空白控制;○观测数据点;—Weibull模型拟合线;┄置信区间。Fig. 2 Dose-response curves of single substances inhibiting acetylcholinesteraseNote: □ Blank control; ○ Observed data; — Weibull model fit; ┄ Confidence interval.
污染物对AChE的抑制毒性E按照公式(1)计算,得到的剂量-效应曲线(DRC)使用公式(2)所示Weibull函数进行最小二乘法拟合并计算95%的观测置信区间[22],得到效应浓度如EC80、EC50、EC20等。
E=1-△ODt/△ODc
(1)
E=1-exp(-exp(a+b×log10(C)))
(2)
式中ΔODt为处理溶液0~15 min的吸光度变化值,ΔODc为对照溶液0~15 min吸光度变化值,E为效应,C为浓度,a为位置参数,b为斜率参数。
1.5 混合物毒性预测与评估
使用公式(3)所示浓度加和(CA)模型进行混合物毒性的预测与评估。式中n是混合物的组分数,ci是产生效应x%的混合物中组分i的浓度,ECx,i是组分i单独引起x%效应时的浓度。
(3)
2 结果与讨论(Results and discussion)
2.1 单个化合物剂量-效应曲线分析
从图2可以看出,[BMIM]BF4、灭多威、敌敌畏对AChE抑制毒性的DRC呈良好的S型曲线,空白变异在测试中控制在了±10%以内。DRC经最小二乘法回归的统计参数见表2,均方根误差(RMSE)均小于0.03,决定系数(R2)均大于0.99,单个物质DRC可用Weibull函数有效表征。拟合得到的关键参数如DRC位置参数a和斜率参数b、EC80(80%效应浓度)、EC50(50%效应浓度)、EC20(20%效应浓度)同列于表2。从这3个效应浓度,都可得出对AChE抑制毒性的大小顺序为灭多威>敌敌畏>[BMIM]BF4,3种物质效应浓度的差距各接近一个数量级,单个物质EC80与EC20的差距也接近一个数量级。混合物x%效应等效面的顶点坐标分别对应单个组分的效应浓度指标ECx,ECx的精确性能保证构建的混合物体系在x%效应的CA等效面的精确性。
毒物对AChE的抑制效应主要与乙酰胆碱、毒物、AChE三者的相互作用有关。AChE的活性位点有2个结构域,即催化阴离子位点(catalytic anionic site, CAS)和外周阴离子位点(peripheral anionic site, PAS)[23]。毒物分子结构中包括芳香基团和可质子化的杂原子时,两者间满足一定的空间取向与距离要求就可以产生有效的PAS作用[24]。[BMIM]BF4含咪唑五元芳杂环,其可能与AChE活性中心带负电荷的PAS位点结合。敌敌畏是磷酸酯类有机磷农药,不同于硫代磷酯类必须经过活化作用才能发挥药效,可直接与AChE活性中心的CAS位点共价结合且抑制作用不可逆,反应速率快。灭多威是与AChE活性位点以外的部位结合且结合是可逆性的,主要是通过改变酶分子的形状来达到对AChE的抑制,为非竞争性抑制[25]。所以,[BMIM]BF4、灭多威、敌敌畏对AChE抑制具有不同的作用模式。
2.2 基于剂量-效应曲线的混合物毒性分析
图3为测得的三元混合物射线G0~G9与二元混合物射线B1~B15对AChE的DRC。结果表明,所有混合物射线的DRC都可用Weibull函数有效拟合,均方根误差(RMSE)均小于0.03,决定系数(R2)均大于0.99。拟合得到混合物的几个效应浓度EC80、EC50、EC20同列于表2。观察后发现,二元或三元混合物的EC80、EC50、EC20都分别位于单个组分EC80、EC50、EC20的最大值与最小值之间。唯一的例外是混合物B11的EC80、EC50、EC20(表2中以*标出)分别大于组分敌敌畏的EC80、EC50、EC20。我们先前的研究证明CA预测的混合物某效应浓度总是位于组分此效应浓度的最大值与最小值之间,如果混合物某效应浓度大于组分此效应浓度的最大值或小于其最小值,混合物理论上将呈现出拮抗或协同作用[26]。所以,这表明基于CA,B11在80%、50%、20%效应均产生了拮抗效应。
以观测DRC(指观测点拟合得到的DRC)的95%置信区间作为界限,CA预测效应大于置信区间上限判定混合物呈现拮抗作用,CA预测效应小于置信区间下限判定混合物呈现协同作用,CA预测效应位于置信区间上下限之间判定混合物为加和作用。另外,由于DRC拟合函数与CA模型的特性,混合物效应趋近于0%或100%时,混合物观测DRC与CA预测DRC将重合。
综合来看,G0、G2~G9、B1、B3~B5、B7~B10、B12~B15混合物射线均呈现加和作用,其中G0、G2、G3、G5、B5、B9、B10、B13混合物射线的观测DRC良好符合CA预测的DRC。剩下4条混合物射线产生了相对明显的毒性相互作用,G1在效应E<40%时为加和,在E>40%时为拮抗;B2在E<10%或E>40%为加和,在10% 图3 三元(G0~G9)与二元(B1~B15)混合物抑制乙酰胆碱酯酶的剂量-效应曲线注:□空白控制;○观测数据点;—Weibull模型拟合线;CA预测线;┄置信区间。Fig. 3 Dose-response curves of ternary (G0-G9) and binary (B1-B15) mixtures inhibiting acetylcholinesteraseNote: □ Blank control; ○ Observed data; — Weibull model fit; CA prediction; ┄ Confidence interval. 在本研究中,所有混合物效应低于10%的区域均为加和作用。这符合Escher等[27]提出的假设,即当单个化合物的浓度远低于阈值效应同时作用模式不同时,混合物将呈现加和毒性。我们先前研究的离子液体与重金属对青海弧菌Q67的联合毒性也符合这个假设[28]。 观察到一些混合物射线的CA预测DRC与观测DRC产生了相交,很明显的如B1、B2、B3混合物射线,Sun等[29]将混合物的DRC曲线穿过模型预测曲线的现象称为交叉现象,潘永正等[30]对此进行了评述,目前可以认为交叉现象在混合物中是普遍存在的,可能与混合物中复杂的联合作用模式有关。 CA理论上预测三元混合物等效面是个平面三角形,三角形顶点分别位于3个组分浓度轴上的ECx浓度点,三角形的三条边分别对应组分两两组合的二元混合物的x%效应的CA等效线。CA预测的G0~G9混合物射线的等效面与B1~B15混合物射线的等效线的具体方程见表3。CA模型是二元混合物等效线和三元混合物等效面的截距方程式表达。 绘制混合物完整的观测等效面,除了需要组分浓度轴上单个组分的3个ECx点,还需将所有三元与二元混合物的效应浓度ECx乘以各组分浓度分数后所得组分浓度在空间中对应的x%效应的等效点。这样三元混合物(G0~G9)共10个点,二元混合物(B1~B15)共15个点,3个组分共3个点。二元混合物所得点构成二元混合物等效线上的观测点,同时构成三元混合物观测等效面的三条边界。 将上述共28个等效点采用基于三角形的三次插值得到混合物x%效应的观测等效面(图4),其中分别在[BMIM]BF4与灭多威浓度轴上数据的最大值与最小值之间等间距设置50个插值点。图4中三角形为CA预测的三元混合物等效面,三角形3条边为CA预测的组分两两组合的二元混合物的等效线,等效面边界上分布的5个点对应于二元混合物的观测等效点。 CA等效面与三维坐标围成四面体,四面体内空间定义为内,四面体外空间定义为外。20%、50%、80%效应的等效面将以向外远离四面体内原点的方式依次间隔层叠。以CA等效面作为参考,观测等效面向内凹表示混合物产生协同作用,向外凸表示混合物产生拮抗作用,这个判定标准同样适合于等效面边界的观测等效线。 图4中80%与50%效应的等效面具有较为相似的特征,[BMIM]BF4-MTM基本为加和作用。随着DDVP浓度的增加,[BMIM]BF4-DDVP逐渐由加和转变为拮抗,拮抗作用最强点对应B6混合物射线DRC上的80%、50%的效应点。随着DDVP浓度的增加,MTM-DDVP逐渐从加和转变为拮抗,拮抗作用最强点对应B11混合物射线DRC上的80%与50%效应点。上述结果与基于DRC的分析也是一致的。 表3 三元混合物等效面及二元混合物等效线的CA方程Table 3 CA equations of ternary mixture equivalent-surface and binary mixture isobole 注:x是[BMIM]BF4的浓度,y是灭多威的浓度,z是敌敌畏的浓度,浓度的单位是mol·L-1。 Note:xis the concentration of [BMIM]BF4;yis the concentration of methomyl;zis the concentration of dichlorvos; the unit of concentration is mol·L-1. 图4 三元混合物在80%、50%、20%效应的等效面Fig. 4 Ternary mixture equivalent-surface at the 80%, 50%, and 20% effects 基于等效面分析,G0及G2~G9混合物射线在80%与50%效应水平均为加和作用。但G1混合物点明显外凸,故对应混合物呈现明显拮抗效应。DRC分析也表明G1混合物射线在80%与50%效应点呈现拮抗作用。同时相比G0及G2~G9混合物点,G1混合物点与拮抗作用最强的B6、B11二元混合物点距离最近,2条等效线的外凸导致G1混合物点也明显外凸,即二元混合物拮抗作用较强的区域导致邻近区域的三元混合物点也产生了拮抗作用。由于[BMIM]BF4-DDVP及MTM-DDVP等效线的外凸,加上G1混合物点向外凸,导致在[BMIM]BF4-MTM-DDVP等效面的右上侧形成了一个浅窄的鞍槽。 图4的20%效应的等效面中,二元混合物的观测等效线与CA等效线均发生了不同程度的交叉。随着DDVP浓度的增加,[BMIM]BF4-DDVP逐渐转变为拮抗,拮抗作用最强点对应B6混合物射线的20%效应点。B2混合物射线的20%效应点在[BMIM]BF4-MTM观测等效线上产生了最强的拮抗效应。MTM-DDVP基本为加和作用。G1点类似地也有轻微的外凸,但不显著。随着DDVP的浓度降低,[BMIM]BF4-DDVP与MTM-DDVP等效线逐渐内凹,导致等效面也整体以勺子状内凹,结合图3中G0~G9的DRC上20%效应点分析,三元混合物总体上呈现加和作用。 G0混合物射线DRC完美符合CA模型,反映在等效面上,G0作为其重心点,是唯一同时距离单个组分点即等效面顶点最远的点,理论上受三者彼此相互作用的影响也最小,所以最有可能表现为无毒性相互作用或加和作用。 均分等效面设计(EESD)只需知道单个化合物的EC50,不需知道其他效应浓度水平,即可进行混配优化设计。三元农药混配中比例的选择目前尚无统一的方法。如为防治铁皮石斛炭疽病,筛选含多菌灵、腐霉利、嘧菌酯的复配杀菌剂的专利配方[3]中,三药剂质量比分别为3:1:4、3:1:12、3:1:1.33、6.75:2.25:1、3:1:36、14.25:4.75:1、3:1:76 (换算后数值)。若将EESD方法应用于农药混配中,可以直接采用药剂的质量比,从而提供了一种农药混配的优化设计方法。EESD对于三元农药或三元药物的联合效应研究具有参考意义。 按照刘雪等[10]的均匀设计方案,将本研究中的[BMIM]BF4、MTM、DDVP三个组分的5个效应浓度(EC10、EC20、EC30、EC40、EC50)作为因素水平,采用U5(54)均匀表中的第1、2、3列设计了5个虚拟的混合物,基于CA模型得到这5个混合物在50%等效面上对应的点(见图5中黑点)。以最简单的四均分等效面设计作为对比,其对应的4个重心点见图5中红圈。可以看出,对于等效面,EESD点的分布更为均匀;点的覆盖范围也更大一些,这对于绘制完整的等效面是至关重要的。所以,EESD能最大程度地均匀覆盖混合物等效面,且具有明确的空间几何意义。但对于四元以上混合物,均匀设计是为数不多能用于混合物设计的方法。 试验设计是在因素可取值的区域内,最有效地采样试验点,达到采样点具有代表性以及采样点数在可接受的范围内等目的。EESD即为解决如何在等效面对应的三角形平面内高效而有代表性地采样试验点为目的。以析因试验设计作为对比,对于n个试验因素(化合物),每个因素m个水平(浓度),需安排的实验次数为mn次。如Charles等[31]应用雌激素受体试验研究3个组分的混合物毒性,其中每个化合物都以4个浓度水平进行全因子设计,需完成64次实验。Narotsky等[32]用5×5×5设计研究了乙炔化三氯、邻苯二甲酸二乙基乙酯和七氯每个化合物5个剂量水平的混合物毒性,需设计125次试验。而按照本研究中的EESD,这2个例子分别需要25次与36次试验。这里的相同点是试验次数都以指数幂形式增加,不同点是析因设计的指数为3,EESD的指数为2。 所以本质上,EESD是一种降维设计方法,将广阔的三维浓度空间压缩至二维平面进行试验设计。随着等效线分割点数增加时,如设计1、2、3、4、5个均分点时,EESD的比例总个数分别为4、9、16、25、36个,试验次数增加仍然很快,所以应根据具体的实验目的选择合适的均分数。 设组分数为n(n=3),等效线均分点数为m(m≥1且为整数),EESD法的重心坐标为(EC50,a×ea/(n×(m+1)),EC50,b×eb/(n×(m+1)),EC50,c×ec/(n×(m+1))), 其中ea、eb、ec为EESD设计的TU比中的元素。归纳后得到EESD法构造TU比的几条规则: (1)构造的比例总个数或等效面均分数目Sm,n=(m+1)^(n-1); (2)每组比例中元素均为正整数,且元素之和Se=ea+eb+ec=n×(m+1); (3)每组比例中元素e≤n×(m+1)且e≠j×n,其中j=1,…,m。 根据该规则进行排列组合可以完全唯一地构造出4、9、16、25、36均分等效面设计的比例,具体数值见表4。但该规则推广到更一般的情况还需研究与证明。 图5 均匀设计(黑点)与均分等效面设计(红圈)的三元混合物浓度点在等效面上的分布图Fig. 5 Distribution diagram of ternary mixture concentration points at the equivalent-surface based on uniform design (black dots) and equipartition equivalent-surface design (red circles) mSm,nSeEESD设计的毒性单位比例Toxic unit ratio designed by EESD1461:1:4、4:1:1、2:2:2、1:4:12991:1:7、4:1:4、2:2:5、1:4:4、7:1:1、5:2:2、4:4:1、2:5:2、1:7:1316121:1:10、4:1:7、2:2:8、1:4:7、7:1:4、5:2:5、4:4:4、2:5:5、1:7:4、10:1:1、8:2:2、7:4:1、5:5:2、4:7:1、2:8:2、1:10:1425151:1:13、4:1:10、2:2:11、1:4:10、7:1:7、5:2:8、4:4:7、2:5:8、1:7:7、10:1:4、8:2:5、7:4:4、5:5:5、4:7:4、2:8:5、1:10:4、13:1:1、11:2:2、10:4:1、8:5:2、7:7:1、5:8:2、4:10:1、2:11:2、1:13:1536181:1:16、4:1:13、2:2:14、1:4:13、7:1:10、5:2:11、4:4:10、2:5:11、1:7:10、10:1:7、8:2:8、7:4:7、5:5:8、4:7:7、2:8:8、1:10:7、13:1:4、11:2:5、10:4:4、8:5:5、7:7:4、5:8:5、4:10:4、2:11:5、1:13:4、16:1:1、14:2:2、13:4:1、11:5:2、10:7:1、8:8:2、7:10:1、5:11:2、4:13:1、2:14:2、1:16:1 注:m为等效线均分点数,Sm,n为组分数为n及等效线均分点数为m的等效面的均分数目,Se为每组比例中元素之和。 Note:mis the equipartition number of isobole;Sm,nis the equipartition number of equivalent-surface with component numbernand isobole equipartition numberm;Seis the sum of the elements in each set of ratios. 致谢:感谢中国热带农业科学院热带生物技术研究所贾瑞宗博士在文章修改中给予的帮助。感谢审稿人对提高文章质量提出的有建设性的修改意见。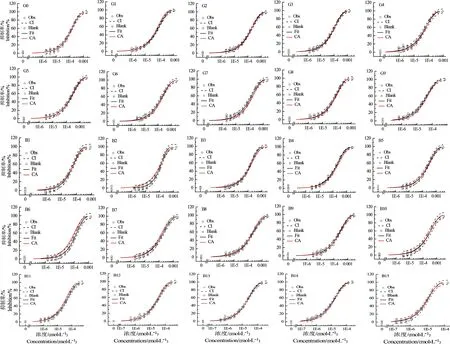
2.3 基于等效面的混合物毒性相互作用分析


2.4 均分等效面设计法拓展