基于旋量理论和代数消元6R机器人逆解算法*

赵荣波， 施智平，关 永，邵振洲，王国辉，吴立峰

(首都师范大学 信息工程学院，北京 100048)

0 引 言

机器人逆向运动学通过目标位置确定各关节角度。目前，常用的机器人运动学建模方法主要有D-H(Denavit-Hartenberg)参数法[1]和旋量法[2]。尽管在机器人运动学建模中，D-H参数法广泛使用，但当采用该方法对相邻关节平行或几乎平行的机器人进行运动学标定时，会导致参数奇异性问题[3～6]。为此，提出了许多其他运动学模型[7～9]。

为了更好地进行运动学标定，旋量指数积(product of exponentials，POE)方法广泛使用[3,6,10,11]。与D-H方法相比，其只需建立惯性和工具2个坐标系，且其运动学参数变化光滑，克服了运动学标定中存在的奇异性问题[6,10]。机器人逆运动学求解存在多种方法。Kucuk S等人[12,13]采用D-H方法分别对具有欧拉腕和偏移腕的工业机器人进行逆运动学求解。王宪等人[14]采用迭代法对6R机器人进行逆运动学求解。吕世增等人[15]将吴方法应用到机器人逆运动学的求解中。Fu Z T等人[16]应用几何代数理论对6R机器人进行运动学建模和方程求解。基于几何方法，Murray R M等人[2]介绍了3种基本子问题，且Chen I M等人[17]对子问题进行扩展，并将其应用于机器人逆运动学的求解。然而，有限的子问题不能满足所有类型机器人求解。

本文应用旋量指数积法对6R机器人进行运动学建模，采用几何、代数法和Paden-Kahan子问题并借助MATLAB处理机器人逆运动学问题，该方法为机器人逆运动学的求解提供了参考。

1 旋量理论数学基础

一般来说，刚体运动可由特殊欧氏群SE(3)中的4×4齐次变换矩阵来表示。该矩阵由3×3旋转矩阵和3×1平移位置矢量两部分组成。根据Chasles定理[2]，刚体绕某一轴的旋转和沿着该轴的平移可以完成其从某一位置到另一位置的运动，该运动称为螺旋运动，且其无穷小量为运动旋量。运动旋量的2种表示形式如下

(1)

设gst(0)为刚体相对于惯性坐标系的初始位姿，当刚体转动或平移θ后，刚体的最终位姿为gst(θ)=egst(0)。

对于只有旋转关节的机器人，当给定ξ和θ，则θ的指数形式可表示为

(2)

(3)

根据指数积公式，n自由度串联机器人末端执行器位姿可表示为

gst(θ)=ee…egst(0)

(4)

式中gst(0)和gst(θ)分别为末端执行器初始和最终位姿。

2 串联机器人逆运动学

2.1 运动学建模

机器人结构参数和旋量坐标系如图1所示。

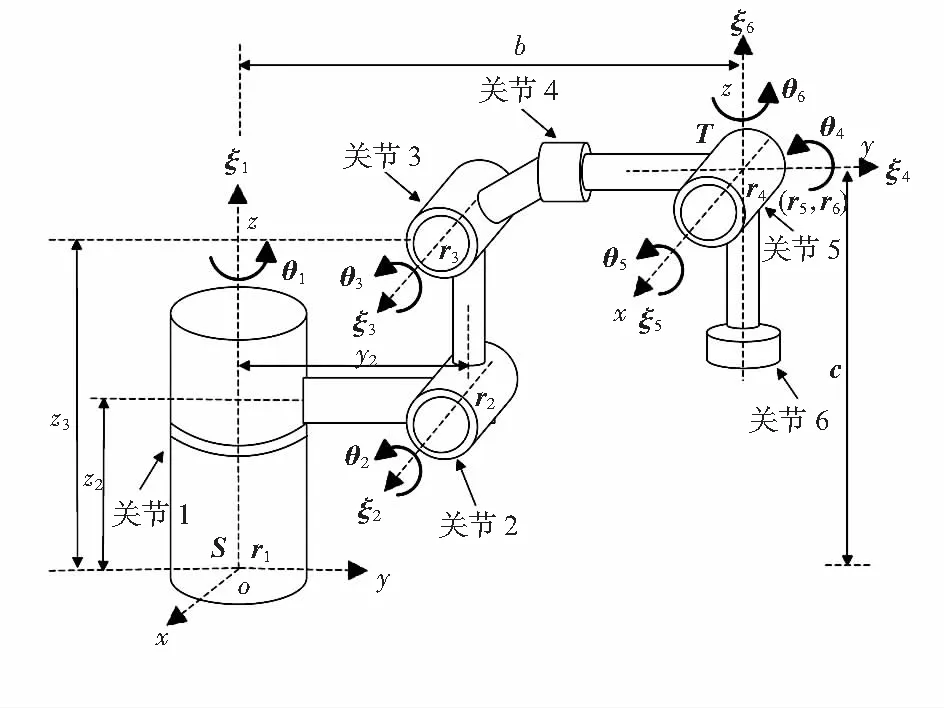
图1 机器人结构参数和旋量坐标系

可知，机器人的第2，3关节轴线是平行的，均与第1关节轴线异面垂直，且机器人后3关节轴线相交于一点，满足Piper准则具有封闭形式解。

图1中，S和T分别为惯性和工具坐标系，点o为惯性坐标系S的原点。ξ1～ξ6分别为各关节的单位运动旋量。r1～r3分别为前3关节轴线上的1点，r4～r6为后3关节轴线交点。各关节运动旋量计算为

(5)

由图1可得机器人初始位姿为

(6)

6自由度串联机器人正向运动学可由 (POE)表示为

gst(θ)=eeeeeegst(0)

(7)

2.2 逆运动学求解算法

(8)

用点r4右乘式(8)并化简得

gst1·r4=eeer4=p1=(px,py,pz,1)T

(9)

式(9)表示点r4在前3关节中的螺旋运动，其对应的2种情形如图2和图3所示。

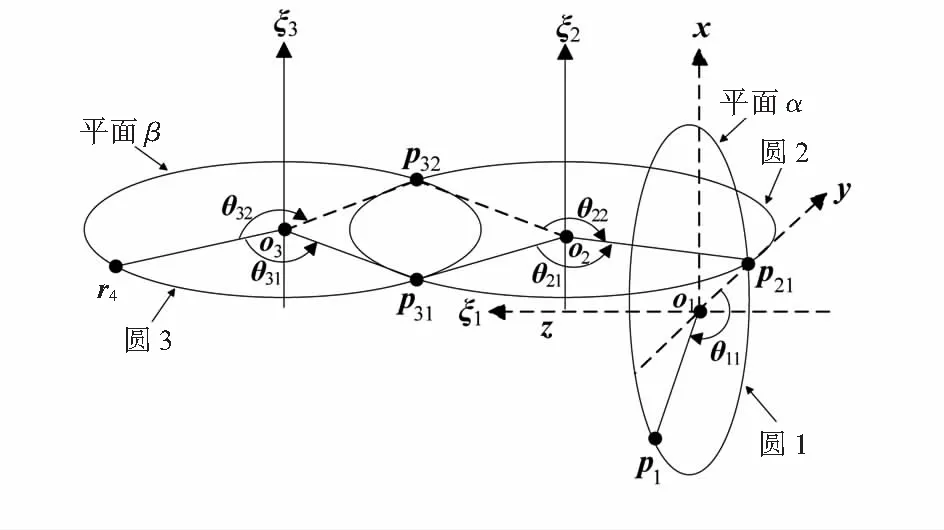
图2 前3关节螺旋运动情形一

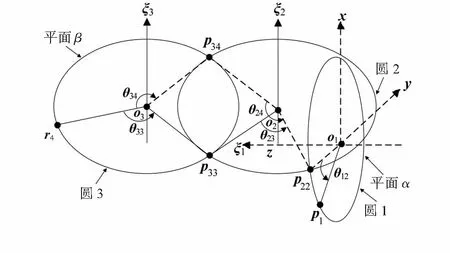
图3 前3关节螺旋运动情形二

2.2.1 求解p21和p22

在图2和图3中，点o1,o2和o3分别为圆1、圆2和圆3的圆心。p21和p22分别为圆1和圆2的2个不同交点。由机器人几何结构可知，圆1与圆2不能同时相交于2点。p31，p32，p33和p34分别为圆2和圆3的交点。图2和图3中的x，y和z轴分别对应于图1中惯性坐标系S的3个坐标轴。需要说明的是，为了便于理解，在图2和图3中将o1点与惯性坐标系的原点o重合。实际上，圆1的圆心o1不一定在o点，其可以是关节1轴线上的任意一点，但不会影响点的坐标的求解。

如图2和图3所示，在初始位姿下，首先，点r4通过绕ξ3轴旋转角度θ31(或θ32,θ33,θ34)运动到点p31(或p32,p33,p34)，然后，该点通过绕ξ2轴旋转角度θ21(或θ22,θ23,θ24)运动到点p21(或p22)。最终，该点通过绕ξ1轴旋转角度θ11(或θ12)运动到点p1。点r4和p1为已知，为了能够简单、直观地求出前三关节角度变量，则应计算出各个轨迹圆的交点。计算过程如下：

设圆1与圆3分别在平面α，β内，由于关节2和3的轴线平行，因此圆 2也在平面β内。由图2和图3可知，ξ1轴和惯性坐标系S的z轴是重合的。因o1和p1两点都在平面α内，且惯性坐标系S的z轴垂直于平面α,所以o1和p1的z坐标相等，均为pz。又因点o1为惯性坐标系S的z轴上的一点，所以o1的x，y坐标均为0。综上，o1点坐标为(0,0,pz)。

同理，因惯性坐标系S的z轴垂直于平面α，且p1,p21和p223点都在平面α内，所以p1,p21和p22点的z坐标均为pz。此外，p21和p22都在惯性坐标系S的y轴上或两点的连线平行于y轴，且均在平面β内，则该2点的x坐标都为0。因p1,p21和p223点都在圆1上，则p21和p22的y坐标分别为‖o1-p1‖和- ‖o1-p1‖。综上，可知p21和p22坐标为

(10)

2.2.2 求解p31,p32,p33和p34

由图2和图3可知，ξ2和ξ3轴线平行于惯性坐标系S的x轴，且都垂直于平面β。因点r4,p31,p32,p33,p34,o2和o3都在β内，则这些点的x坐标相同，均为0。根据机器人的特殊结构和所建惯性坐标系之间关系，可确定o2,o3坐标为

o2=[0y2z2]T,o3=[0y2z3]T

(11)

为了描述方便，用p2表示交点p21和p22，p3表示交点p31,p32,p33和p34。根据图2、图3特殊几何关系建立方程

‖o3-r4‖=‖o3-p3‖,‖o2-p2‖=‖o2-p3‖

(12)

通过求解可知，p3点坐标有4个解，因此，可以得到对应p31,p32,p33和p34坐标。

2.2.3 求解θ1,θ2和θ3

根据图2和图3，前3关节螺旋运动表示为

(13)

其由3个子问题构成，根据Paden-Kahan子问题1[2]，可得前3关节角度分别为

(14)

从图2和图3中可以看出,前3关节角度变量的解共有4种组合：(θ11,θ21,θ31)，(θ11,θ22,θ32)， (θ12,θ23,θ33)和(θ12,θ24,θ34)。

2.2.4 求解θ4,θ5和θ6

用e,e和e分别左乘式(8)，得到

eeegst1=eee=gst2

(15)

选择一点p6，使得其在ξ6轴线上但不在ξ4和ξ5轴线上，该点坐标为p6=(0,b,0,1)T。

用点p6右乘式(15)，则

gst2·p6=ee·p6=(t1,t2,t3,1)T

(16)

应用式(2)和式(3)，并借助MATLAB工具化简得

-c·sinθ4·cosθ5=t1,c·sinθ5+b=t2,

c-c·cosθ4·cosθ5=t3

(17)

采用消元法求解，可得

(18)

式中m6=-t1/cosθ5,m7=(c-t3)/cosθ5(cosθ5≠0)。

同理，用e，e分别左乘式(15)，则

ee·gst2=e=gst3

(19)

选择不在ξ6轴线上的一点p7，坐标p7=(0,b+1,0,1)T。

点p7右乘式(19)有gst3·p7=e·p7=[t4,t5,t6,1]T。

根据Paden-Kahan子问题1[2]可得θ6=atan 2(-t4,t5-b)。

至此，已得到6R串联机器人所有可能的逆运动学的解。几何方法的巧妙运用，简化了运算，加深了对多解组合的理解，有助于选择合适的逆解。

3 实例与验证

“钱江一号”[18]工业机器人满足本文所提出的机器人的结构。为了验证本文提出的逆解算法，将该机器人作为实例进行逆运动学求解。验证过程如下：

1)机器人工作空间内，任意给出6个关节角度θ1=100°,θ2=50°,θ3= -60°,θ4=180°,θ5=30°,θ6=-110°。

2)应用正向运动学方程求解机器人位姿

(20)

3)利用本文提出的算法和求出的位姿，计算各关节对应角度。共得到8组逆运动学的解，如表1所示。可以看出，第1组解与给定的6个角度完全相同。

表1 逆运动学的8组解

4)计算求出的8组逆解对应的位姿。

5)计算步骤(2)中位姿与步骤(4)中位姿差矩阵的2范数。

6)找出最大差矩阵范数及其对应的位姿误差。

通过计算，第7组逆解对应位姿差矩阵的2范数norm7为6.864 709 873 407 309×10-13为最大。

该范数对应的最大位姿误差Δgmax为

Δgmax=gst-gst7=

(21)

式中gst为步骤(2)中给定角度对应的位姿，gst7为第7组逆解对应的位姿。

4 结 论

本文提出的6R机器人逆解算法的最大位姿误差极其地小，为10-12数量级，从而验证了算法的正确性。与文献[19]相比，其最大位姿误差为10-2数量级，因此，本文提出的算法在精度方面具有很大优势。