基于ν-SVR的纸基纳米金检测Cr6+的浓度识别*

江亮亮， 罗小刚， 侯长军， 钱 烨， 霍丹群

(重庆大学 生物工程学院生物流变科学与技术教育部重点实验室，重庆 400044)

0 引 言

及时准确检测出Cr6+含量至关重要[1,2]。纳米金颗粒(gold nanoparticles,Au-NPs)因其独特的光谱特性、较高的面容比和易于表面功能化被用作一种常用的检测受体[3,4]，将Au-NPs修饰到纸基上可实现重金属离子的精确检测[5～7]。本实验室的郭建峰等人[7]采用纸基纳米金实现了Cr6+的浓度检测，具有检测限低、快速、稳定、特异性高等优点。但在基于纸基纳米金的Cr6+的检测中，如何由反应特征值自动进行浓度识别是一个亟待解决的问题。

近年来，采用人工神经网络[8]、模糊推理[9]、支持向量机[10,11]、独立分量分析和主分量分析[12,13]等智能信息处理算法进行浓度识别取得了长足进步。本文针对纸基纳米金检测Cr6+的特点，采用支持向量回归(support vector regression,SVR)实现浓度识别，并与多项式非线性回归识别和反向传播(back propagation,BP)神经网络识别效果进行对比，结果表明：基于SVR的浓度识别精度更高，能够取得更好的识别结果。

1 纸基纳米金制备

Au-NPs在较高的消光系数(108～1010(mol/L)-1cm-1)下具有很强的表面等离子共振吸收(surface plasmon resonance,SPR)效应[14]，发生肉眼可辨的颜色变化，可作为一种检测比色传感器。按文献[15]所述方式，将牛血清蛋白(bovine serum albumin,BSA)添加到纳米金溶液中，配成BSA-Au-NPs溶液。再按文献[8]所述方式制备涂有TiO2的纤维素纸基(silanization-titanium dioxide modified filter paper,STCP)，该纸基上附着巯基和氨基，确保Au-NPs颗粒不易脱落。然后将BSA-Au-NPs溶液滴加到STCP上，用去离子水清洗后烘干，制成纸基纳米金(BSA-Au-NPs/STCP)。最后将纸基放入混有HBr的待测溶液中水浴后取出烘干，采集纸基图像，实验纸基较对照纸基的颜色变化程度即可表征Cr6+的浓度。其化学变化原理如式(1)，纸基与Cr6+反应后，Au-NPs颗粒的数量和粒径减少，导致颜色变浅，颜色变化程度与Cr6+浓度呈正相关

(1)

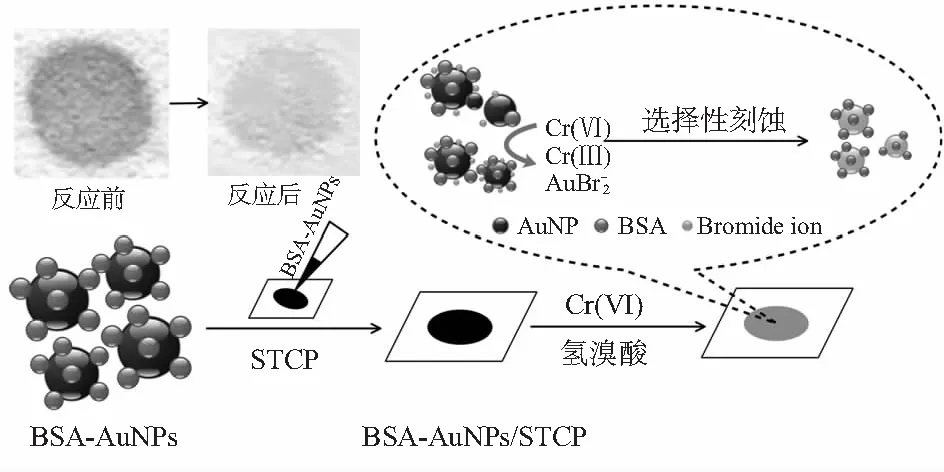
图1 纸基纳米金制备及检测

2 ν-SVR模型

SVR[10]是基于结构风险最小化和统计学习理论的机器学习方法，其具有理论严谨、全局优化、训练效率高和泛化性能好等优点。

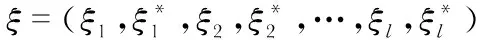
(2)

采用Lagrange乘子法对其进行优化，并引入核函数将原始样本点映射到高维特征空间，其对偶问题为

(3)

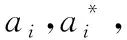
1)给定训练样本集T={(x1,y1),(x2,y2),…,(xl,yl)}∈(X,Y)，其中xi∈X=Rn,yi∈Y=R,i=1,2,…,l；

2)选择适当的参数ν,C和核函数K(xi,xj)；

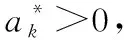
(4)

3 基于ν-SVR模型的Cr6+浓度识别

3.1 数据选取及处理

反应组纸基与对照组纸基的颜色差为分析所需的特征信息，为实现纸基纳米金检测Cr6+离子的浓度识别，选取25组实验数据，如表1所示。

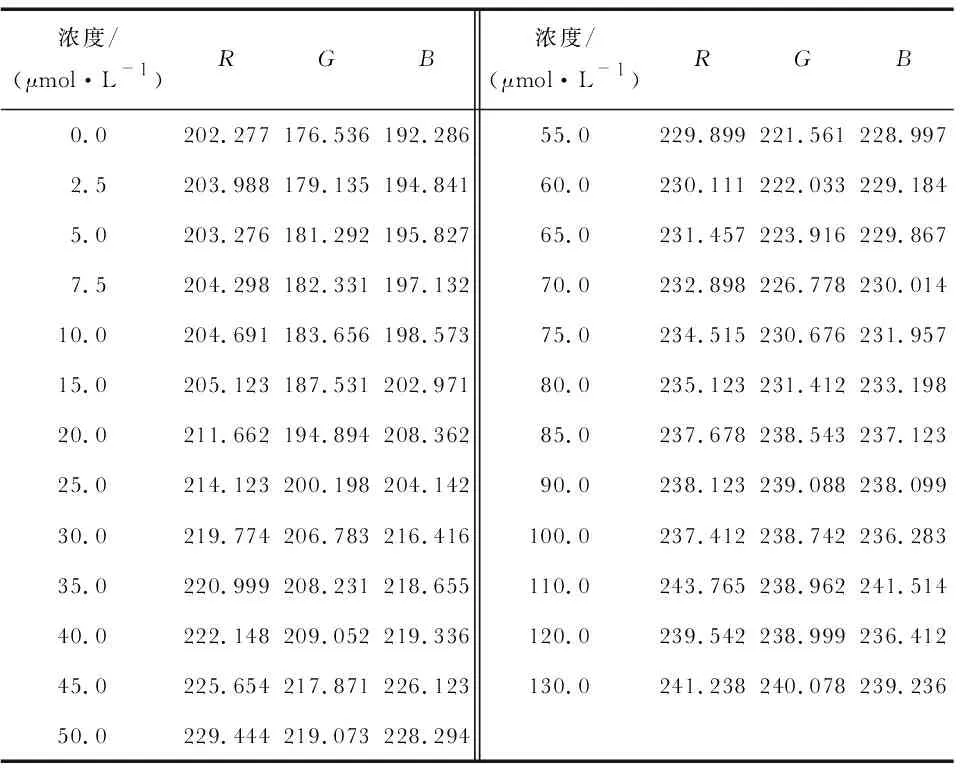
表1 纸基纳米金的Cr6+检测实验数据

各浓度纸基的颜色信息减去浓度为0时的纸基颜色信息即为颜色的变化程度，此时样本数据包含浓度、R分量变化值ΔR,G分量变化值ΔG,B分量变化值ΔB，共24组数据，n=24，其中ΔR,ΔG,ΔB为自变量，浓度为因变量。

数据归一化效果对预测结果有较大影响，选用全序列法实现数据归一化

(5)

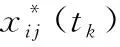
将归一化数据中的2/3作为训练集进行训练，1/3作为测试集进行验证。具体选择方式为从第3个数据开始，每间隔2个数据抽取1个数据作为测试集，余下的数据作为训练集，此时训练集共计16组数据，测试集共计8组数据。

3.2 最优参数选择

采用6—折交叉验证，在给定ε=0.001的前提下，惩罚系数C的取值范围为2-10～210，核函数参数g的取值范围为2-10～210，ν的取值范围为2-20～20，均以指数变动0.2作为步长，通过C，g，ν的不同取值，找出交叉校验误差最小时对应的那一组参数即为最优参数，RBF核函数，Sigmod核函数和多项式核函数的c,g,ν分别为85.289 3，5.076 2，0.283 1；147.199 3，0.020 6，0.856 3；50.231 2，10.442 9，0.703 2。

采用训练集以不同核函数及对应的最优参数对模型进行训练，将拟合结果分别投影到R空间、G空间和B空间进行展示。可知，RBF核的ν-SVR模型拟合的回归数据与原始数据重合率最高，拟合效果最好如图2所示。3种不同内核的模型的相关性R2分别为RBF核函数为0.997 5，Sigmod核函数为0.911 7，多项式核函数为0.969 3。

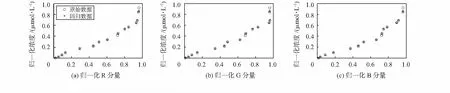
图2 RBF核函数对应的ν-SVR模型对训练集的拟合效果

可知，RBF核函数的模型拟合效果明显优于Sigmod核函数和多项式核函数，表明RBF核函数的模型其训练精度较高，训练效果较好。因此，ν-SVR模型的最优参数为：选用RBF核函数，且C=85.289 3，g=5.076 2，ν=0.283 1。以最优参数完成模型训练，即可对测试集进行预测。

3.3 识别效果评价

为验证ν-SVR模型对浓度的识别效果，采用相同的训练集和测试集，与多项式非线性回归识别方法和BP神经网络识别方法进行对比,如表2。

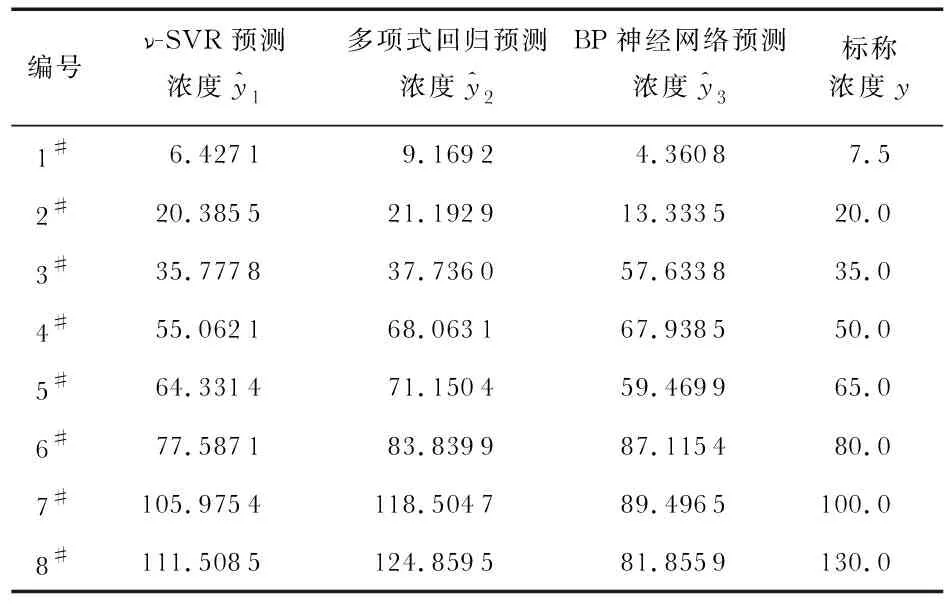
表2 测试集预测结果 μmol·L-1

平均相对误差(average relative error,ARE)表征了预测浓度与真实浓度之间的误差大小，有

(6)

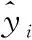
可知，ν-SVR模型对测试集的识别ARE为6.603 1 %、多项式非线性回归的识别ARE为13.608 2 %、BP神经网络的识别ARE为30.084 1 %，其中，ν-SVR模型的识别ARE最低，识别精度最高，识别效果最好。即采用ν-SVR模型可实现纸基纳米金检测Cr6+浓度的精确识别。

4 结 论

本文将SVR应用到当前的研究热点即，纸基纳米金检测中，对Cr6+浓度进行预测，根据最终的识别结果对比分析，相较多项式回归分析、BP神经网络，SVR具有更高的预测精度和较强的泛化能力，对纸基纳米金的检测研究具有重要理论价值和应用前景。