一种降低衰减直流分量影响的全波傅氏改进算法

费殷胜男， 杨向萍

(东华大学 机械工程学院，上海 201620)

0 引 言

目前，傅里叶算法广泛应用于微机继电电力保护装置中，通过提取基波分量和相角来判断故障类型。全波傅里叶算法以周期函数为模型推导，可以提取信号中的基波和各次谐波，可以完全滤除信号中的恒定直流分量和整次谐波，但在实际的故障信号中，还含有较大的衰减直流分量，传统的傅氏算法无法滤除，对于求取的基波幅值和相角精度影响很大，无法准确判断是否发生故障，危害整个电网的安全。针对衰减直流分量主要解决方向为：通过小波变换提取衰减直流分量[1，2]；通过多周期比较和多次傅氏变换来提高精度[3]；在1个周期基础上增加几个采样点求得衰减直流分量后进行滤除[4，5]；在不增加采样点的情况下进行校正等[6～10]。前两类方法计算较为复杂，不能普遍应用于嵌入式装置中；第三类算法牺牲保护装置的速动性来提升精度，在实际应用中使用较少；最后一类算法保证速动性，但是仍存在误差。

本文在已有研究基础上针对最后一类算法对含有衰减直流分量的故障波形校正：通过采样估算出衰减时间常数及衰减直流分量的初始值，由采样值减去衰减直流分量得到修正值，用修正值求得基波分量。整个计算过程可在一个工频周期内实现，误差较小且应用在微机保护装置中。

1 传统全波傅氏算法及其误差分析

以电流为例，设其故障信号为

(1)

式中I0为衰减直流分量初始值；τ为衰减时间常数；In,φn为n次谐波的幅值和初相角；ω为基频分量角频率。

根据全波傅里叶求得各谐波实部和虚部时域表达式为

(2)

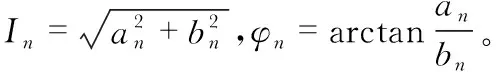
(3)

(4)

式中Ts为采样间隔，Ts=T/M。则有

=Δan+an

(5)

(6)

其中Δan，Δbn使得含有衰减直流分量的信号在进行全波傅里叶变换后存在较大误差，且无法滤除从而导致求取的幅值、相角产生偏差。因此，在采样后需要经过校正得到真实值。

2 改进全波傅氏算法

分析可知需要得到衰减直流分量的初始值I0和衰减时间常数τ才能准确地求出真实值，则令

(7)

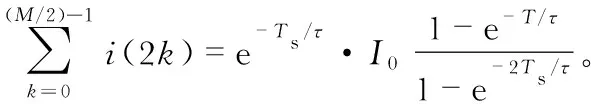
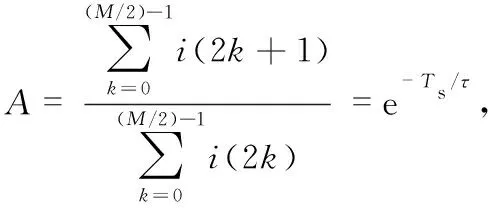
考虑到算法的应用场合，避免对数函数的出现增加嵌入式系统的运算量，因此对其进行泰勒级数展开，得到

(8)

(9)

(10)

3 仿真验证

为验证改进算法的准确性，在MATLAB上进行仿真运算[11]。设故障电流信号为

i(t)=100e+100sin(2πft)+20sin(3×2πft+π/6)+10sin(5×2πft+π/3)

(11)

式中f=50 Hz，用12 bit A/D转换器在基频周期下采样，采样点数48个，计算时取到小数点后4位。分别取τ为0.02,0.05,0.1,0.15,0.2 s,用改进算法对τ进行估算进而计算出各次波的幅值，仿真结果如表1所示。

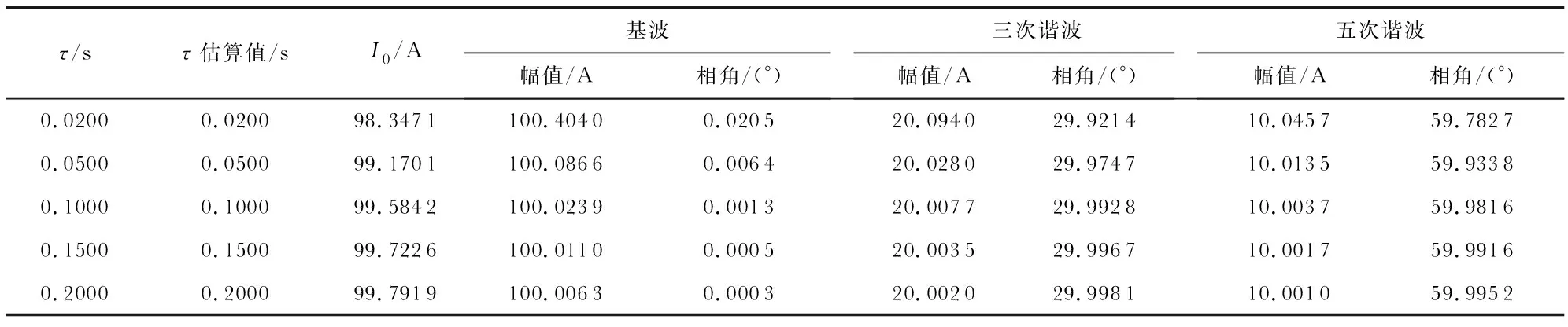
表1 仿真计算结果

算法误差主要来源为A/D采样误差、数值计算误差以及泰勒展开式取前4项引起的阶段误差。由表1分析可知，在τ的变化范围内，改进算法最大误差为2.048 %，为τ=0.02 s 求基波初相角，在误差允许范围之内，该算法对基波幅值的求取影响较小。图1为原始傅里叶算法与改进算法在τ=0.020 s时的幅值对比，传统算法最大误差达到17.26 %，而改进算法误差最大0.4 %。可以看出,改进算法准确度较高，误差较小，可有效降低衰减直流分量的影响，且计算结果较为稳定，在1个周期内即可提取基波分量。

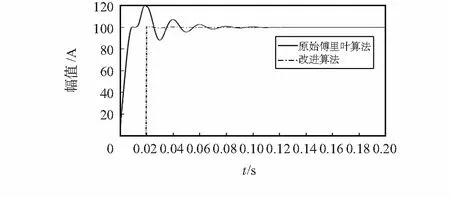
图1 传统离散傅里叶变换与改进算法比较

4 结 论

本文提出了一种可滤除衰减直流分量的算法，只需1个工频周期的采样序列即可估算出衰减时间常数以及衰减直流分量的初始值，并对序列进行补偿后进行全波傅里叶变换来提取基波分量，满足系统要求的实时性，且算法精度较高。在计算中避免指数函数和对数函数等复杂运算，通过泰勒展开式展开得到估算值，运算量小、速度快、误差较低。因此，该算法满足微机保护装置的速动性、可靠性，有利于在实际装置上的应用。