乘性噪声干扰下基于交互多模型的目标跟踪*

廖书伟， 刘 巍

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

0 引 言

随着现代航空航天技术的飞速发展，目标运动的实时性跟踪越来越受关注。对各式各样的飞行器的航速和机动性能的要求也越来越高。当目标突然实施机动(突然转弯或加、减速等)，只采用一个模型很难描述目标的运动情况[1,2]。因此，Blom和Bar-shalom在广义伪贝叶斯算法[3,4]的基础上，提出了交互多模型算法(interacting multiple model,IMM)[5,6]。交互多模型算法是目标多模型运动的常用算法之一，可尽可能真实地反映目标的实际运动情况[7,8]。然而，经典的IMM算法没有考虑受乘性噪声的影响，因此本文提出受乘性噪声干扰的IMM算法对目标运动的影响并验证。

IMM算法被广泛应用于许多不同的领域,如文献[9]运用IMM算法跟踪机动目标，研究结果表明用IMM算法跟踪机动目标模型(特别是加速度较大)有明显的优势，文献[10]研究多通道交互多模型跟踪人体运动，进一步延展了IMM算法的应用。文献[11]通过IMM算法得到其派生算法，并用于跳跃马尔可夫线性系统的风险滤波问题。文献[12]提出IMM-卡尔曼滤波(Kalman filtering,KF)算法，该算法运用于目标跟踪具有较好的跟踪精度和稳定性。文献[13]结合粒子滤波和IMM算法，应用于高速高机动目标的跟踪，提高了对非线性系统下不确定情况的滤波性能，从而也优化了跟踪精度。文献[14]结合无迹KF和IMM算法，提出了一种自适应调整“当前”统计模型的计算方法，提高了运动模式的匹配概率，改进了跟踪效果。然而，上述文献仍没有考虑乘性噪声的影响。

乘性噪声一般是由信道不理想引起的，其与信号是相乘的关系。如传输信号经过电离层信道时的衰退或反射以及信号的采样、选通、调制等[15]。文献[16,17]研究的系统中，加性测量噪声为有色噪声，所得递归滤波算法较不考虑乘性噪声有更好的性能。文献[18]研究了受有色乘性噪声干扰的线性离散系统的最优状态估计。文献[19]研究了受乘性噪声的干扰，马尔可夫参数部分未知的线性系统的状态估计问题，并验证考虑乘性噪声情况下较不考虑乘性噪声的性能提高明显。在实际应用中,因忽略乘性噪声的影响，而导致性能严重的下降。因此，研究乘性噪声干扰下的IMM算法很有必要。

在本文中，目标运动的测量方程中含有乘性噪声，通过联合使用有乘性噪声的Kalman滤波器[20]和IMM算法，得到一个针对乘性噪声环境下的IMM算法，并验证考虑乘性噪声的IMM算法优于经典的IMM算法，且能较准确地反映目标的实际运动情况。

1 乘性噪声干扰下的KF

考虑如下系统

x(k+1)=A(k)x(k)+ω(k)

(1)

(2)

式中x(k)∈Rn为未知的状态向量，ω(k)∈Rn为加性过程噪声，ζμ,k∈Rn×n为乘性噪声，y(k)∈Rp为输出向量,v(k)∈Rp为加性测量噪声,A(k),C(k),μ,k为适当维数的矩阵。

假设系统满足条件如下:

1)关于系统状态噪声ω(k)和观测噪声v(k)满足:均值都为零，方差分别为Q(k),R(k) ,且ω(k),v(k)相互独立。

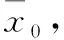
因量测值yi(i=1,2,…,k)含有乘性噪声ζμ,k,令yk[yT(0),yT(1),yT(2),…,yT(k)]T,令Y=y时X的线性最小均方误差估计与相应的最小均方误差估计相等，即[X|Y=y]=E[X|Y=y]。

a.预测估计

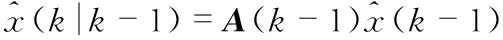
(3)

b.预测误差协方差

P(k|k-1)=A(k-1)P(k-1|k-1)AT(k-1)+

Q(k-1)

(4)

c.新息

(5)

d.卡尔曼增益

N(k)=C(k)P(k|k-1)CT(k)+R(k)+

(6)

(7)

K(k)=P(k|k-1)CT(k)×N-1(k)

(8)

e.滤波

(9)

f.滤波协方差

P(k|k-1)=(I-K(k)C(k))P(k|k-1)

(10)

将上述含有乘性噪声的卡尔曼滤波算法应用于经典的IMM算法。

2 乘性噪声干扰下的IMM算法

通过利用带有乘性噪声的KF及经典的IMM算法[6]，得到乘性噪声干扰下的IMM算法，具体如下：

1)输入交互:设模型i转移到模型j的转移概率为pij，则马尔可夫链的转移概率矩阵如下

(11)

(12)

(13)

2)乘性噪声干扰下的IMM算法

对应第j个模型，0j(k-1|k-1),P0j(k-1|k-1)以及观测值Z(k)作为输出进行卡尔曼滤波，过程如下

(14)

预测误差协方差

(15)

卡尔曼增益

Kj(k)=Pj(k|k-1)CT×[CPj(k|k-1)CT+

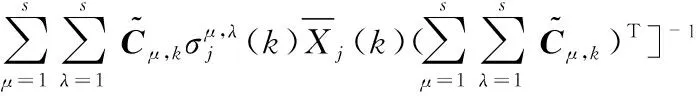
(16)

(17)

滤波

Kj(k)[y(k)-Cj(k|k-1)]

(18)

滤波协方差

Pj(k|k)=(I-Kj(k)C)Pj(k|k-1)

(19)

式中I为单位阵。

3)模型概率更新

由似然函数更新模型概率μj(k)，模型j的似然函数为

(20)

式中vj(k)=Z(k)-Cj(k|k-1),Sj(k)=CPj(k|k-1)CT=R(k)

所以,模型j的概率为

(21)

4)交互输出

总的状态估计

(22)

总的协方差估计

(23)

由于经典的IMM算法没有考虑乘性噪声的影响，当实际系统受乘性噪声干扰时，性能下降严重，且现有的基于多模型的目标跟踪的算法[4,5,21,22]很少考虑乘性噪声的影响。因此，为了提高实际系统目标跟踪的估计性能，本文提出了一个受乘性噪声干扰的IMM算法。

3 目标运动模型及仿真分析

3.1 状态方程和量测方程

设状态向量为

则状态方程为

Xk=AiXk-1+BiWk-1,i=1,2,3

(24)

目标运动的测量方程

(25)

对于上述问题，采用三个模型，第一个模型是非机动模型；第二、三模型为机动模型。控制模型的马尔可夫链的转移概率矩阵为

且各模型的概率为μ1=0.8,μ2=0.1,μ3=0.1。

3.2 恒速模型(非机动模型)

当非机动目标做匀速直线运动时，状态方程为

Xk=A1Xk-1+B1W

(26)

其中,系统的扰动噪声均为零均值、方差为Q=0.001I4×4，T=2 s为采样周期，总的采样点数为N=800/T

(27)

3.3 恒加速模型(机动模型)

Xk=A2Xk-1+B2W,

(28)

Xk=A3Xk-1+B3W

A3=

(29)

定义滤波误差的均值

(30)

定义滤波误差的标准差

(31)

式中M=50为蒙特卡洛仿真次数。

采用两点起始法，求得初始状态为

(32)

3.4 仿真分析

目标运动的真实轨迹如图1所示。图2～图4分别给出了所提出的乘性噪声干扰下的IMM算法与经典的IMM算法这两种方法的仿真比较结果。

图1 目标运动的真实轨迹

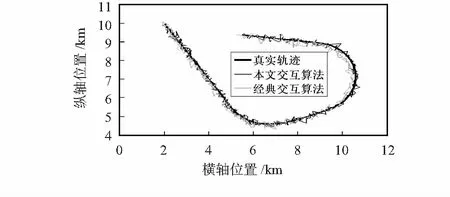
图2 目标运动的滤波轨迹

图3 x方向滤波误差的均值

图4 x方向滤波误差标准差

图2可以看出，前者滤波轨迹比后者滤波轨迹要更接近真实轨迹，且在转弯机动时使用联合乘性噪声的IMM算法比经典的IMM算法的实时跟踪更精确，效果更好。

图3、图4分别为由蒙特卡洛仿真计算得到的滤波误差均值曲线和标准差曲线，可以看出，由于有两次转弯，在转弯的前后误差的均值有较大的波动。随后在目标运动的轨迹变为匀速运动时，随着时间的推移，误差均值再次在零值附近有较小的波动。

由于x方向和y方向相同，仿真结果相类似，因此在结果分析中只分析了x方向的结果。

4 结 论

本文得到在乘性噪声环境下的IMM算法，通过对目标运动的建模及仿真分析，可以看出针对乘性噪声环境的IMM算法较经典的IMM算法能更有效地提高目标的稳定性和定位的准确性。仿真结果表明了考虑乘性噪声干扰下IMM算法的必要性。