基于改进Mahony互补滤波算法的三维运动轨迹恢复*

田红丽， 孙永全， 刘洪普,3

(1.河北工业大学 人工智能与数据科学学院，天津 300401； 2.河北省大数据计算重点实验室，天津 300401;3.华北科技学院 河北省物联网数据采集与处理工程技术研究中心, 河北 廊坊 065201)

0 引 言

长期以来，对物体运动状态的检测大多都采用外部观测的方法，即检测系统与运动物体相互分离[1]。采用外部观测方法精度固然很高，但成本相对较高，而且受制于外界条件，如全球定位系统(global positioning system,GPS)无法在室内使用，视觉传感器需要充足光线和合适角度等。近年来，随着微机电系统(micro-electro-mechanical system，MEMS)[2,3]技术的发展，体积更小、成本更低、性能卓越的新型传感器出现在大众视野之中[4]。

一直以来，基于MEMS传感器和捷联惯性导航的运动物体姿态的研究是定位导航的热点问题。文献[6～8]为基于卡尔曼滤波(Kalman filtering，KF)[9]的姿态解算过程，文献[10]将扩展卡尔曼滤波(extended Kalman filtering，EKF)[11]加入到低成本MEMS姿态解算中，但大多数研究局限于求解姿态角的范畴。2009年,刘勃等人[12]利用加速度计进行三维空间运动追踪，实验结果良好但实验较为单一。2016年,仇立杰[13]使用MEMS传感器采集数据，转换为空间数据，从而记录手势的运动轨迹，实验积分原理严谨，但呈现的空间曲线波动较大，准确性较差。

本文总结了前期算法中的精度上的不足和稳定性上的差异，参考了四轴飞行器姿态解算的方法，在原有的基础上使用四元数代替欧拉角，将Mahony互补滤波[14]算法求解姿态角的过程加以改进应用到三维运动轨迹恢复中，通过卡尔曼滤波处理加速度计带来的误差和漂移，经过积分运算，最后使用二次多项式补偿算法对速度和位移进行补偿，得出三维轨迹。

1 运动轨迹恢复

1.1 预处理

本文通过采集的三轴加速度和三轴角速度数据来进行数学运算，传感器在采集数据过程中一组或多组数据的随机误差都会对最终的积分运算结果产生影响。为了消除随机误差，采用卡尔曼滤波器对原始数据进行预处理。

设卡尔曼滤波器的离散模型为xk+1=φκxk+ωk,xk为系统状态向量，φk为系统状态转移矩阵，ωk为系统噪声。

在噪声环境下，系统测量方程为zk=Hxk+vk，vk为测量噪声，H为测量矩阵。

本文将加速度状态作为控制量加入到滤波器中有

xk+1=φκxk+ωk+BkUk,zk+1=Hxk+fφκ

(1)

式中Uk为加速度状态，Uk=[ax,ay,az]，且

(2)

1.2 积分变换原理

根据牛顿第二定律针对物体运动轨迹检测，对物体产生的加速度进行一次积分得到移动的速度，进而二次积分得到位移。由于采集的加速度数据是离散的，设传感器采样时间间隔为Δt，根据迭代的方法得出

(3)

式中v(n)为tn时刻的瞬时速度，a(n)为tn时刻的瞬时加速度，s(n)为0～tn时间段的位移。推广到三维空间，tn时刻沿加速度传感器x,y,z轴方向上的运动位移分别为

(4)

则tn时刻目标物体的空间坐标位置为(sx(n)，sy(n)，sz(n))。在三维坐标系中，连接各个时刻的空间位置坐标点即可得出空间运动轨迹。

由于物体在空间运动中会发生方向的改变，传感器所在的三轴坐标系也会随之改变，为了得出空间轨迹，需要把测得的加速度转换到恒定的参考坐标系中。设目标物体的地理坐标系为oxnynzn，传感器的载体坐标系为oxbybzb。由于矩阵方程乘法不具有交换性，从地理坐标系到载体坐标系的以Z,X,Y轴转动顺序得出的变换关系为

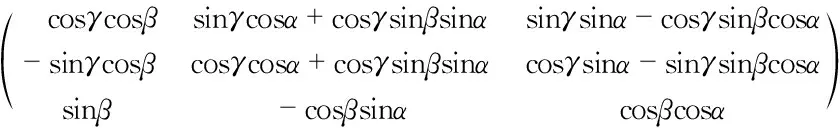
(5)

(6)

通过上式的计算，可以得到目标物体所处空间的加速度。而涉及到旋转矩阵的求解，分为欧拉角法[15,16]、方向余弦法[17]、四元数法。其中四元数法只要解四个未知量的线性微分方程即可，计算量小，易于操作，也满足实时性要求，本文采用四元数法来求解旋转矩阵。

欧拉角表示的方向余弦矩阵用四元数表示为

(7)

1.3 改进的Mahony互补滤波算法

本文将广泛应用于四轴飞行器和平衡车上的Mahony互补滤波姿态解算算法，调整后应用到三维运动轨迹恢复实验中。考虑到三轴的电子罗盘数据的误差波动，算法只保留了加速度计的数据来修正陀螺仪快速解算带来的误差。

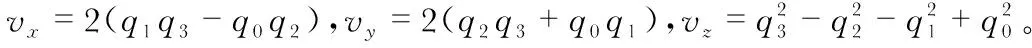
设载体坐标系上加速度计测出的重力单位向量a=(ax,ay,az)，而v为陀螺积分后的姿态推算出的重力向量，均载体坐标系上的重力向量。各量的误差向量就是陀螺积分后的姿态和加速度计测出的姿态间的误差。向量之间的误差，用叉乘来表示。叉乘的大小与陀螺积分误差成正比，可以用于纠正陀螺仪。程序上可以对e进行PI控制[18]修正陀螺仪零偏,即

E(n)=E(n-1)+Ki×e

g(n)=g(n-1)+Kp×e+E(n)

(8)

式中g=(gx,gy,gz)为陀螺仪角速度数据。 通过调整Ki和Kp两个参数能够借助加速度数据快速修正陀螺仪角速度数据。

通过求解四元数的微分方程，进行四元数的更新，其中T为测量周期，传统的求解采用一阶龙格库塔法求解,由于四元数更新是整个算法实现的关键一步，本文提出采用高精度的四阶龙格库塔法取代原有的一阶龙格库塔，使算法在四元数求解这一部分实时性准确性更佳。最终以归一化后的四元数利用式(8)计算当前的旋转矩阵，求出地理坐标系下的加速度，进行二次积分得出位移。

2 多项式位移补偿

在实际中，累积误差会导致系统的初始状态和终止状态与理论不符。为解决这个问题,文献[19]论证了使用多项式对速度和位移积分结果重建的可行性，并通过一次多项式实现了该算法。本文拓展了多项补偿理论，将系统的累积误差分配到整个计算过程。具体算法如下：

设速度补偿二次多项式为

vr(k)=v(k)+b1k2+b2k+b3

(9)

位移补偿多项式

(10)

根据理想状态下运动开始前和终止后速度为零，开始前加速度和位移也为零，即vr(0)=0,vr(ke)=0,ar(0)=0,sr(0)=0，ke为运动终止时间。速度与位移的补偿多项式为

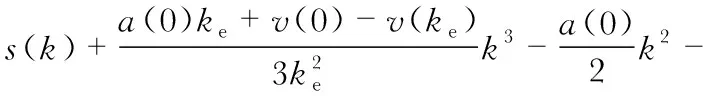
v(0)k-s(0)

(11)

3 实验与结果分析

本文的实验分为两个部分，实验一使用iPhone se手机内置的传感器，通过MATLAB MOBILE采集加速度数据和角速度数据，进行常规运动的轨迹还原实验。实验二使用MPU6050九轴运动传感器，采集数据进行进一步实验验证。

实验首先对原始加速度和角速度数据通过本文描述的卡尔曼滤波进行预处理，处理后的数据进行坐标系的旋转变换，根据积分原理得出位移再进行补偿得到轨迹。对三轴加速度数据预处理的前后对比发现本文描述的卡尔曼滤波对数据波动起到的平滑作用显著，减小了随机误差。

实验一取手机在水平方向从左侧到右侧的进行一次简单的平移。根据手机内置传感器轴向，如图1所示，轨迹应当为一条平行于x-y平面的平滑曲线。为了检测3种算法的实验效率，实验中将初始位置设为三维坐标原点，图2(a)为使用手机内置传感器对应三种算法的空间轨迹。

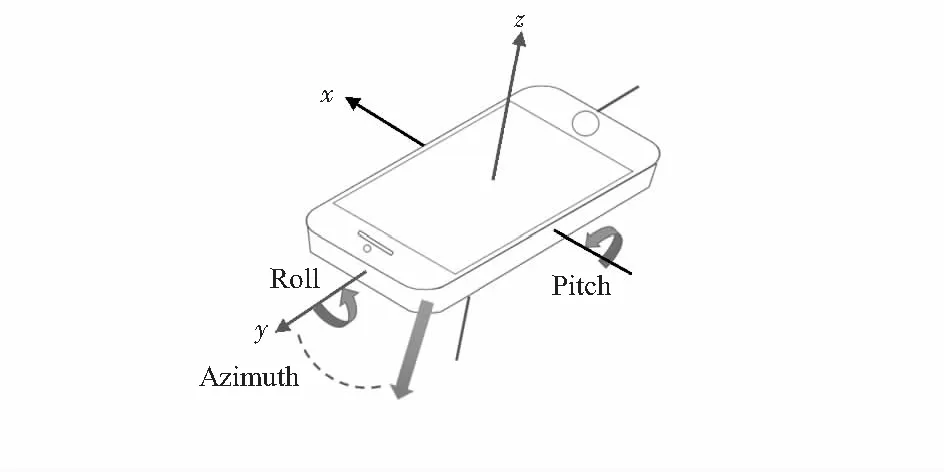
图1 手机内置传感器坐标轴方向

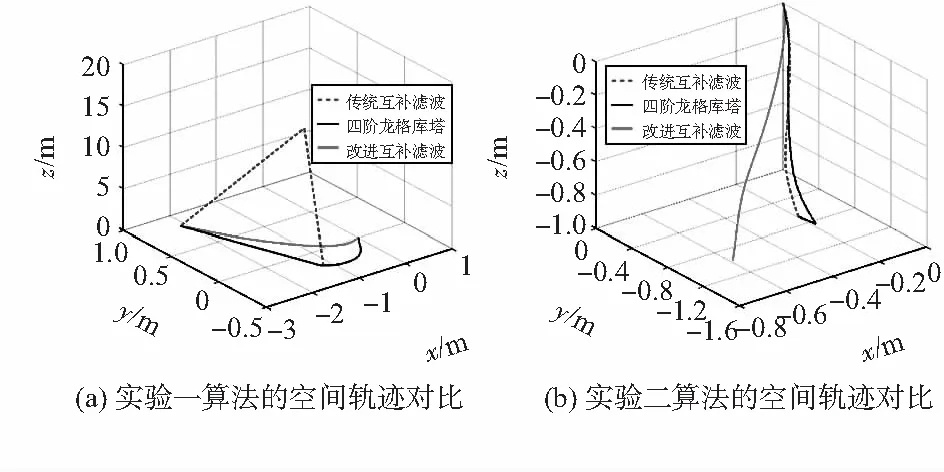
图2 实验结果

通过比较三条空间曲线，传统Mahony互补滤波算法计算的三维曲线在z轴的波动巨大，接近8 m，算法的准确度较差。使用经典四阶龙格库塔法更新四元数得出的曲线后段近似直线，z轴的波动极小，但从原点出发后的前段曲线在z轴和y轴的方向上有明显的波动，且整条曲线不够平滑，算法鲁棒性不足。改进后的Mahony互补滤波算法实现，整条轨迹相对平滑，z轴的波动范围控制在[-0.05,0]m,比较完整地复现手机运动的轨迹，改进后的算法较前两种准确性和鲁棒性明显提高。

实验二使用MPU6050九轴运动传感器在单位立方空间中从上到下做斜线运动，同时比较三种算法的轨迹。图2(b)可以看出，传统Mahony互补滤波算法和经典四阶龙格库塔法求解的轨迹在x轴方向迅速收敛，没有达到预期的位置，四阶龙格库塔法的曲线在后段有向y轴的波动，平滑度不够。改进后的互补滤波算法求解的轨迹接近预期的位置，且曲线平滑，轨迹恢复的完整度高，验证了算法的准确性和鲁棒性。

4 结束语

本文以定位和导航的理论为基础，对室内场景下运动物体的轨迹恢复进行了深入研究。将改进后的的Mahony互补滤波算法运用到实验中，使用两种传感器测出的加速度和角速度数据，经过预处理，坐标系变换，旋转矩阵更新，位移补偿进而求得运动物体的轨迹。实验结果证明：改进Mahony互补滤波算法在准确性和鲁棒性上有明显优势，在三维运动轨迹恢复的研究中有很大应用价值。