复合材料太阳帆板连接架强度的有限元分析

, , ,

(1.上海民航职业技术学院航空制造系, 上海 200232; 2.上海电机学院材料学院, 上海201306)

0 引 言

随着信息科技和航天科技的迅猛发展，卫星在人类生活中起到日益重要的作用。太阳帆板是卫星的能量来源，其复合材料连接架的强度直接影响卫星的使用寿命。在卫星发射时，太阳帆板通常处于收拢状态，待进入运行轨道后才展开[1]。太阳帆板在展开后，一般通过连接架与推进舱连接，因此对连接架的结构强度和刚度都有较高的要求。同时，为了降低连接架的质量，提高卫星的使用寿命，通常选择碳纤维复合材料作为太阳帆板连接架的首选材料[2]。虽然当航天器的大小与种类不同时，所用复合材料连接架的结构也略有不同，但连接架结构强度和刚度要求都较高。因此，在设计连接架的结构时，有必要对其结构强度和刚度进行分析，而有关复合材料连接架强度的有限元模拟的研究较少。

基于复合材料的结构特点，通常采用六面体或四面体单元对复合材料进行逐层网格划分；根据复合材料的铺层形式和铺层方向，得到各向异性材料的性能，进而计算分析单层材料的应力状态，最后再进行强度校核。然而，复合材料的层数一般较多，厚度较小，在进行网格划分时单元数量特别庞大。为此，作者采用三维等效法计算复合材料的等效刚度常数，建立复合材料太阳帆板连接架的均衡三维有限元模型，分析其应变分布情况；根据霍夫曼失效准则，得到太阳帆板连接架不同部位的强度包线，然后将强度包线与模拟所得应变进行对比，以对连接架结构强度进行校核；对复合材料太阳帆板结构进行静力试验，对有限元分析结果进行验证。

1 复合材料三维等效刚度常数

通常采用经典层压板理论对二维复合材料结构的力学性能及工程常数进行描述，但是该理论并不适用于厚板结构的复合材料。ENIE等[3]根据三维复合材料结构的特征，提出了均衡铺层复合材料结构三维弹性性能的描述方式。SUN等[4]在此基础上对该描述方式进行了完善和简化，提出了单种材料体系的三维复合材料结构性能的计算体系，并得到了广泛应用[5-7]。

复合材料层合板通常采用循环的单个子层压板进行周期性铺层，而该子层压板一般包括多个铺层角度且各向正交异性的纤维材料。在计算该复合材料层合板的三维等效力学性能时，通常先在局部坐标系中计算单向复合材料的单元柔度矩阵，在此基础上计算整体坐标系中的单元柔度矩阵，然后通过柔度矩阵结果计算得到刚度矩阵，进而计算得到复合材料结构的等效刚度矩阵，最后计算得到复合材料的三维等效刚度常数。N层各向正交异性铺层的复合材料层压板的等效弹性常数的计算公式[4]为

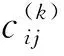
根据复合材料单层板存在弹性对称面的特性，得到其等效弹性矩阵[8]为

(15)

因此复合材料的等效柔度矩阵为

(16)

由此得到复合材料层压板的等效三维刚度常数的计算公式[6],为

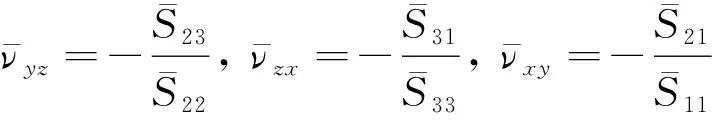
(17)

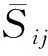
2 复合材料太阳帆板连接架的强度分析

卫星太阳帆板的典型结构如图1所示。复合材料太阳帆板连接架通常由主梁、套筒和接头构成，且这3种构件均由碳纤维复合材料制造而成。其中：接头为实心结构，通过两侧的套筒与主梁连接；主梁和连接套筒均为盒型薄壁结构，其主要作用为减轻质量并保证一定的强度。

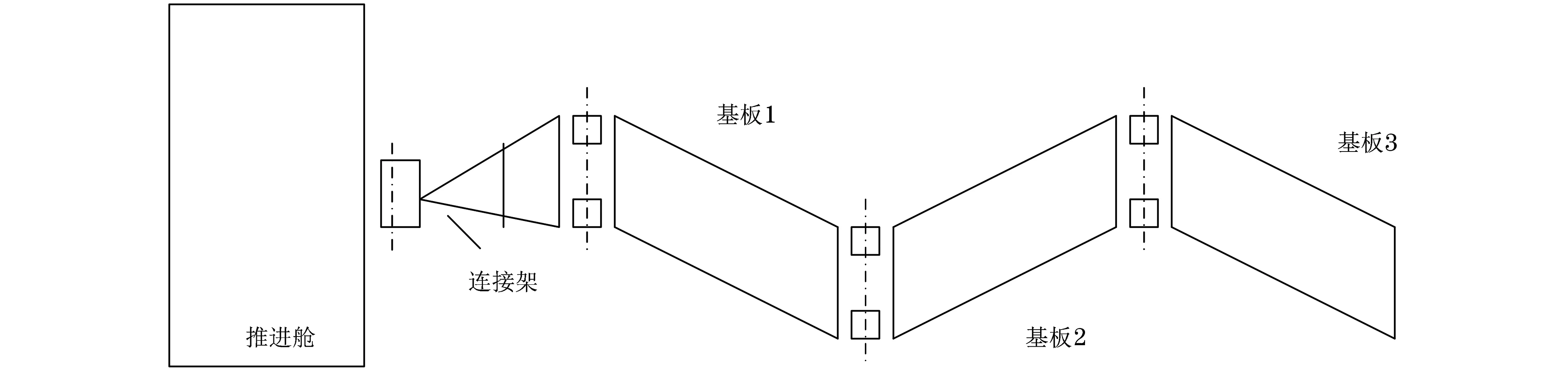
图1 卫星太阳帆板的典型结构Fig.1 Typical structure of solar array in satellite

2.1 有限元模型的建立

太阳帆板连接架的有限元模型及其分解模型如图2所示，连接螺栓采用梁单元进行网格划分，其他均采用六面体单元进行网格划分。约束载荷施加位置为主梁与接头的螺栓连接处，外加载荷施加位置为主梁端部，其中弯矩为1 835 N·m，剪力为787 N。

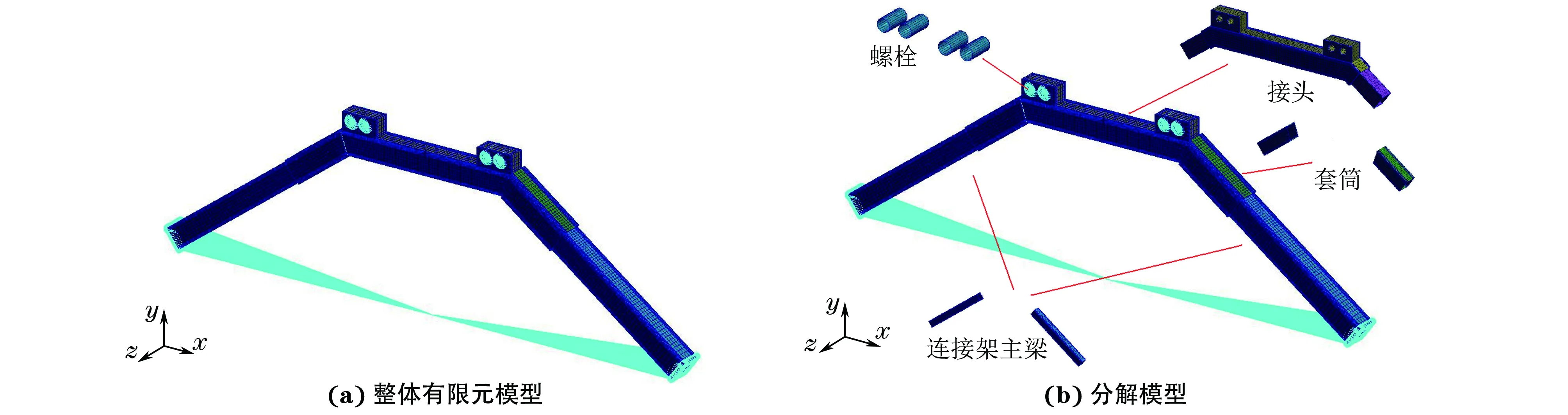
图2 太阳帆板连接架的有限元模型及其分解模型Fig.2 Finite element model (a) and its decomposition model (b) of solar array connector

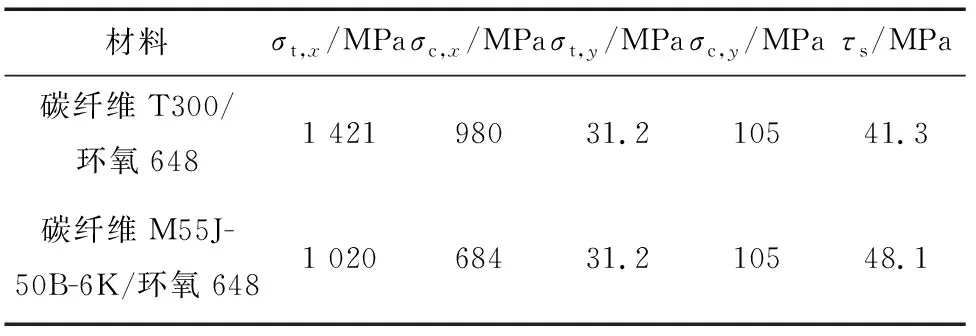
复合材料太阳帆板连接架主要采用碳纤维T300/环氧648复合材料进行铺层设计，其中：接头采用0°和90°交替正交铺层方式，单层厚度0.2 mm；接头两端根部表面至1.5 mm深度处采用0°和90°交替正交铺层方式，而芯部则采用0°单向铺层，且0°方向与主梁方向平行；连接套筒采用±45°铺层形式，单层厚度为0.2 mm，总厚度为2 mm；主梁的盒型薄壁梁分别采用碳纤维M55J-50B-6K/环氧648复合材料和碳纤维T300/环氧648复合材料进行0°和90°交替正交铺层。2种复合材料的弹性性能参数如表1所示。根据各部件的铺层形式，即可按照式(17)计算得到多层复合材料的等效弹性常数。

表1 复合材料的弹性性能参数Table 1 Elastic property parameters of composite material

2.2 强度校核结果分析

基于复合材料的等效弹性常数，采用有限元模拟得到的太阳帆板连接架不同部位的应变分布如图3～图5所示，图中的εx,εy分别为沿x,y方向的应变。由图3～图5可知，接头两端、接头底部、主梁与套筒接触位置以及套筒拐角处均存在较大的应变。

霍夫曼准则是针对复合材料的一种综合破坏准则，可同时考虑复合材料的拉压、横向以及剪切强度，并对强度之间的相互影响进行描述，适用于各向异性的多种复合材料。其极限失效判断参数R的计算公式为

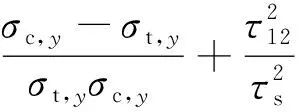
(18)

式中：σ1为沿纤维方向的应力；σ2为垂直于纤维方向的应力；τ12为剪应力；σt,x,σc,x分别为沿纤维方向的拉抻、压缩强度；σt,y,σc,y分别为垂直于纤维方向的拉伸、压缩强度；τs为面内剪切强度[9]。

当R=1时，认为复合材料层压板发生失效。

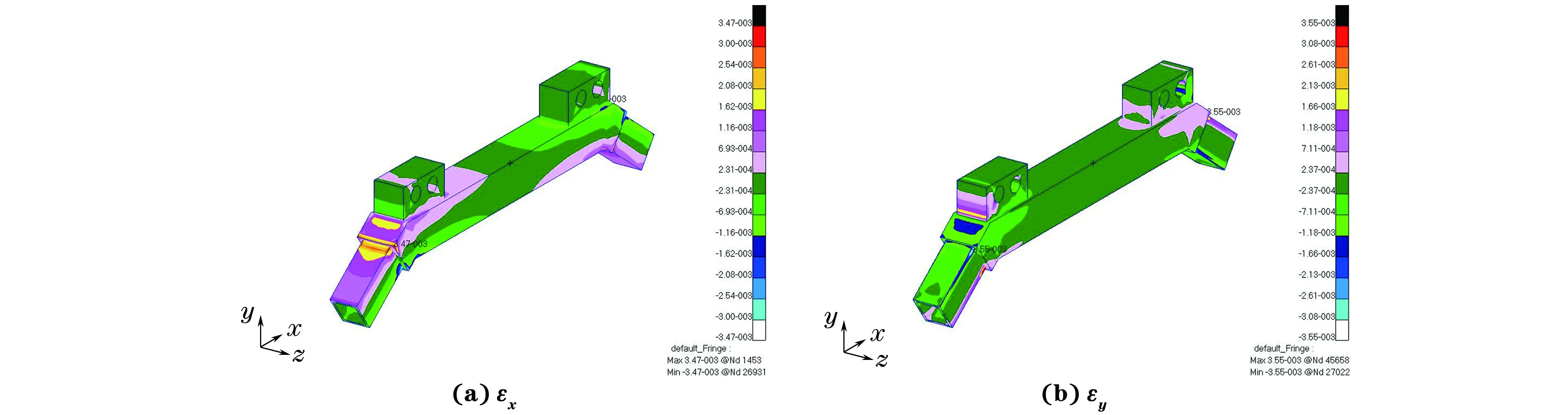
图3 连接架接头的应变分布云图Fig.3 Strain distribution contours of joint of connector

图4 连接架套筒的应变分布云图Fig.4 Strain distribution contours of sleeve of connector

在复杂载荷条件下，将霍夫曼准则作为复合材料层压板的极限失效条件，采用ESAComp3.0软件分别计算主梁层压板、接头层压板、接头端部以及套筒层压板的εx-εy曲线，绘制其强度包线，2种复合材料的强度性能如表2所示，计算结果如图6所示。

由图3～图6可以看出：连接架两端在x，y方向的最大应变分别为0.003 2，-0.003 5，处于强度包线内，可知该结构在设计载荷下不会发生失效；主梁的最大应变位于其与套筒接触位置，其x，y方向的最大应变分别为0.002 4，-0.000 6，处于强度包线内，可知该结构不会发生失效；连接套筒的最大应变位于拐角处，x，y方向的最大应变分别为0.005 0，-0.001 2，不在强度包线内，可知该结构会发生失效；连接架接头在x，y方向的最大应变分别为0.003 5，

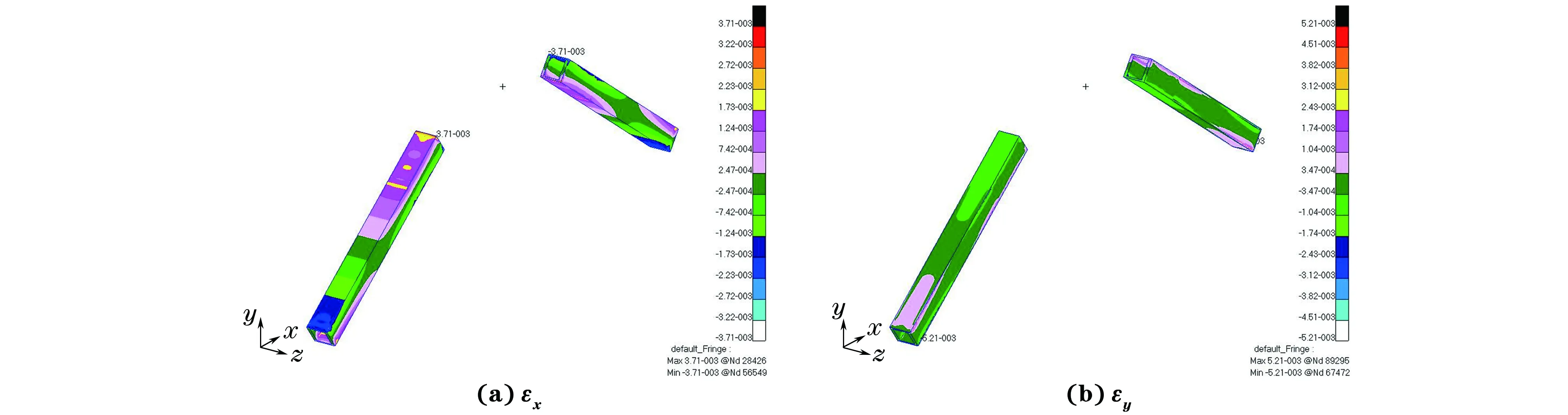
图5 连接架主梁的应变分布云图Fig.5 Strain distribution contours of main girder of connector

图6 套筒层压板、接头端部层压板、主梁层压板、主梁腹板和接头层压板的强度包线Fig.6 Strength envelope of sleeve laminates (a), connector end laminates (b), main girder laminates (c) and connector laminates (d)

材料σt,x/MPaσc,x/MPaσt,y/MPaσc,y/MPaτs/MPa碳纤维T300/环氧6481 42198031.210541.3碳纤维M55J-50B-6K/环氧6481 02068431.210548.1

-0.001 5，不在强度包线内，可知该结构会发生失效。

3 试验过程与试验验证

3.1 静力试验过程

采用上述复合材料的铺层方法，等比例制作复合材料太阳帆板连接架各组件，并进行静力试验；约束载荷施加位置为主梁与接头的螺栓连接处，外加载荷施加于主梁端部位置，大小均与有限元仿真的一致。

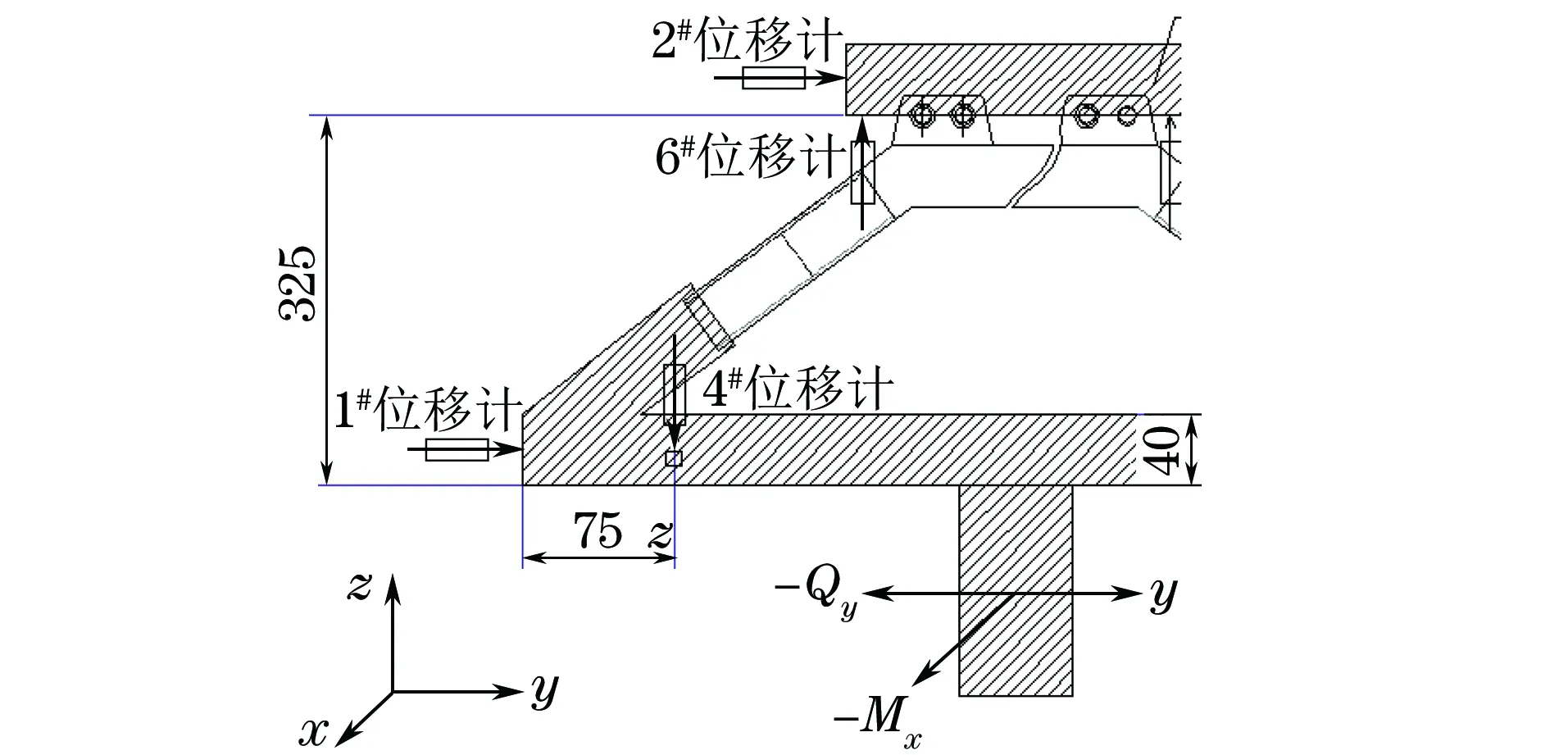
图7 静力试验装置示意Fig.7 Diagram of static testing device

静力试验装置如图7所示，采用7个位移计测加载过程中试验装置的位移，从而确保加载过程中试验装置、太阳帆板连接架以及载荷的协调性。为了测量载荷加载过程中主梁与套筒连接处的应变，在该位置布置8个双向电阻式应变片，同时测量0°和90°方向的应变，共测16个应变，应变片位置如图8所示。在加载过程中，先施加较小的预载荷，随后以设计载荷的5%进行逐级增加载荷，直至太阳帆板失效。

3.2 试验验证

由表3和表4可以看出：模拟结果与试验结果较为接近；主梁与套筒连接处0°方向应变结果的相对误差较小，最小值为0.21%，最大值为9%左右；90°方向应变结果的相对误差比0°方向的略大，最小值为0.78%，最大值为13.30%。模拟结果与试验结果存在误差的原因：试验材料的制备工艺不稳定导致材料性能与理论值存在误差；采用应变片测静力试验过程中的应变时，测量结果存在误差；有限元模型中的各向异性材料的性能是采用等效模型计算得到的，其结果存在一定误差。

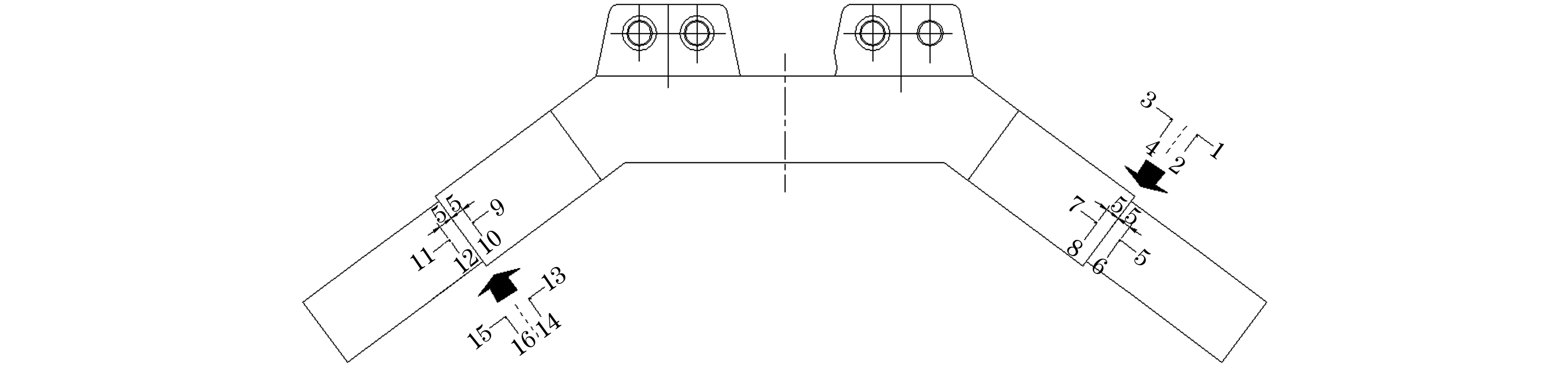
图8 应变片位置示意Fig.8 Diagram of strain gage position

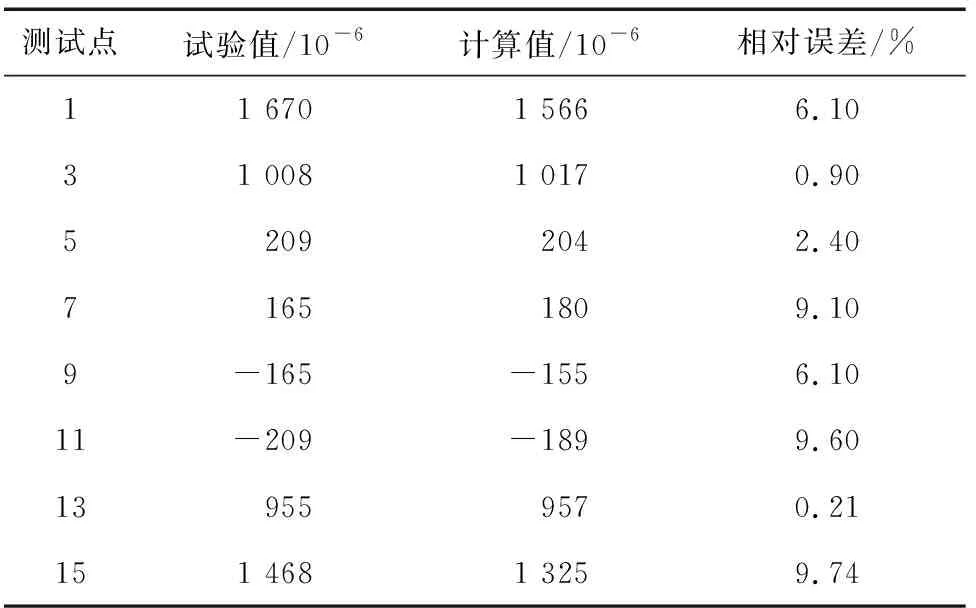
测试点试验值/10-6计算值/10-6相对误差/%11 6701 5666.1031 0081 0170.9052092042.4071651809.109-165-1556.1011-209-1899.60139559570.21151 4681 3259.74

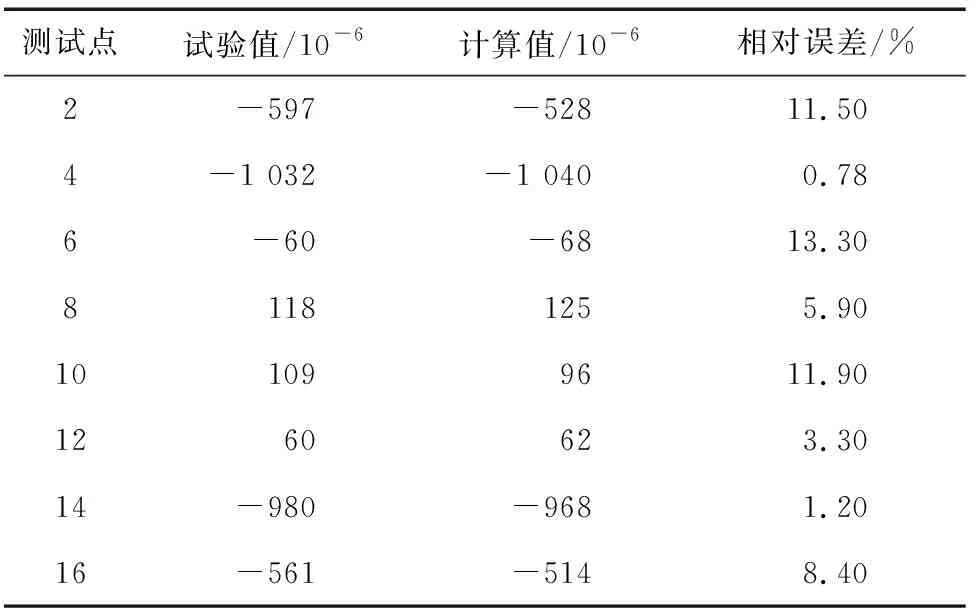
表4 主梁和套筒连接处90°方向应变计算结果与试验结果的对比Table 4 Comparison of the strain testing results in 90° directionat the joint of main girder and steel with calculation results

由图9可知：在静力试验过程中，当载荷达到设计载荷的85%时，太阳帆板连接架接头端部出现裂纹，y方向碳纤维发生断裂；当载荷增加到设计载荷的100%时，套筒拐角位置发生破坏，y方向碳纤维发生断裂。由此可知，复合材料太阳帆板连接架失效位置为接头端部和套筒拐角处，该两处位置为太阳帆板连接架的薄弱环节，这与强度校核结果一致，因此验证了该有限元模拟的准确性和有效性。

图9 静力试验过程中不同载荷下太阳帆板连接架的失效位置Fig.9 Failure positions of solar array connector under different loads during static testing: (a) load of 85% designed loads and (b) load of 100% designed loads

4 结 论

(1) 采用复合材料三维弹性等效法，建立了均衡三维有限元模型，得到太阳帆板连接架在外加载荷作用下的应变分布状态，模拟结果与试验结果较为接近；主梁与套筒连接处0°方向应变结果的相对误差较小，最小值为0.21%，最大值为9%左右；90°方向应变结果的相对误差比0°方向的略大，最小值为0.78%，最大值为13.30%。

(2) 基于霍夫曼失效准则，采用太阳帆板连接架不同部位的强度包线对连接架的结构强度进行校核，校核结果与静力试验结果相吻合；复合材料太阳帆板连接架在接头端部和套筒拐角位置均出现裂纹，这2处为太阳帆板连接架的薄弱位置。