概率安全评估和可靠性分析中故障树的重要度分析

宋述芳，马艺琰，王璐

(西北工业大学 航空学院，西安 710072)

0 引 言

故障树分析(Fault Tree Analysis，简称FTA)是复杂系统可靠性、安全性和风险评估的一种有效方法[1-2]。FTA方法是由H.A.Watson在1961年首次提出，并应用于民兵式导弹发射系统，取得了卓越的成绩。经过几十年的发展，FTA逐步形成了完整的理论，并广泛应用于核工业、航空航天、机械制造、电子电力、交通和化工等各个领域。

FTA方法是将系统故障的形成原因按照树枝状逐级细化的图形演绎方法，可以形象地反映故障发生的因果关系。通过概率安全评估的定性和定量分析，可以分析出系统的薄弱环节，指导系统的安全运行，并最终实现系统的优化设计[2]。故障树的定性分析是通过寻找最小割集，来识别所有导致系统故障的故障模式，从而发现系统的薄弱环节，判别系统的潜在故障，以便优化系统的设计，指导系统的故障诊断。故障树的定量分析是利用故障树的计算模型，在已知基本事件发生概率的条件下，求顶事件的发生概率，即失效概率，以及通过临界重要度分析来全面考虑基本事件对顶事件发生概率的影响程度。

在故障树的可靠性分析中，将故障树的基本事件的发生概率看作随机输入变量，将故障树的结构函数作为可靠性分析的状态函数，可通过数字模拟法求得系统的失效概率[3]。全局灵敏度(也称为重要测度)[4]可以全面求解基本变量对失效概率的影响，从而确定重要的基本事件，以指导系统的优化设计，具有与临界重要度相同的目的和作用。

在工程结构分析中，安全性和可靠性都是结构质量管理的重要方面。针对相同的故障树，安全概率评估和可靠性分析都可以进行结构故障的概率分析和重要度分析，那么两者分析的顶事件发生的概率以及基本事件的重要度有哪些区别和联系？由于安全性和可靠性的理论体系有差异，无法直接定量推导进行分析比较。本文通过对三个飞机系统的故障树进行概率安全评估和可靠性分析，以期得出失效概率和重要度表征的定性结论。

1 概率安全评估的故障树分析

故障树分析方法是安全系统工程中常用的一种分析方法。这种方法将系统可能发生的某种事故与导致事故发生的各种原因之间的逻辑关系用树形图的方式表示出来，通过对故障树的定性和定量分析，找出事故发生的主要原因，为确定安全对策提供可靠依据，达到预防和控制事故发生的目的。

1.1 最小割集

将同时发生就能导致顶事件发生的基本事件的组合称为割集，最小割集是能够引起顶事件发生的最低数量的基本事件的组合。最小割集指明了哪些基本事件同时发生就可以使顶事件发生的故障模式，即每个最小割集都是顶事件发生的可能途径。最小割集的数目越多，系统的危险性越大。

1.2 概率函数

故障树的概率函数是指由基本事件X1,X2,…,Xn发生的概率q1,q2,…,qn组成的顶事件发生概率的计算式g(q)。求出故障树的最小割集后，可依据其来表达故障树的概率函数。

(1) 当不同的最小割集中不包含相同基本事件时，故障树的概率函数可以写成最小割集逻辑“加”形式。

(2) 有相同的基本事件，需要使用不交化方法，利用布尔代数运算法则，使最小割集的交集变为不交集，然后按每个最小割集发生概率的代数和来计算顶事件的发生概率。

1.3 临界重要度

定义临界重要度为基本事件发生概率的相对变化率与顶事件发生概率的相对变化率的比值，反映了当基本事件发生概率变化时，对顶事件发生概率变化量的影响程度。则第i个基本事件的临界重要度系数Ic(i)[2]为

(1)

2 可靠性估计中的故障树分析

将故障树的结构函数作为可靠性分析的状态函数，将基本事件的发生概率作为随机输入变量，就可以对故障树进行可靠性分析。

2.1 失效概率

假设随机输入变量的联合概率密度分布函数为ρ(X)，用Monte Carlo法随机抽取N个样本点xj(j=1,2,…,N)，即可估计得出失效发生的概率Pf[3]为

(2)

2.2 全局灵敏度指标

可靠性分析中，局部灵敏度指标通常用失效概率对分布参数的偏导数来表达，不能考虑参数的变异性对结构响应的影响。全局考虑输入变量的不确定性对输出响应不确定性的影响程度，需要进行全局灵敏度分析。

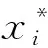
(3)

失效概率全局灵敏度指标具有如下特性：(1)ηi≥0, 如果ηi=0，则输入变量Xi对失效概率没有影响；(2)如果设置变量组，则可以考虑该变量组对失效概率的交叉影响，且ηmax=η1,2,…,n。失效概率全局灵敏度指标表征随机变量的取值规律对失效概率的影响程度，能够全面地衡量各输入变量对失效概率的贡献，为可靠性设计提供有用信息。

3 算例分析及说明

式(2)确定的失效概率与概率安全评估中顶事件发生的概率是否一致？式(1)和式(3)确定的重要度排序是否一致？它们之间是否存在一定的关系？用以下三个飞机结构的故障树为例，进行分析说明。

算例1 以某飞机襟翼失效[5]为例，将该飞机襟翼机构的单侧不对称运动失效作为传动及控制系统失效的顶事件。襟翼传动机构及控制系统运行的联接关系描述如下：内襟翼由1号和2号作动器驱动，且这两个作动器都未设置监控内襟翼倾斜角的传感器。外襟翼由3号和4号作动器驱动，这两个作动器都设置监控外襟翼倾斜角的传感器。襟翼传动机构最外侧的扭力管处装有两个位置传感器，用于监控单侧襟翼的位置。襟翼位置控制系统由1号和2号襟翼控制单元组成，该控制系统是冗余的，能够自动隔离故障控制单元的信号从而采用正常的控制装置进行控制。如果控制单元的信号显示襟翼系统是倾斜或者非对称的，那么控制驱动装置将会使襟翼停止运动并将襟翼控制在安全范围内。

飞机襟翼的单侧不对称运动故障树如图1所示。在图1中，顶事件T表示襟翼不对称运动失效事件。故障树由8个中间事件(用Mi(i=1,2,…,8)表示)、12个基本事件(用Xi(i=1,2,…,12)表示)和多个逻辑门构成。中间事件和基本事件的物理意义如表1所示[6]。

图1 单侧襟翼不对称运动模型故障树

事 件物理意义基本事件的发生概率M1可监控的襟翼不对称运动单侧传动故障且监控功能失效-M2内襟翼分传动路线故障使内襟翼发生不对称运动-M3襟翼不对称运动监控功能失效-M4可监控的单侧传动故障使襟翼不对称运动-M5总传动路线故障-M6外襟翼分传动路线故障-M7外襟翼分传动翼展方向故障-M8外襟翼分传动翼弦方向故障-X11号襟翼控制装置监控功能失效4.6×10-3X22号襟翼控制装置监控功能失效4.6×10-3X3襟翼驱动装置至1号襟翼作动器之间的扭力管组件故障4.0×10-4X4两个105°角齿轮箱中至少一个发生故障5.8×10-2X51号襟翼作动器机械故障不能带动扭力管运动4.0×10-2X61号襟翼作动器翼弦方向传动故障不能驱动内襟翼运动1.8×10-6X72号襟翼作动器翼弦方向传动故障不能驱动内襟翼运动1.8×10-6X82号襟翼作动器翼展方向传动故障不能带动外侧扭力管3.5×10-4X92号和3号襟翼作动器之间扭力管组件传动故障4.5×10-2X10161°角齿轮箱中传动故障不能带动外侧扭力管运动8.5×10-2X113号襟翼作动器翼弦方向传动故障不能驱动外襟翼运动2.5×10-6X124号襟翼作动器翼弦方向传动故障不能驱动外襟翼运动2.5×10-6

(1) 概率安全评估的分析结果

顶事件发生的概率：g(q)=8.052×10-6

临界重要度排序：Ic(1)=Ic(2)>Ic(6)=Ic(7)>Ic(10)>Ic(4)>Ic(9)>Ic(5)>Ic(3)>Ic(8)>Ic(11)=Ic(12)

通过概率安全评估的确定性分析，认为飞机襟翼单侧不对称运动故障中应重点关注1号、2号襟翼作动器翼弦方向故障(X6与X7)和1号、2号襟翼控制装置对于襟翼不对称运动的监控功能失效(X1与X2)，同时也应关注161°角齿轮箱中传动故障不能带动其外侧扭力管运动事件(X10)。

(2) 可靠性模型及分析结果

将可靠性模型的输出量假定为顶事件T发生的概率，而12个基本事件发生的概率看作模型的输入量，且用Xi(i=1,2,…,12)来表示[6]。12个输入变量均服从对数正态分布，其均值在表1最后一列给出，并假定所有输入变量的误差因子均为2。可靠性分析所得顶事件发生的概率为8.060×10-6，全局灵敏度指标确定的重要度排序为：η6η7η11η12η1η2η8η3η10η4η5η9。

概率安全评估的临界重要度和可靠性分析的全局灵敏度指标的对照如表2所示。

表2 算例1临界重要度和全局灵敏度指标的对照表

故障树顶事件发生的概率值基本一致；可靠性分析的全局灵敏度指标η所确定的基本事件的重要性排序与概率安全评估中的临界重要度的排序顺序并不一致；{X6,X7,X1,X2}依然是重要基本事件，但{X11,X12}的重要度排序发生了巨大的变化。

算例2 以波音飞机升降舵操纵分系统为例，依据其功能的示意图(如图2所示)，建立故障树。设顶事件为升降舵不能到达指定位置；构建故障树的边界条件为：不考虑安定面的影响，并且侧重于分析其机械故障[7-8]。构建的升降舵操纵系统的故障树如图3所示，其中的顶事件、中间事件及基本事件的名称说明以及基本事件发生的概率如表3所示。

(1) 概率安全评估的分析结果

顶事件发生的概率：g(q)≈2.464×10-10

临界重要度排序：Ic(1)>Ic(2)>Ic(3)>Ic(4)>Ic(9)>Ic(6)=Ic(5)>Ic(7)=Ic(10)>Ic(8)=Ic(11)

可以看出：离合器和传感器的信号传递是重要事件，要保证升降舵正常工作，首先要确保的是离合器和传感器的正常工作，而后的临界重要度排序基本是按照基本事件发生的概率大小进行排序的，即着重考虑轴承的磨损和间隙等渐变损伤造成的升降舵不能到达指定位置的失效。

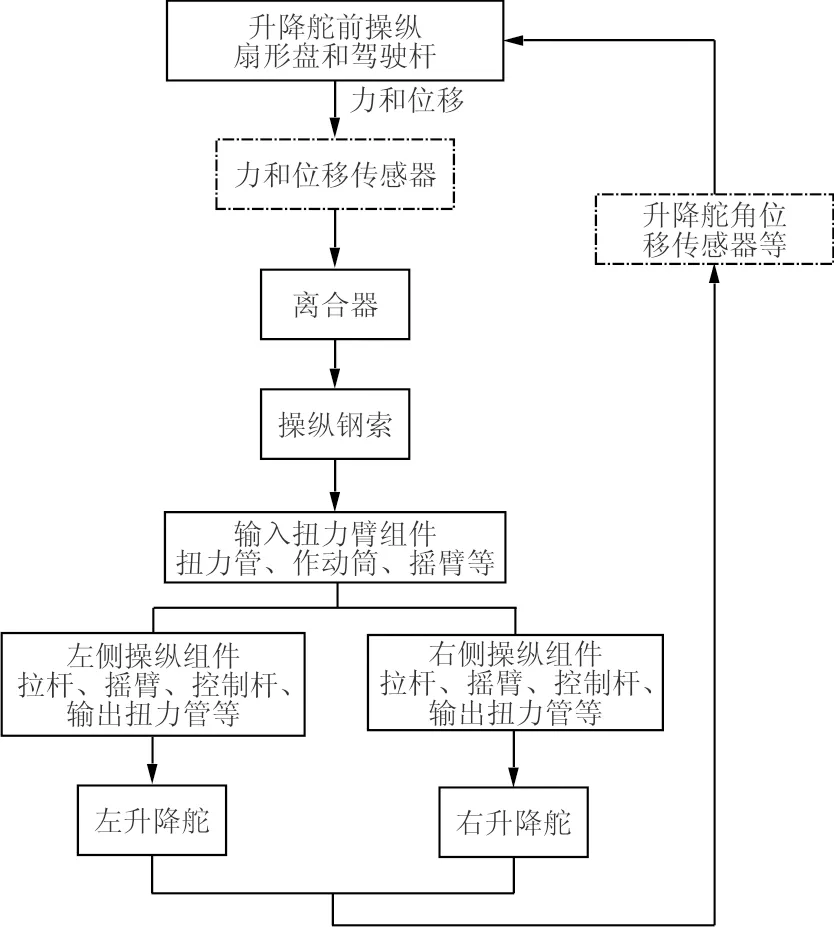
图2 波音737-NG飞机升降舵操纵系统的功能示意图

图3 波音737-NG飞机升降舵操纵系统的故障树

序号事件事件名称基本事件发生的概率1T升降舵不能到达指定位置-2M1升降舵动作量与指令不符-3M2升降舵机械卡滞无动作助力器与机械操纵卡滞,同时离合器故障-4M3升降舵轴承组件故障-5M4助力器与机械操纵卡滞-6M5左侧助力器与机械操纵卡滞-7M6右侧助力器与机械操纵卡滞-8M7左侧机械操纵卡滞-9M8右侧机械操纵卡滞-10X1传感器故障3.65×10-611X2离合器故障1.85×10-612X3升降舵轴承磨损变形1.87×10-513X4升降舵轴承间隙过大1.66×10-514X5左侧助力器卡滞1.00×10-515X6右侧助力器卡滞1.00×10-516X7左侧摇臂卡滞9.09×10-617X8左侧拉杆卡滞7.43×10-618X9方向盘卡滞1.05×10-520X10右侧摇臂卡滞9.09×10-621X11右侧拉杆卡滞7.43×10-6

(2) 可靠性模型及分析结果

将可靠性模型的输出量假定为顶事件T发生的概率，而11个基本事件发生的概率看做模型的输入量，且用Xi(i=1,2,…,11)来表示。11个输入变量均服从对数正态分布，其均值在表3最后一列给出，并假定所有输入变量的误差因子均为2。顶事件发生的概率估计为2.463×10-10，失效概率全局灵敏度指标确定的输入量的重要性排序为：η2η1η3η4η8η11η9η6η5η10η7。

概率安全评估的临界重要度和可靠性分析的全局灵敏度指标的对照如表4所示。

表4 算例2临界重要度和全局灵敏度指标的对照表

概率安全评估和可靠性分析所得的失效概率值基本一致；而基本事件的重要性排序并不一致，但重要的基本事件都是{X1,X2,X3,X4}，且基本事件{X5,…,X11}的重要性影响相差不大。

算例3 某型飞机的起落架系统主要由前、主起落架组成。前起落架固定在前机身，向机头方向收起到前起落架舱内，舱口有两块护板盖住。两个主起落架分别连接在左、右机翼主梁和前梁之间的支座上，向机身方向收到机翼的主起落架舱内，舱口有三块护板盖住。前、主起落架在正常情况下由液压系统来收放，当液压系统发生故障时，可采用应急系统放下前、主起落架。前、主起落架收上时，由上位锁锁住，放下时由收放作动筒的钢珠锁及液压油锁锁住。由于主起落架系统较为复杂，此处只针对“主起落架未到放下位置”这一故障进行分析。“主起落架未到放下位置”指的是主起落架放不下来，或者主起落架放下后锁不住。所建立的故障树如图4所示，各事件的名称及基本事件的发生概率如表5所示[9]。

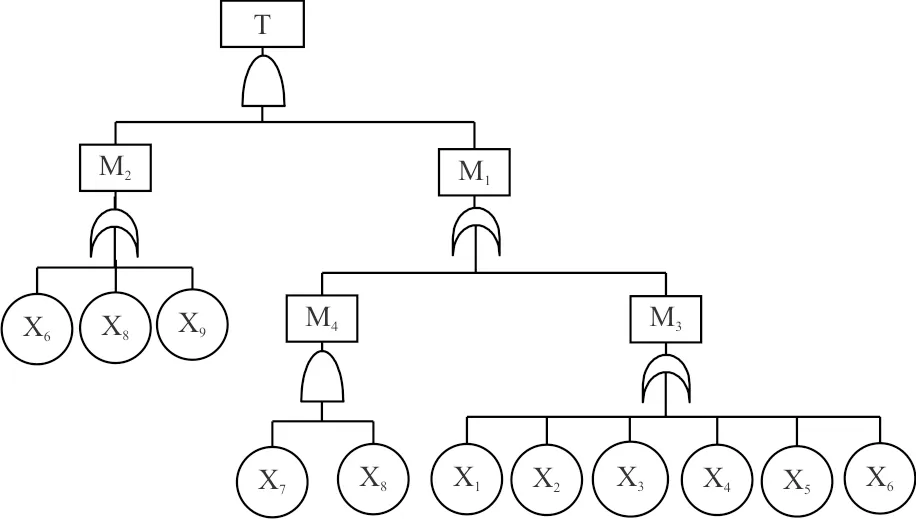
图4 主起落架未到放下位置的故障树

序号事件事件名称基本事件发生的概率1T主起落架未到放下位置-2M1正常情况下未到放下位置-3M2应急情况下未到放下位置-4M3主起落架放不下-5M4主起落架放下后锁不住-6X1液压电磁阀失效2.50×10-57X2开锁作动筒失效1.25×10-58X3护板锁打不开1.00×10-139X4护板作动筒失效7.15×10-510X5上位锁机构卡住2.00×10-1311X6主起落架收放作动筒失效1.25×10-512X7液压油锁失效2.00×10-813X8主起落架收放作动筒滚珠锁失效1.50×10-514X9应急放下时上位锁及护板锁打不开3.57×10-5

(1) 概率安全评估的分析结果

顶事件发生概率：g(q)≈1.250×10-5

临界重要度排序：Ic(6)>Ic(9)>Ic(4)>Ic(8)>Ic(1)>Ic(2)>Ic(7)>Ic(5)>Ic(3)

该故障树的最小割集较多，即造成顶事件发生的途径较多，因此顶事件发生的危险性高。降低基本事件X6、X8、X9的发生概率，可以大幅降低顶事件发生概率。

(2) 可靠性模型及分析结果

将可靠性模型的输出量假定为顶事件T发生的概率，而9个基本事件发生的概率看作模型的输入量，且同理用Xi(i=1,2,…,9)来表示。计算所得顶事件发生的概率为：1.252×10-5。考虑输入量不同的分布类型和分布参数，概率安全评估的临界重要度和四种情况下可靠性分析的全局灵敏度指标的结果如表6所示。

表6 算例3临界重要度和全局灵敏度指标的对照表

概率安全评估和可靠性分析所得的失效概率值基本一致；而从表6可以看出：四种情况下(Case1 输入量均为对数正态分布，误差因子为2；Case2输入量均为对数正态分布，误差因子为1.2；Case3输入量均为指数分布；Case4输入量均为均匀分布)可靠性分析的失效概率全局灵敏度指标所确定的基本事件的重要性排序与概率安全评估中的临界重要度的排序顺序完全不同，概率安全评估中的重要基本事件是{X6,X9,X8}，非重要基本事件是{X5,X3,X7}；而可靠性分析的重要基本事件均为{X3,X5}，四种情况下的基本变量的重要性排序顺序也基本一致。

从飞机结构的三个故障树的分析结果可以看出，概率安全评估和可靠性分析的失效概率值是基本一致的。而可靠性分析的失效概率全局灵敏度指标所确定的基本事件的重要性排序与概率安全评估中的临界重要度的排序顺序不一致，甚至会有颠覆性的排序结果。究其原因是基本事件发生概率的随机不确定性的引入，且随机分布类型和分布参数不同，重要性指标数值也不同。若想获得准确的全局灵敏度指标以高效快速指导可靠性设计，需获取精准的随机变量分布类型和分布参数，则需借助于先进的机器学习算法及Bayes理论。

4 结 论

(1) 概率安全评估和可靠性分析所得的失效概率值基本一致；而由于引入基本事件发生概率的随机性，会使得基本事件的重要性排序发生变化。

(2) 概率安全评估是在基本事件发生概率取其名义值时得出的，其鲁棒性欠缺，即当基本事件发生的概率值有微小扰动时，概率安全评估必须要进行重新分析和计算。相对而言，考虑基本事件发生概率的不确定性得出的可靠性结果会更加可靠。

(3) 对于基本事件相关或最小割集相交或不确定信息不完善等情况下，概率安全评估与可靠性分析之间的差异有待进一步考虑，这将为飞行器结构安全工程理论体系的完善依据。