飞机油箱水锤效应影响因素及其影响程度研究
韩璐,韩庆,杨爽
(1.西北工业大学 航空学院,西安 710072)(2.北京飞机维修工程有限公司 公务机服务部,北京 100621)
0 引 言
燃油系统是飞机暴露面积最大的系统[1],油箱则是构成燃油系统最重要的部件,水锤效应作为飞机油箱主要的损伤模式之一,指的是:当高速破片穿透有油液填充的油箱时,破片受到燃油的阻力,将自身的动能通过燃油传递到油箱壁板,从而引起油箱结构灾难性的破坏[2-3]。
水锤效应是一个复杂的流固耦合问题,完全采用理论方法来描述其整个过程十分困难,目前主要的研究方法是在试验基础上,通过理论和仿真模型分析,以一定的标准作为参量来衡量水锤效应的严重程度。在试验研究方面,R.E.Ball[4-5]首先利用22 mm口径步枪对立方体充液箱体进行冲击,通过测量不同能量等级的破片穿透时的流体压力和入射板应变,指出破片的入射角度和质量是影响其能量损失的主要因素,形状和动量对冲击波的运动影响不大;Masahiro Nishida等[6]完成了铝合金薄壁充水方管的打击试验,研究了壁板裂纹的扩展方式,指出最主要的影响因素为壁板材料的最大强度和子弹的直径;P.J.Disimile等[7]进行了钨合金、钢和铝合金破片撞击油箱的试验,测得了多个位置的压力时程;D.Varas等[8-9]进行了充液率分别为75%、100%的铝管水锤效应试验和数值仿真,并对比了同一充液率下不同破片速度(600、900 m/s)时液体中特定单元压力和壁板位移,结果表明,破片高速冲击时将带来更大的液体压力和壁板变形,充液率对靠近撞击点的壁板变形影响较大。
随着计算机仿真技术的不断进步,有限元方法开始被广泛的应用到水锤效应的数值模拟领域。P.Santini等[10]使用AUTODYN-2D模拟了涡轮发动机失效产生的三种形状破片撞击油箱的过程,结果表明,破片能量越大,产生的压力冲击波和穿孔越大;陈刚[11]利用MSC.DYTRAN研究了同一种模型在两种破片速度、弹头形状、入射角度入射时油箱前壁和后壁的应力应变情况;李亚智等[12]同样利用MSC.DYTRAN软件模拟了空箱和有水油箱在高速破片穿透情况下的动态响应,考虑了材料在高应变率下的弹塑性动态行为和几何非线性变形,指出液体存在时的流固耦合作用增加了油箱结构破坏的可能性;D.Varas等[13]分别使用ALE和SPH方法模拟了不同速度破片入射不同充液率的铝合金和复合材料油箱,获得了液体压力和箱壁变形的情况,分析得出液体压力是破片速度和测量位置的函数,而进出口壁板的应变主要取决于箱内流体的体积分数;陈亮等[2,14]采用PAM-CRASH模拟了不同打击方向下金属和复合材料油箱的水锤效应,分析了其损伤和破坏特性,指出复合材料箱体相比于金属箱体更容易在多墙体上发生整体破坏。
目前,油箱的水锤效应试验手段和数值仿真模拟方法已经较为成熟,但对于水锤效应影响因素的研究却仍然处在探索阶段,缺乏全面的归类,同时对每种因素的影响程度也没有进行系统地分析研究。
本文以某型飞机左机翼主油箱为研究对象,将可能对水锤效应造成影响的因素划分为破片速度、破片质量(材料)、破片形状、破片入射角度、入射方向和油箱内充液率六种;通过非线性有限元分析软件ANSYS/LS-DYNA,建立一个经过实验验证的等效油箱仿真模型;以毁伤评估中较为关注的破片剩余速度、液体中冲击波超压和前后壁板变形程度作为对比参数,分析上述因素对仿真模型水锤效应的影响,同时采用最小二乘法做多因素指数函数拟合,建立此种模拟条件下油箱入/出射壁板的变形位移计算公式,为燃油箱易损性评估提供数据支持。
1 水锤效应影响因素分析及仿真模型建立
1.1 水锤效应影响因素
水锤效应过程中,破片首先撞击、穿透油箱壁板,将自身的动能传递给箱内液体,产生冲击波超压并形成膨胀的空穴,沿破片运动轨迹排出的燃油形成一个向外扩展成辐射状的压力。压力不断地传递、反射和叠加到箱壁上使其变形或造成其碎裂,从而引起油箱漏油或机翼结构破坏;穿出后的破片将以一定的剩余速度继续毁伤下一个部件。同时,同一个破片击中飞机翼面后也可能经历不同的穿透过程。假设一个充液率为75%的立方体油箱在三种方向打击下的情况(如图1所示):D1方向为破片水平击中机翼直接进入液面然后穿出,穿透路径为壁板-箱内液态空间-壁板;D2方向为破片击中机翼上翼面后从下翼面穿出,穿透路径为壁板-箱内气相空间-箱内液态空间-壁板;D3方向为破片击中机翼下翼面后从上翼面穿出,穿透路径为壁板-箱内液态空间-箱内气相空间-壁板。

图1 破片打击方向示意图
因此,本文将影响水锤效应的因素划分为6种,即:破片速度、破片质量(材料),破片形状、入射角度、入射方向和油箱的充液率。利用LS-DYNA有限元软件对水锤效应影响因素及其影响程度进行研究。
6种不同因素不同入射条件下的研究方案如表1所示。
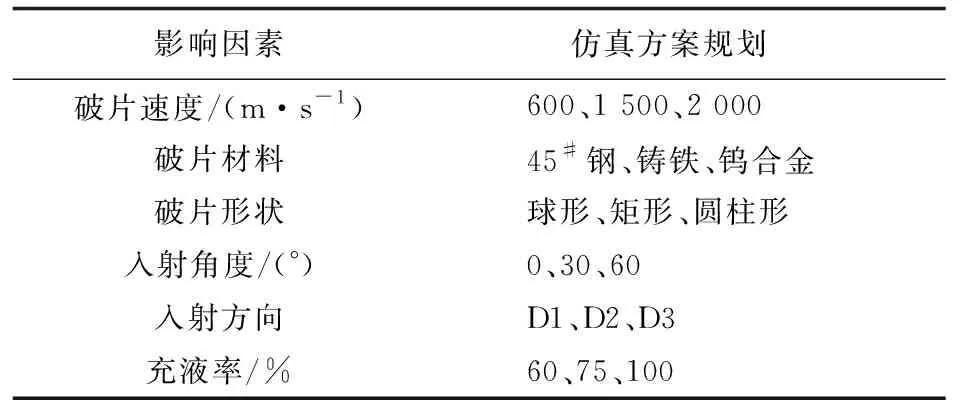
表1 水锤效应影响因素研究方案
1.2 有限元计算模型
为了验证模型的准确性,首先建立与文献[1]中所述试验相同尺寸和材料的100%充液箱体的有限元模型。模型包括箱体、破片、水和空气四部分(由于燃油的易燃易爆特性,直接进行高速冲击试验时不易控制且容易发生危险,在水锤效应试验中多采用与油液具有相似密度的水来替代航空煤油)。其中箱体由四块尺寸为750 mm×150 mm×2.5 mm的6063-T5铝合金方板以及两块厚度为30 mm的PMMA有机玻璃(试验中为了便于高速摄影记录水锤效应所形成的空穴)组成。模拟破片打击试验所使用的钢球质量8 g,直径12.5 mm,冲击速度为600和900 m/s。1/4模型共包含84 506个单元,网格类型全部采用六面体SOLID164,计算时长为8 ms,使用core i7-32GB计算机,计算耗时约为23 h,如图2所示。
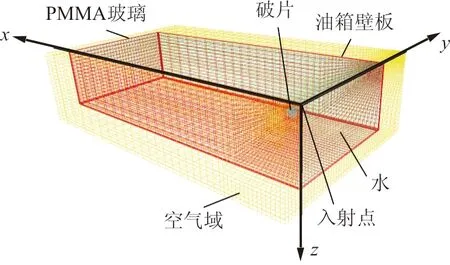
图2 有限元计算模型
1.3 箱体和破片有限元模型
为了在准确模拟的基础上减少计算成本,对弹着点周围的箱体网格进行加密,其余部分划分为随距离增加而稀疏的散射性网格。铝合金箱壁沿厚度方向划分为5个单元,沿长度和宽度方向划分为60和40个单元,最终箱体被划分为22 250个单元,选择Johnson-cook本构模型模拟。破片作为一个单独的part,网格尺寸比弹着点附近的箱体单元尺寸稍大,以便更好地模拟其与油箱壁板的接触。由于试验观察钢破片未产生塑性变形[1],采用弹性材料模型*MAT-ELASTIC对其进行模拟。
Johnson-cook本构模型适用于材料的高应变率塑性大变形,其失效准则的相关参数经过了大量的试验验证,能够较好地模拟破片的侵彻和冲击问题[15-16]。其屈服应力的表达式为
(1)
式中:A为准静态屈服应力;B、n为应变强化系数;C为应变率敏感系数;m为温度软化效应系数(式(1)中的A、B、n、c和m均可由试验确定);εe,p为等效塑性应变;T*m为实验温度。
(2)
T*m=(T-Tr)(Tm-Tr)-1
(3)
式中:Tr为室温;Tm为材料的融化温度。
箱体和破片的材料参数如表2所示[13]。
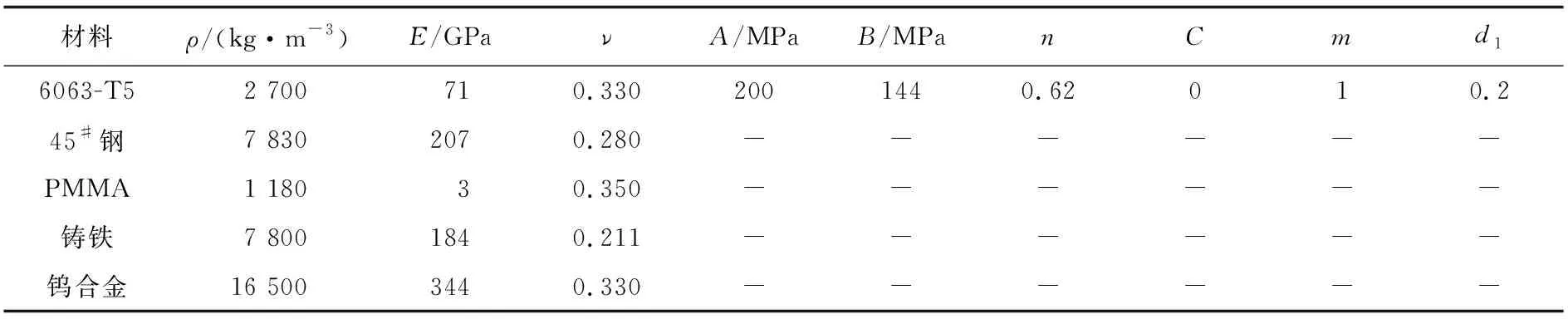
表2 箱体、破片材料模型参数
1.4 流体材料(空气和水)有限元模型
高速破片穿透入射壁板后,箱内液体在水锤效应的作用下将发生流动,网格会出现大变形,LS-DYNA内置的有限元单元算法中,Lagrange方法由于在计算过程中保持网格变形与材料的同步变形,在大变形问题中无法解决网格畸变,不适用于流体材料的描述。Euler方法虽然可以实现材料在空间网格中的流动,但是由于其不能明确地表述接触面和材料的边界,不适用于表述复杂的本构关系。Arbitrary Lagrange-Euler(ALE)方法综合了上述两种方法,能够动态地处理网格:先执行一个或几个Lagrange时间步的计算,此时单元网格将随着材料的流动而产生变形,然后进行Euler时间步计算,对内部单元重新划分网格,以应对计算过程中可能出现的大变形。
本文流体材料(空气和水)定义为单点多物质ALE(*SECTION_SOLID,ELFORM=11)单元,通过*ALE_MULTI-MATERIAL_GROUP关键字把空气和水绑定在一个单元算法里,在建模时将水域和空气域共节点。选用9号材料模型*MAT_NULL和*EOS_GRUNEISEN状态方程对流体材料进行模拟,利用*CONSTRAINED_LAGRANGE_IN_SOLID和*CONTROL_ALE关键字实现流固耦合定义和ALE方法的选项控制。最终,流体材料一共被划分成了62 040个单元,其材料参数如表3所示[13]。

表3 水、空气材料模型参数
1.5 模型验证
参考D.Varas等[1]的试验结果,通过对液体中特定位置的压力-时间历程和水锤效应过程中形成空穴过程的对比,来验证模型的正确性。文献[1]中试验测试模型简图如图3所示,PTn和PTf为两个试验压力探测点,采用传感器进行测量。试验所得两个探测点的压力-时间历程数据如图4(a)所示;选择有限元模型中相同的压力探测位置PTn和PTf的两个网格单元,仿真所得压力-时间历程对比如图4(b)所示。
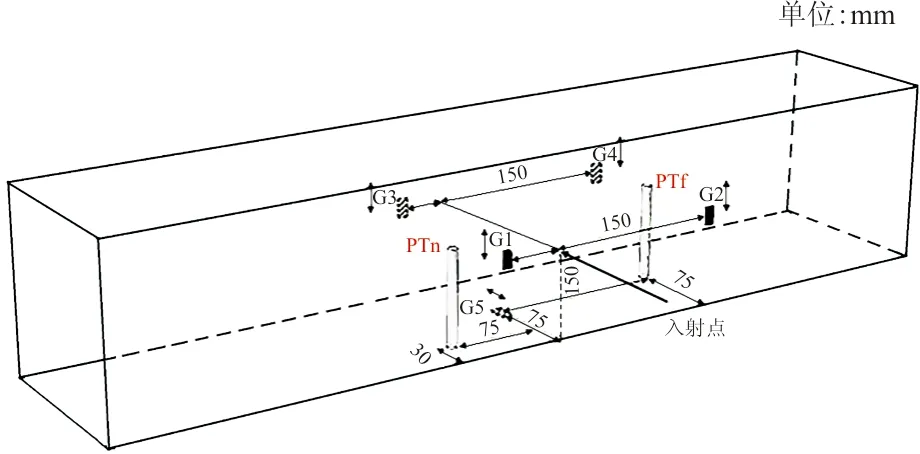
图3 试验模型简图
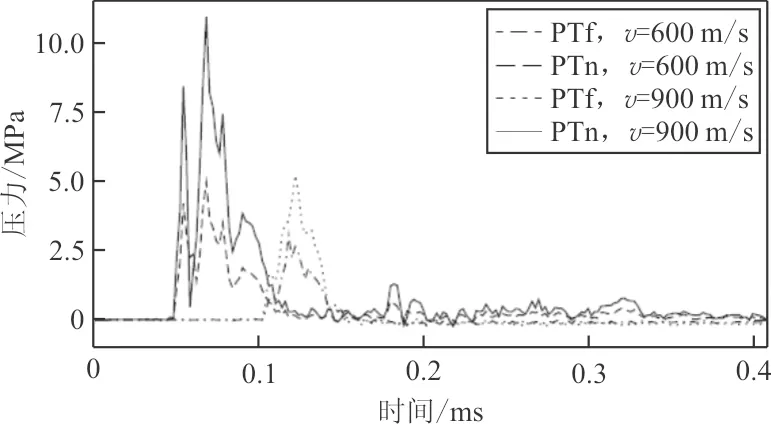
(a) 实验测得PTn和PTf处液体压力-时间历程

(b) 仿真测试PTn和PTf处液体压力-时间历程
从图4可以看出:图4(a)中液体压力由传感器捕获,因此出现了多个峰值,图4(b)中数值模拟结果则呈现单个峰值;当破片速度分别为600和900 m/s时,仿真与试验所得液体压力峰值误差在PTn位置分别为2.23%和3.84%,在PTf位置分别为4.0%和5.3%。
仿真计算得到的液体空穴效应与试验对比如图5所示,可以看出:在相同采样时刻,通过有限元计算得到的空穴形状与文献[1]中所得高速摄影结果趋势一致,表明本文有限元模型能够在误差允许范围内模拟油箱的水锤效应,可用于油箱水锤效应的规律性研究。

图5 空穴形成过程对比
2 水锤效应影响程度研究
以某型飞机1号左机翼主油箱为研究对象来研究水锤效应的影响因素及其影响程度。将油箱等效为一个尺寸为1 000 mm×200 mm×300 mm的铝合金长方形箱体,壁板厚度为2.5 mm。选择破片速度随时间的衰减历程、PTm(150 mm,100 mm,0 mm)处冲击波超压和油箱壁板变形作为对比参量。其中入射和出射壁板位移测量单元均位于油箱中心高度,沿x轴方向分布。1/4模型总单元数为157 535,网格全部采用六面体SOLID164类型。
2.1 破片速度对水锤效应的影响
选用φ20 mm的45#钢材料球形破片,垂直入射冲击100%充液的油箱,冲击速度分别为900、1 500和2 000 m/s,仿真所得破片速度衰减、PTm处液体压力-时间历程和前后壁板位移如图6所示。
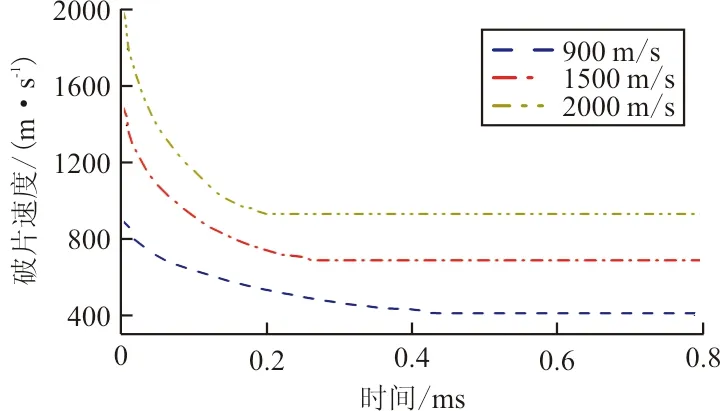
(a) 破片速度-时间历程

(b) PTm处压力-时间历程

(c) 入射壁板变形
从图6(a)可以看出:破片速度在穿透入射壁板时急剧下降,而后在液体中平缓衰减,穿出时由于破片前方液体提前对出射壁板的破坏作用,破片速度仅发生了小幅度的衰减;随着破片速度的增加,其在水中运动的时间历程明显缩短,剩余速度显著增加,但速度的衰减程度并无很大差异,例如破片以1 500和2 000 m/s的速度入射时,其穿出时间相较900 m/s入射时分别提前了0.15和0.24 ms,剩余速度分别提高了64.3%和126.5%;但三种速度下破片的速度衰减程度分别为52.5%、53.3%和54.4%,最大差异仅为3.62%。
从图6(b)可以看出:破片入水后形成的冲击波在水中以一定的速度迅速扩张,所经之处带来较高的压力,探测点PTm的压力在冲击波到达时突然增加,而后逐渐衰减为0;破片速度的增加增大了冲击波的波速,使其更早地到达PTm位置;同时,破片速度的增加显著增大了冲击波超压的峰值,例如,破片速度为1 500和2 000 m/s时的压力峰值较900 m/s时分别增加了137.04%和304.51%,而到达时间分别提前了0.010和0.015 ms。
对比图6(c)和图6(d)可以看出:出射壁板的变形明显大于入射壁板,以1 500 m/s速度入射为例,入射壁板的变形从距离入射点左右280 mm的范围内开始,最大变形约为36 mm;而出射壁板在距离入射点左右350 mm的位置开始,其最大值为50 mm。因此在水锤效应中应当更关注前者的变形情况,在油箱设计中也应针对常见的交会姿态,对出射壁板加以防护或在设计时保留更大的变形余度。随着破片入射速度的增加,前后壁板的变形范围和变形程度都有明显增加,以变形程度为例,1 500和2 000 m/s速度入射时,前后壁板的最大变形分别较900 m/s入射时增加了9、20和7、25 mm。
破片入射速度的增加显著地提高了其穿出时的剩余速度,增加了水中冲击波波速和超压峰值,进而对壁板造成了更为严重的破坏,因此破片入射速度的增加将显著增强水锤效应的破坏作用。
2.2 破片质量(材料)对水锤效应的影响
相同形状尺寸、不同材料的破片具有不同的质量,因此将破片质量与破片材料对水锤效应的影响研究合并,以三个直径为φ20 mm的球形45#钢、铸铁、钨合金破片作为研究对象,均以900 m/s的速度垂直入射充液率为100%的油箱,破片的材料参数设置如表2所示。不同材料破片入射时仿真所得的破片速度衰减、PTm处压力-时间历程和入/出射壁板位移-时间历程如图7所示。
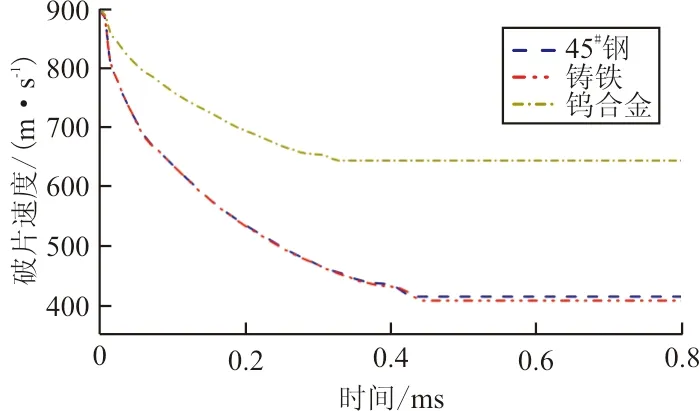
(a) 破片速度-时间历程

(b) PTm处压力-时间历程
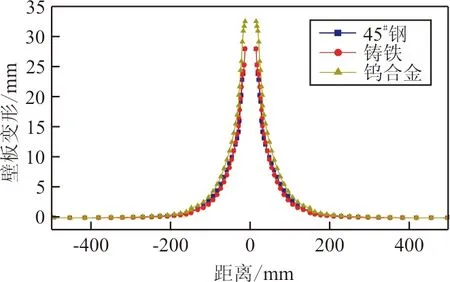
(c) 入射壁板变形
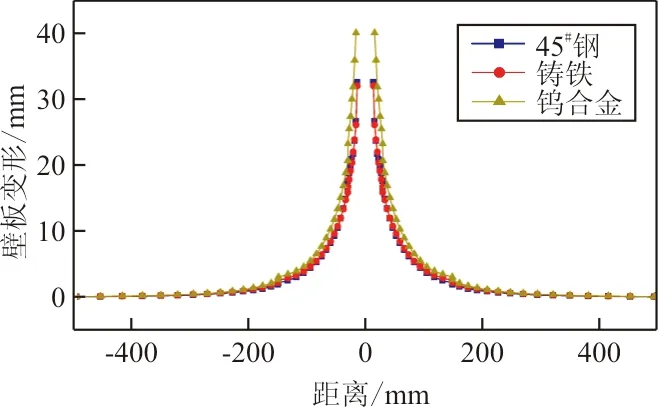
(d) 出射壁板变形
从图7可以看出:无论是液体压力、速度衰减和前后壁板的变形,45#钢和铸铁都获得了较为接近的结果,而钨合金破片则造成了更大的剩余速度、峰值压力和前后壁板变形。钨合金破片在穿透入射壁板时即获得了约为845 m/s的剩余速度,进而使PTm处的压力峰值较铸铁和45#钢增加了19.2%;相同体积和形状的钨合金破片入射时,前后壁板最大变形分别增加了21.8%和23.9%。
三种材料破片中,铸铁和45#钢相比,密度相似,弹性模量和泊松比等其余材料参数不同;钨合金与铸铁、45#钢相比,具有更大的材料密度,即具有更大的质量。结合图7所得结果,可知:相比于其他材料参数,破片的材料密度对水锤效应的影响更为显著;相同体积时,破片密度(质量)越大,水锤效应越严重。
2.3 破片形状对水锤效应的影响
为了研究破片形状对水锤效应的影响,选择具有相同体积和迎风面积的球形、长方形、圆柱形45#钢破片为研究对象,其中球形45#钢破片直径φ20 mm、矩形破片尺寸17.72 mm×17.72 mm×13.33 mm、圆柱形破片尺寸为φ20 mm×13.33 mm,均以900 m/s的速度垂直入射充液率为100%的油箱。仿真所得破片速度衰减、PTm处压力-时间历程和入/出射壁板位移-时间历程如图8所示。
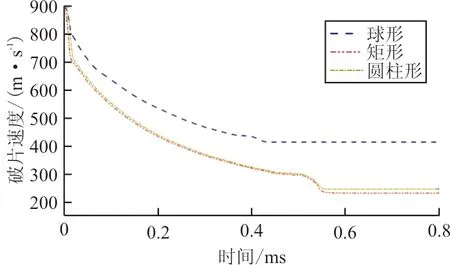
(a) 破片速度-时间历程
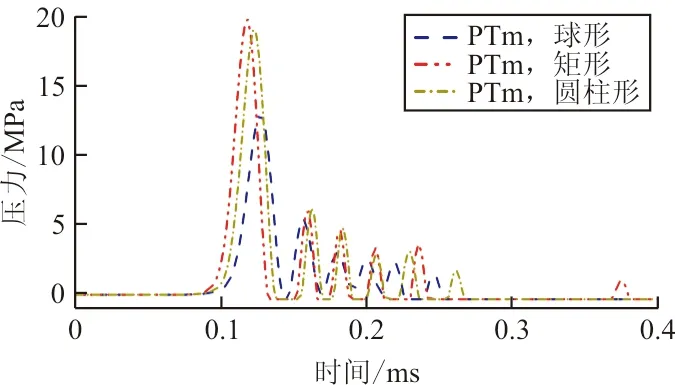
(b) PTm处压力-时间历程

(c) 入射壁板变形

(d) 出射壁板变形
从图8(a)可以看出:由于球形破片与入射壁板的平均接触面积小于矩形和圆柱形,其在入射阶段获得了更大的剩余速度,约为820 m/s;同时,虽然球形破片与矩形、圆柱形破片具有相同的迎风面积,其在水中的速度衰减程度与后二者并不相同,在图8(a)中,球形破片速度在水中衰减程度约为45.12%,而矩形和圆柱形破片为56.94%,二者差异达到了11.82%,表明破片的速度衰减不仅取决于迎风面积,也与弹头形状相关。
液体压力取决于破片入水后产生的冲击波波速,而冲击波波速则取决于破片入水时的剩余速度。从图8(a)和图8(b)可以看出:球形破片在穿透入射壁板后虽然具有最高的剩余速度,其在PTm处引起的液体压力却最小,表明破片的形状对其入水时产生的冲击波超压具有不可忽视的影响。
从图8(c)和图8(d)可以看出:球形破片引起的壁板变形范围和程度均最小,矩形和圆柱形破片入射时前后壁板的变形范围几乎相同,但在穿孔周围,矩形破片获得了更大的位移,以出射壁板为例,球形破片入射时壁板变形从距离箱壁边缘240 mm的位置开始,在穿孔周围约为32.5 mm;而矩形和圆柱形破片入射时,变形均从距离箱壁两端200 mm的范围开始,在穿孔周围的位移分别达到了42和39.4 mm,这是由于不同的穿孔形状使裂纹扩展方向发生变化,从而造成穿孔周围花瓣状损伤的屈曲程度的差异。
由此可见,破片形状对破片速度衰减、液体压力峰值及油箱壁板变形均具有一定的影响,在水锤效应影响因素研究中应当予以充分考虑。
2.4 破片入射角度对水锤效应的影响
实际作战中,破片通常不会垂直地射入油箱,而是以一定的角度入射。入射角度将会改变破片的运动路径,不仅会在穿透入/出射壁板时影响破片的剩余速度,改变其在弹道方向上的投影面积,同时也会改变其在液体中的运动时间。为了研究破片入射角度对水锤效应的影响,选用φ20 mm的球形45#钢破片,以900 m/s的速度,分别以与入射壁板法线夹角0°、30°和60°的入射方向,通过图2中的入射点从左侧在xy平面内打击100%充液油箱。建立如图2中关于xy平面对称的1/2仿真模型,所得破片速度衰减、PTm处压力-时间历程和入/出射壁板位移-时间历程如图9所示。
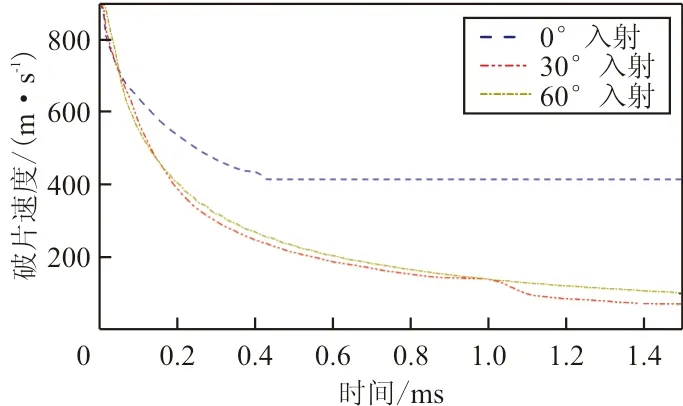
(a) 破片速度-时间历程
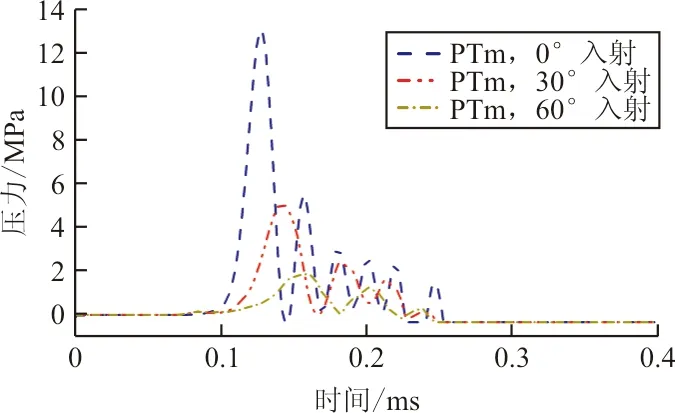
(b) PTm处压力-时间历程

(c) 入射壁板变形
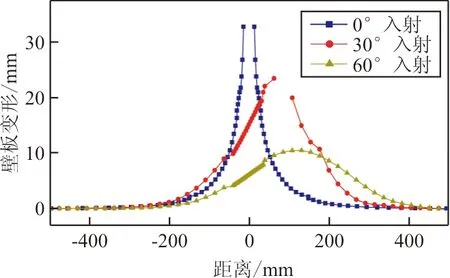
(d) 出射壁板变形
针对本文中研究的油箱模型,入射角度的增加将会增加破片在水中的运动路程,使其速度发生更大的衰减。从图9(a)可以看出:垂直入射时破片约在0.38 ms时穿出,剩余速度约为420 m/s;30°入射时,破片在1.4 ms时穿透出射壁板,剩余速度约为80 m/s;而60°入射时,破片在液体中速度衰减至0,将所有动能传递给了油箱内液体。
破片入射角度的增加造成了PTm与破片轨迹之间的距离的增加,因此随着入射角度的增加,PTm处的压力峰值不断减小,且到达压力峰值的时间不断增大。以破片30°入射时为例,PTm处出现压力峰值的时间较垂直入射时延迟了0.015 ms,压力峰值减小了约7.7 MPa。即入射角度对特定位置的液体压力具有不同的影响,在油箱水锤效应评估中应针对特殊的位置需求,考虑入射角度带来的影响。
破片的倾斜入射将使入水后形成的空穴不再对如图2所示的yz平面对称,从而使由于空穴挤压而引起的壁板变形亦不再对称。从图9(c)可以看出:入射壁板以穿孔为分界,出现了断层变形,以60°入射为例,穿孔右侧的最大位移约为33.2 mm,较左侧增加了164%。而在出射壁板上,随着入射角度的增加,壁板发生变形的范围不断右移,且最大值不断减小。从图9(d)可以看出:30°入射时,出射壁板的最大变形发生在距离右端420 mm处,约为22.5 mm;而60°入射时,最大变形发生在距离右端370 mm处,值约为11.3 mm。
由此可见,破片的斜入射将显著影响破片的剩余速度,同时造成入/出射壁板变形范围的改变。
2.5 油箱充液率对水锤效应的影响
实际飞行任务中,飞机油箱内的燃油并不是常处于满油量状态,为了研究充液率对水锤效应的影响,以60%、75%和100%充液三个状态,研究充液率对水锤效应的影响。选用φ20 mm的球形45#钢破片,垂直入射速度为900 m/s。仿真所得破片速度衰减、PTm处压力-时间历程和入/出射壁板位移-时间历程如图10所示。
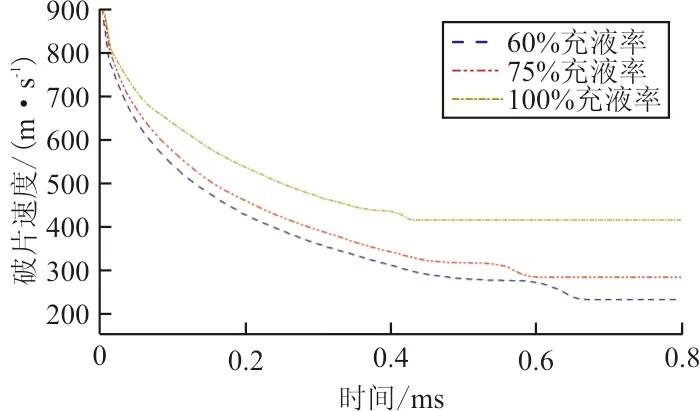
(a) 破片速度-时间历程
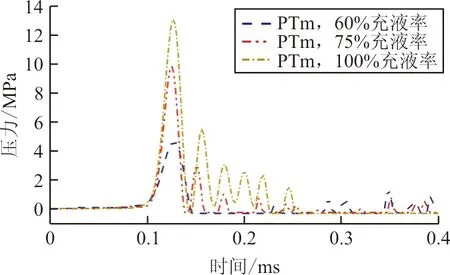
(b) PTm处压力-时间历程

(d) 出射壁板变形
从图10可以看出:无论是破片的速度衰减、液体中压力峰值还是前后壁板变形均与油箱内充液率呈现正相关。以破片速度衰减和出射壁板变形为例,100%充液时,破片穿透油箱后的剩余速度分别为75%和60%充液时的1.5倍和1.75倍,出射壁板的最大变形则分别为75%和60%充液时的113.33%和130.77%。这里假设一种极端情况:充液率为0%,即油箱空油,那么箱内液体压力可以看作为0,壁板位移也将只是由穿透作用而引起的变形。
由此可见,水锤效应主要是由于破片在液体中运动时发生的能量传递,随着充液率的增加,油箱水锤效应会不断增大。在油路设计时应当减小高危部位的油位,从而降低油箱易损性。
2.6 破片入射方向对水锤效应的影响
对于非满液油箱,同一个破片击中飞机翼面后可能经历不同的穿透过程。以1.1节中所述的D1、D2和D3三个方向为例,研究破片入射方向对水锤效应的影响。为了使破片具有相同的路程,修改模型中长度方向和高度方向的尺寸,建立一个边长为200 mm的75%充液立方体油箱,选用φ20 mm的球形45#钢破片,从入射壁板的中心以900 m/s的速度垂直入射,PTm位置选择在立方体的几何中心。仿真所得破片速度衰减、PTm处压力-时间历程和入/出射壁板位移-时间历程如图11所示。
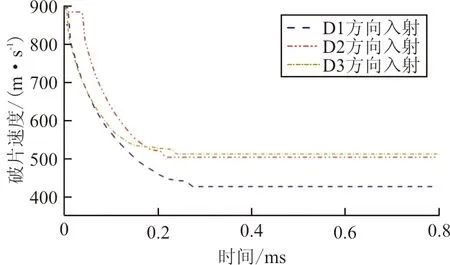
(a) 破片速度-时间历程

(b) PTm处压力-时间历程

(c) 入射壁板变形

(d) 出射壁板变形
从图11(a)可以看出:D1方向入射时,破片经历了穿透入射壁板速度衰减、全程燃油阻滞速度衰减、穿透出射壁板速度衰减和穿出后的匀速运动;D2方向入射时,破片经历了穿透入射壁板速度衰减、箱内气相空间空气阻力导致的速度微小下降、液相空间燃油阻滞速度衰减、穿透出射壁板速度衰减和穿出后的匀速运动;D3方向入射时,破片经历了穿透入射壁板速度衰减、液相空间燃油阻滞速度衰减、箱内气相空间中燃油飞溅导致的缓慢减速、穿透出射壁板速度衰减和穿出后的匀速运动。D3方向入射时破片的速度损失最少,剩余速度为511.2 m/s,D1方向入射时破片速度衰减最大,剩余速度约为425.4%,这是由于D1方向入射时,破片在液体中穿行的距离最长,受到了较大的阻滞作用。
从图11(b)可以看出:虽然PTm与破片的0时刻位置距离相同,但是D2方向入射时PTm出现压力激增的时刻较D1和D3方向入射时延迟了约0.013 ms,但获得了更大的峰值,约为42 MPa。这一结果进一步证明了PTm处测得的液体压力来自于破片入水后产生的冲进波;另外,由于箱体为75%充液,破片从D3方向入水时,冲击波到达PTm的衰减路径仅为D1和D2方向入射时的一半,因此其获得了更大的超压,表明冲击波在水中是不断衰减的。
对比图11(c)和图11(d)可以看出:D2方向入射时,由于入射壁板未与液体直接接触,变形只集中在其穿孔附近约为3 mm,而出射壁板受到液体的挤压,获得了约为26 mm的最大变形;相反,D3方向入射时,入射壁板由于液体的作用获得了更大的变形,约为18.6 mm,而出射壁板只是单纯受到弹丸的冲击变形,约为4 mm;而D1方向入射时,由于破片受到燃油更持久的阻滞作用,加剧了流固耦合作用对油箱壁板的冲击,使入/出射壁板均获得了最大的变形程度和变形范围,以出射壁板为例,变形范围覆盖了全壁板,最大值则达到了43 mm。
因此,破片从不同方向入射将会引发不同的穿透路径,对水锤效应有一定的影响。破片在燃油中穿行的距离越远,传递给燃油的能量则越多,由流固耦合引发的箱壁变形毁伤也越剧烈。
2.7 各因素影响程度分析
经过对上述各因素的模拟及分析,可以看出:破片速度、材料(质量)、形状以及油箱充液率是直接影响油箱水锤效应的;破片入射角度、入射方向直接影响破片在油液中的运动路径,从而间接影响水锤效应。因此,以无量纲化的速度、密度、迎风面积、相对运动路程及充液率作为自变量,以油箱的前后壁板的最大变形比Den/Lw和Dex/Lw为因变量,做多因素指数函数拟合分析,可得:
(4)
(5)
式中:Vf为破片速度;Ct为油箱壁板材料的声速;ρf为破片的密度;ρt为油箱壁板材料的密度;Af为破片的迎风面积;As为等效球形破片截面积;Fr为充液率;Lf为破片在液体中的路程;Lw为油箱宽度。
公式(4)和公式(5)是针对于本文算例中尺寸油箱获得的半经验式,适用打击速度范围为900~2 000 m/s。同时,公式对函数形式的选择以及初值的选定有较强的依赖性。对不同尺寸、材料或其他结构形式的油箱,仍需经过大量的试验或者数值模拟,重新选择更合适的方程对其进行拟合。
3 结 论
(1) 对于相同尺寸、充液率的油箱,水锤效应的破坏程度随破片入射速度的增加而显著增强,这是由于具有较高速度的破片能够将更大的能量传递给燃油,进一步导致壁板遭受更大的液压冲击。
(2) 对于相同尺寸、充液率的油箱,在相同形状和体积、不同材料破片入射时,水锤效应的破坏能力随破片质量的增大而加剧,其中起主要影响作用的是材料密度。
(3) 破片形状不仅影响其对油箱壁板的穿透、影响其在油液中的衰减,同时也间接影响壁板变形:球形破片获得了更大的剩余速度,而矩形破片造成了更严重的液体压力和壁板位移。
(4) 水锤效应的产生主要是由于破片在液体中运动时发生的能量传递,与空油箱相比,充液油箱在破片高速冲击下的毁伤情况更为严重;液体压力和壁板位移均随着充液率的增加而显著增加,箱体的变形主要集中在与液体直接接触的区域。
(5) 破片在油液中的运动路径将影响其剩余速度,增大箱内油液所吸收的能量,因此破片入射角度、入射方向也是水锤效应不可忽略的影响因素。

