辊位参数对大径厚比电阻焊管成形的影响

胡盛德 余 昊 陈 俊 李立新 潘成刚

(武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，湖北 武汉 430081)

随着钢结构行业的快速发展，一些大口径薄壁焊管因单位质量轻，截面特性优而逐渐受到钢结构设计者的青睐，如光伏电站太阳能支撑管、核主泵屏蔽套坯管等。对高频直缝焊管，可稳定生产的径厚比一般为15～90，但当圆管径厚比为90时，属于大径厚比的特殊圆管，这类管在使用连续辊弯排辊成形生产时边缘位移量大，极易出现边浪、焊接不稳定等问题，难以保证焊管的综合质量[1- 4]。另外，不合理的变形量分配还会加速对轧辊的磨损、加剧“反弯”现象而增加不必要的能耗[5]。因此，为了确定合理的成形工艺，本文通过有限元仿真分析研究了辊位参数对大口径薄壁管成形的影响。研究参考了某种规格产品原始下山量及辊位参数，以成形过程中板带横截面纵向应变的方差最小、等效塑性应变均匀、待焊边部形态好和产品无边浪为目标，对下山量和底辊辊位参数进行优化，并在此基础上，以待焊边部形态好、反弯最小为目标对轧辊开口度进行优化。

1 动力学基本理论知识

求解域动力显式方程可表示成：

(1)

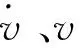
运用中心差分法求解式(1)。时刻的离散速度、加速度中心差分公式分别为：

(2)

(3)

将式(2)、式(3)代入式(1)，可得求解各个离散时间点位移值的递推公式：

(4)

为了使该算法趋于稳定值[6- 7]，运用显示算法直接求解，在条件稳定的要求下，需要较小的时间步，且保持状态足够稳定，即时间步长必须小于该问题求解方程性质根据 Courant- Fried Richs- Levy稳定性准则所决定的临界值。在非线性和非线性接触存在内力矢量中包含的内力可以不用在检查中收敛。

2 排辊成形有限元模型

在建立弹塑性有限元模型的过程中，准备φ508 mm的产品，以HFW660直缝焊管排辊成形为例。参考生产实际，成形带钢尺寸选为24 000 mm×1 580 mm×5.6 mm，材料为X60管线钢，其弹性模量E=210 GPa，泊松比μ=0.3，密度ρ=7 800 kg/m3；网格采用三维4节点有限薄膜应变壳单元(S4R)划分；实际生产速度为0.2 m/s。为了减少计算时间同时保证较高的计算精度，研究中尝试了不同的板带速度，发现速度设为2 m/s较为合适，此时满足系统动能小于内能5%的要求[6- 7]；选择通用接触，轧辊设为主控面；采用库伦摩擦，摩擦因数设为0.1；排辊成形过程中，板带中心只能沿成形方向前进，横向不能有位移，因此设置板带中心线上节点的横向位移为0。考虑到生产过程中轧辊的变形极小，设置轧辊为刚体[5]，其网格划分采用3节点三维三角形刚体单元(R3D3)。由于对称性，只需建立1/2模型[8]，如图1所示。

图1 HFW焊管排辊成形过程有限元模型Fig.1 FEM model of cage- roll forming for HFW pipes

3 仿真结果及变形规律讨论

3.1 试验验证

为了验证有限元模型的正确性，对比板带关键位置的开口度和板带边缘深度的模拟值和计算值，如表1所示。其中开口度是指板带两边缘之间的水平距离，位于变形板带的横截平面中，而板带边缘距中心处的竖直距离则是指边缘深度。选取对比点为：预成形段P1、P2处、线成形段L1、L3处，其到夹送辊纵向距离分别为ZP1=4 560 mm、ZP2=7 100 mm、ZL1=10 400 mm、ZL3=16 600 mm，如图2所示。

由表1可见，边缘深度的误差值在1.2%～2.6%之间，开口度的误差为1.2%～3.5%之间。与实际生产的吻合度较高，说明了有限元模型的可靠性。

表1 关键位置边缘深度和开口度的模拟值与实测值的对比Table 1 Comparison of simulated and measured values of height of cross- section and opening value at different positions

图2 成形方向测量位置示意图Fig.2 Schematic diagram of measurement positions along forming direction

3.2 辊位参数对大径厚比高频焊管成形的影响

为了保证钢板边部纵向应变尽量小和缩短成形机组长度，HFW660直缝焊管排辊成形通常采用下山法成形，所谓下山法就是在成形过程中板带底部呈逐渐下降趋势[1]。本文将HFW660直缝焊管排辊成形机组的轧辊分为两部分：轧辊的约束开口度和下山量，及其约束成形底线。夹送辊、预成形內辊、大压下辊往往存在于约束成形底线及下山量的轧辊中，并且线成形段支承辊及內辊、精成形段轧辊在其中也有不少涉及。约束成形底线的轧辊辊位参数变化的表现形式很多，本文采用下山量H及下山曲线的变化来表示。在试验中发现，在采用下山法成形直缝焊管情况下，成形底线体现在预成形段和线成形段有一定幅度的减少，因此，本文以精成形入口处带钢中心线与夹送辊带钢中心线间的竖直距离来表示下山量H，如图3所示。同时，以开口度W的增减来约束开口度轧辊的辊位参数值，且约束开口度的轧辊主要有弯边辊、预成形和线成形段的排辊。

3.2.1 下山量及下山曲线的影响

采用下山法成形时，为了达到最佳成形效果，约束成形底线及下山量的轧辊底部的连线呈圆滑过渡的曲线，从而使下山成形阻力降到最低，因此最优的下山曲线理论上符合二次函数形式，可以用二次曲线来拟合[1]。坐标原点O设在板带中心的夹送棍处，x轴正向设为板带轧制成形方向，竖直向上为y轴正向建立坐标系(见图3)，设成形底线的曲线函数为：

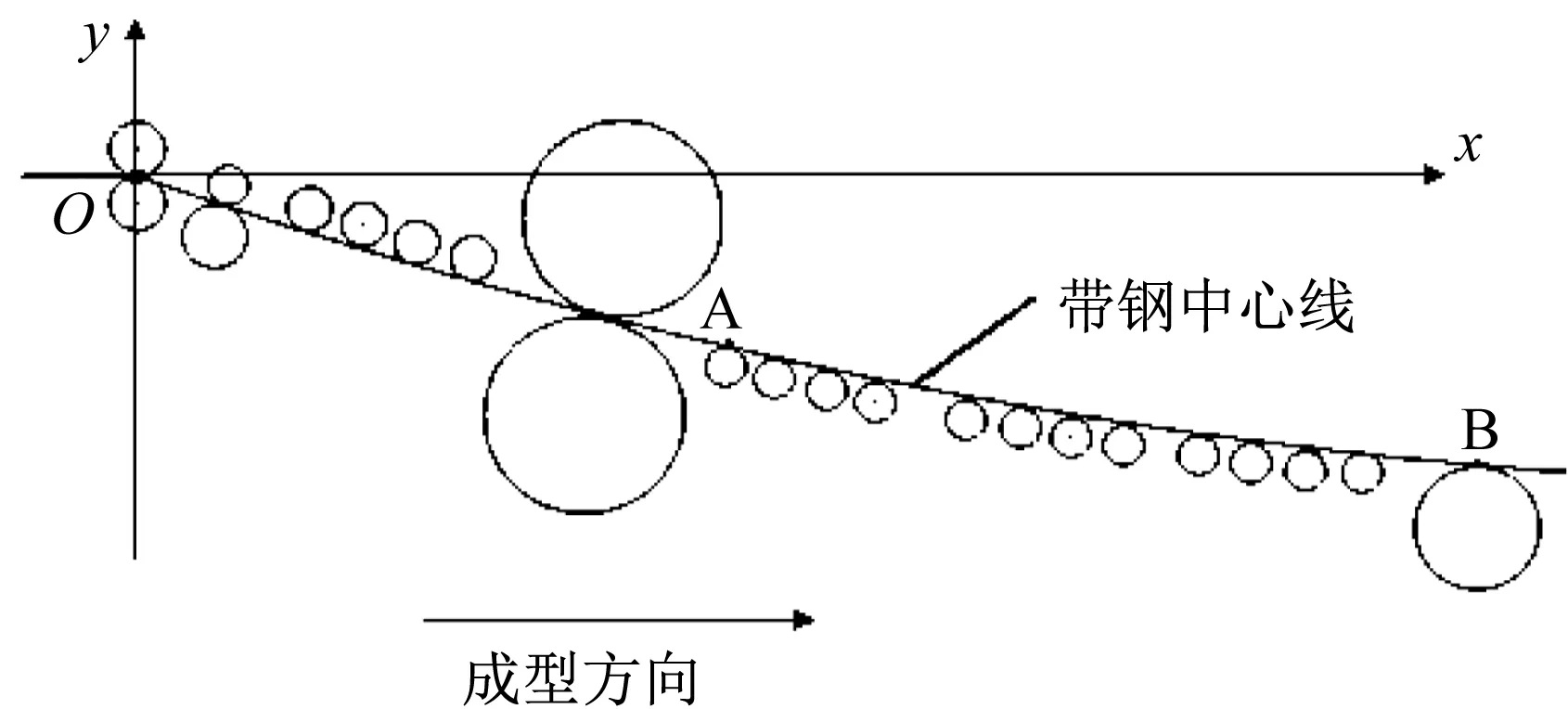
图3 下山法成形底线示意图Fig.3 Schematic diagram of downhill method in roll formation

y=ax2+bx+c

(5)

参考原始辊位参数，固定夹送辊、保持预成形段和线成形段下山量的比例不变，对下山量为H=0.8D(D为圆管直径)的φ508 mm直缝焊管的原始辊位成形底线，利用Origin软件进行二次曲线拟合，得到：

y=6.299 87×10-7x2-0.034 43x

(6)

不同焊管生产单位根据成品尺寸选择的下山量不同，但一般在H=(0.4～1.2)D范围内。为了进一步比较不同下山量及下山曲线对直缝焊管成形的影响，除原始辊位下山量外，本文还选择H=0.4D、0.6D、1.0D、1.2D等下山量，采用同样的方法拟合下山曲线，所有下山曲线的函数系数见表2，其所对应的函数图像(成形底线)如图4所示。

表2 下山曲线函数系数Table 2 Functional coefficients of downhill curves

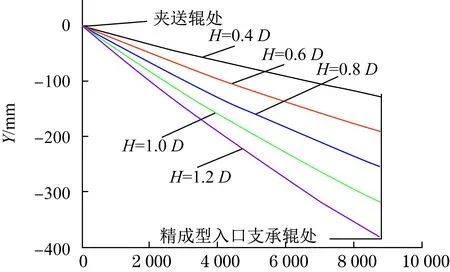
图4 下山曲线函数图像Fig.4 Function curves of downhill formation

将约束成形底线及下山量的轧辊如弯边辊、预成型上辊、大压下辊等的辊位横坐标x值代入上述下山曲线函数，得到辊位新的纵坐标y值，以此来指导轧辊的上下调整，保持其他成形参数不变，进行有限元模拟计算，得到下山效果、等效塑性应变及待焊边部形态，如图5～图9所示。

由图5可见，H=0.4D下山量时，管坯最大等效塑性应变值为0.407 7；出精成形后的待焊管坯边部鼓包边浪比较明显。

由图6可以看出，H=0.6D下山量下，管坯最大等效塑性应变值为0.382 3；出精成形后的待焊管坯边部有鼓包出现。

图5 H=0.4D时的(a)下山效果、等效塑性应变及(b)待焊边部形态Fig.5 (a)Downhill effect, equivalent plastic strain and (b) shape of the pending edge when H is equal to 0.4D

图6 H=0.6D时的(a)下山效果、等效塑性应变及(b)待焊边部形态Fig.6 (a)Downhill effect, equivalent plastic strain and (b) shape of the pending edge when H is equal to 0.6D

由图7可见，原始下山量下管坯最大等效塑性应变值为0.371 2；出精成形后的待焊管坯边部亦有轻微鼓包产生。

由图8看出，H=1.0D下山量下，管坯最大等效塑性应变值为0.350 5；出精成形后的待焊管坯边部较平直，成形状态良好。

由图9可见，H=1.2D下山量下，管坯最大等效塑性应变值为0.394 1；待焊管坯边部有较轻微边浪出现。

纵向应变不均匀是引起带钢边浪等缺陷的主要原因，除等效应变和待焊边部形态外，模拟还给出了因压下量大而导致应变不均匀位置的板带横截面纵向应变的方差结果，图10所示为不同下山量下，弯边辊处(BD)及Fp1、Fp2、Fp3精成形3个道次处带钢横截面上各点纵向应变的方差变化。可见，下山量的变化对应变方差有一定影响，其中精成形的首个道次处变化最大。从整个模拟过程看，下山量过大或者过小，均会导致4个位置带钢横截面上纵向应变方差变大，在H=1.0D时，方差最小，板带变形最均匀。

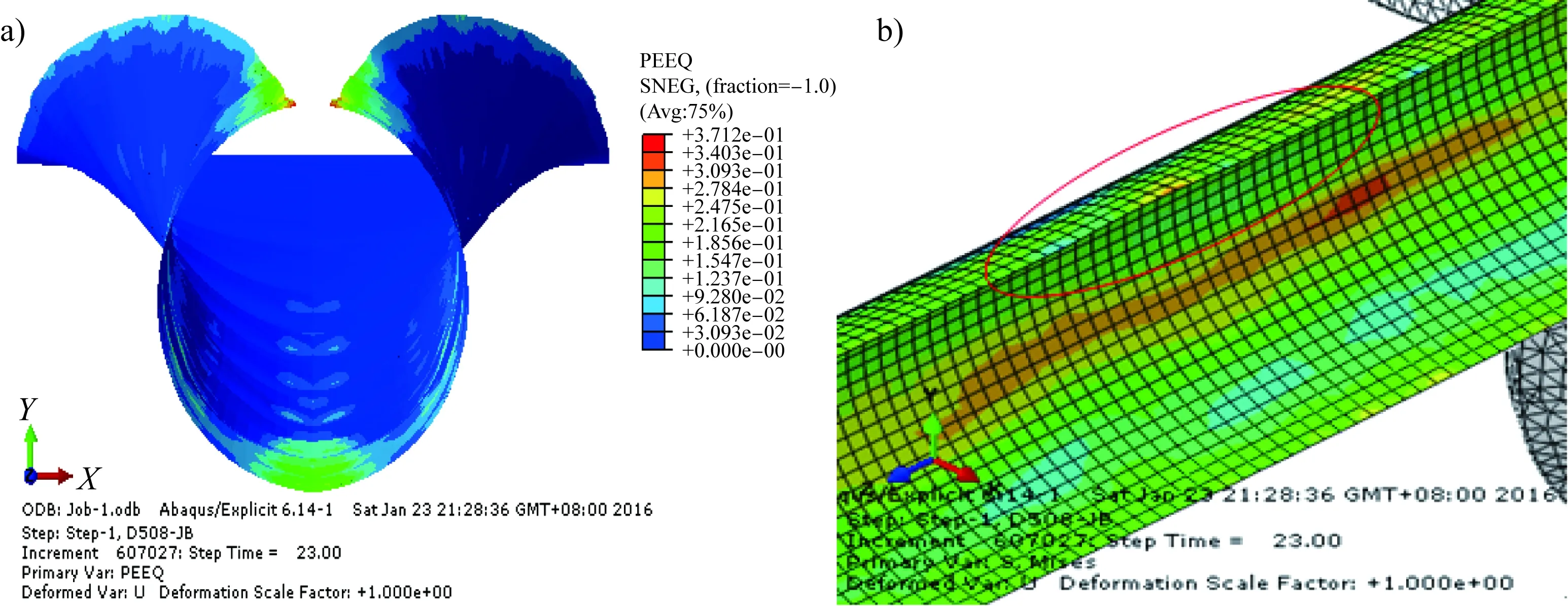
图7 H=0.8D时的(a)下山效果、等效塑性应变及(b)待焊边部形态Fig.7 (a) Downhill effect, equivalent plastic strain and (b) shape of the pending edge when H is equal to 0.8D

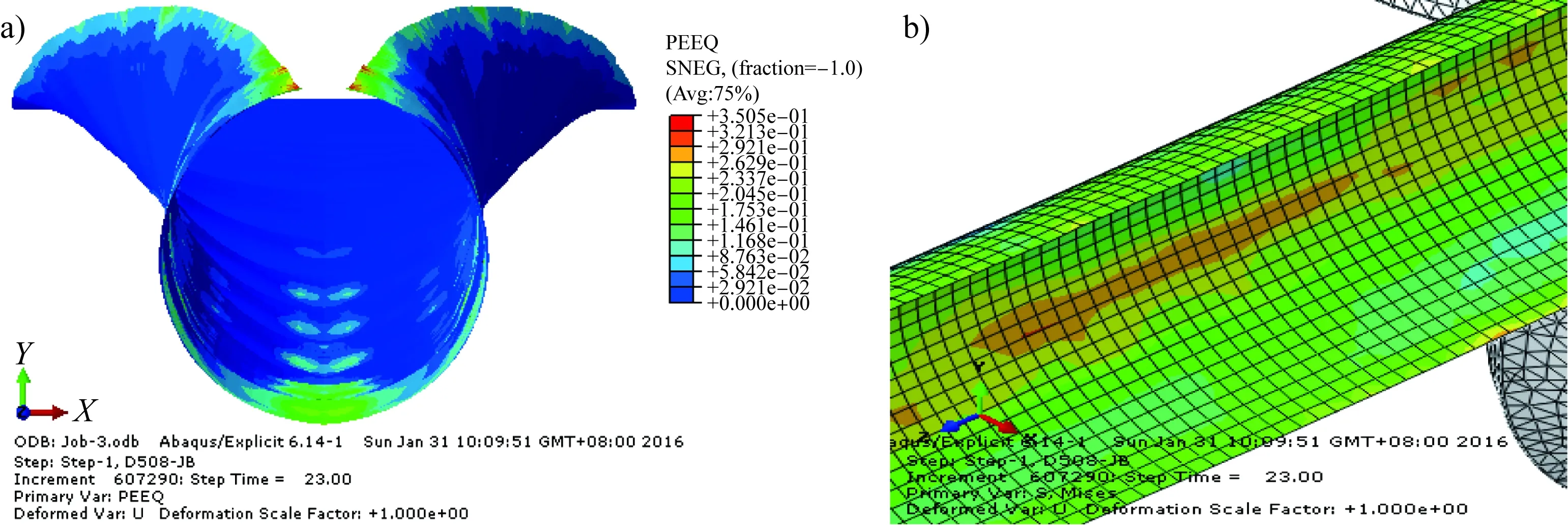
图8 H=1.0D时的(a)下山效果、等效塑性应变及(b)待焊边部形态Fig.8 (a)Downhill effect, equivalent plastic strain and (b) shape of the pending edge when H is equal to 1.0D

图9 H=1.2D时的(a)下山效果、等效塑性应变及(b)待焊边部形态Fig.9 (a)Downhill effect, equivalent plastic strain and (b) shape of the pending edge when H is equal to 1.2D

图10 管坯截面纵向应变方差的对比Fig.10 Variance of longitudinal strains at cross sections of pipes

对比以上结果可知，采用HFW660焊管机组生产φ508 mm×5.6 mm直缝焊管，当下山量H=1.0D时，其管坯的待焊边部较为平直，最大等效塑性应变最小，变形也最均匀，成形效果最好。

3.2.2 开口度的影响

由图1可见一个三点弯曲结构，它由约束成形底线的上辊和预成形段和线成形段机架两侧对称布置的一系列排辊及其底辊同时起作用。此结构效果明显，相比于其他辊式成形结构，其带钢两边被排辊约束，使得带钢边缘在成形过程中的回弹大大减小。因此，在轧制口径不一的焊管时，无需重新变更轧辊，改变排棍的位置即可。排辊的自由度较多，成形位置的开口度受排棍的棍位影响，通过调整开口度，可以改变板带在成形过程中的变形量分配并减少局部变形异常。在3.2.1节最优下山曲线的基础上，对原开口度(W)分别增大3%，减小3%、6%、9%进行计算，其开口度分别表示为W1、W2、W3、W4。4种开口度下管坯待焊边部形态如图11所示。

图11 不同开口度下待焊管坯边部形态Fig.11 Edge shape of the pipe blank with different roller positions to be welded

由图11可见，在开口度增大3%或减小9%时，焊接质量不佳，待焊管坯的边部不平整；当开口度减小3%或6%时，出精成形段后，待焊管坯的边部形态良好。图12为下山曲线和开口度优化前后成形效果的对比，可见边部褶皱消除，板带边部更加平直。

图12 下山曲线和开口度优化(a)前、(b)后管坯成形效果对比Fig.12 Comparison of edge shapes of pipe blank (a)before and (b)after optimization of roller data

“反弯”[7]现象出现在排棍成形段管坯的弯曲成形过程中，主要是由于某些位置轧辊棍位不对所致。正确辊位下断面弧线应呈外凸曲线，且圆心所标示方向在管坯中心线上，如图13所示，圆心所在位置在管坯的外面，局部弯曲方向与整体弯曲方向相反。生产中则轧辊的外部出现缺陷，并且产生多余的能耗及“包辛格效应”(引起材料强度下降)[10]，使管坯局部性能低于母材，导致产品不合格。

为了进一步了解开口度“反弯”情况，选择开口度W2、W3，此开口度下，管坯边部成形质量较好。在此，做如下要求：负值为反方向弯曲的圆弧的曲率，正值表示圆心在管坯内部的圆弧的曲率，负值曲率与反弯成正比。重点定位于轧制过程中带钢横截面的相对曲率，对板带横截面上负值曲率的区域进行积分，如图14所示。从图14中可以看出，在开口度W3下反弯弯曲量最小，在线成形三段处也出现了反弯，随着开口度的减小，反弯弯曲量均减小，且在大压下辊处出现明显的反弯。

4 结论

图13 带钢横截面反弯示意图Fig.13 Schematic diagram of reverse bending at cross section of strip steel图14 管坯负值曲率积分值 Fig.14 Negative curvature integral value of tube blank

(1)下山曲线及开口度对大径厚比焊管排辊成形中板带边浪缺陷、反弯及能耗有重要影响，模拟结果可指导优化辊位，预防产品缺陷。

(2)对φ508 mm×5.6 mm直缝焊管的排辊成形，选取下山曲线、开口度时，板带变形均匀、无边浪缺陷，且成形中反弯小，多余能耗及“包辛格效应”也小。