均布荷载下的抛物线形拱矢跨比的优化理论解
王康平 张 齐
(1.广东技术师范学院 天河学院, 广州 510540; 2.三峡大学 土木与建筑学院, 湖北 宜昌 443002)
拱结构被广泛应用于渡槽、涵洞、地下建筑、屋盖、桥梁等建筑物中.在拱轴形状的设计中,人们提出了“合理拱轴线”的概念,并导出了在均布荷载作用下的合理拱轴线方程[1-3],如图1所示.
y=4f(Lx-x2)/L2(1)
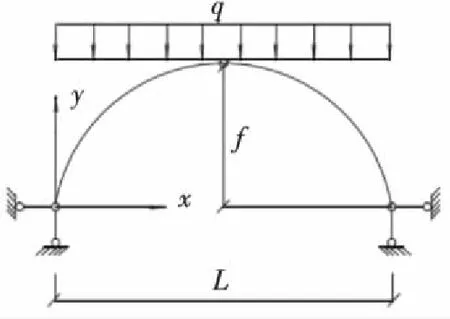
图1 均布荷载作用下的三铰拱示意图
这种合理拱轴线使拱圈的横截面上只受轴心压力的作用,从拱的受力性能来看,应该说是实现了拱轴形状的优化设计.但是拱轴力大小沿拱轴线分布为[3]
N=H/cosφ(2)

式中,H为拱的水平推力;φ为截面法线与水平坐标轴的夹角.
由式(2)与(3)可见,轴力与cosφ成反比,两脚处cosφ小,故轴力大;拱顶处cosφ大,故轴力小.若为了施工方便可仍采用等截面拱;若为了使拱截面应力大小沿拱轴线也均匀分布,常采用变截面高(截面宽b取为常量)[3]
h=h顶/cosφ(4)
但从经济性的角度来看,问题还需进一步研究.众所周知,确定拱形的一个重要参数是矢高,当荷载及跨长一定时,矢高的改变对拱的受力性能及工程造价都有很大影响.拱的矢跨比究竟取何值,才能使设计出的拱用料最省,造价最低?对这个问题,至今理论上没有确切的答案.文献[4]对这个问题进行了研究,在合理拱轴线与等截面的基础上,首先分析、建立了优化设计的数学模形,然后采用数值方法进行求解,导出了均布荷载作用下的最优矢跨比为1/3左右,并认为可取0.3~0.4.本文在拱轴线形与截面优化的基础上,用理论的方法得出均布荷载下的抛物线形变截面拱矢跨比的优化理论解;在拱轴线形优化的基础上,用理论的方法得出均布荷载下的抛物线形等截面拱矢跨比的优化理论解.
1 均布荷载下的抛物线形变截面拱矢跨比的优化理论解
由图1、式(2)与式(3)可见,矢高小的拱轴力大,要求截面大,但这时拱轴线较短;反之,矢高大的拱轴力小,要求截面小,但这时拱轴线较长.因此,必有一个最优的矢高使供体体积最小而使材料最省.下面就来求解这个最优的矢高.设拱体,弧长为S,体积为V,则
(5)
因为tanφ=y,所以
(6)

将公式(4)、(6)与(7)代入(5)得
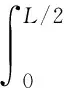
由公式(1)求出y′代入公式(8)解得

设拱体容许压应力为[σ],则bh顶=H/[σ],将公式(3)代入本公式后再代入公式(9)得
(10)

(11)

2 均布荷载下的抛物线形等截面拱矢跨比的优化理论解
若为了施工方便可采用等截面拱,其截面积
A=H/([σ]cosφ脚) (12)
拱脚处y′=4f/L,代入式(6)得

同理,仍有一个最优的矢高使供体体积最小而使材料最省.下面就来求解这个最优的矢高.拱体体积为
V=AS(14)
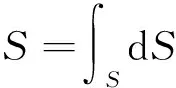
由公式(1)求出y′代入公式(7)再代入公式(15)得
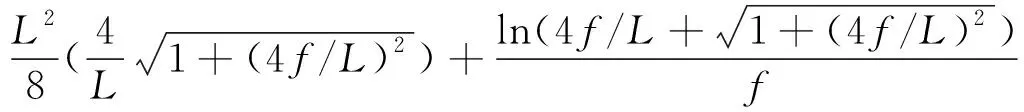
将公式(3)、(13)代入(12)再连同(16)代入(14)并整理得
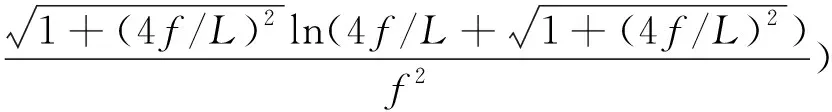
由dV/df=0解得最优矢跨比f/L=0.341 8,这时d2V/d2f>0,故有
(18)
综上所述,均布荷载下的抛物线形等截面拱矢跨比的优化理论解是0.341 8,其优化结果也是拱体体积最小.但从公式(11)与公式(18)可以看出,均布荷载下的抛物线形等截面拱最小体积比变截面的大35%.
3 均布荷载下的抛物线形拱矢跨比优化理论的应用范围
由图1可见,上述理论都是针对均布荷载下的抛物线形三铰拱的.那么,上述理论是否也适用于均布荷载下的抛物线形两铰拱或无铰拱呢?下面应用结构力学力法原理来回答这一问题.
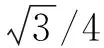
同理,把二次抛物线形无铰拱拱顶与两脚截面均变成铰也得二次抛物线形三铰拱作为力法求解的静定基,运用结构力学力法原理(只考虑弯曲变形的影响)也可求得拱顶与两脚处的多余约束力偶对均为零,即拱顶与两脚处均可改为铰,即无铰拱也变成了三铰拱.顺便指出,由于均布荷载下的悬索也呈抛物线形,且悬索只受轴心拉力,故均布荷载下的悬索与均布荷载作用下的抛物线形拱的不同只是拉压之别,故上述均布荷载作用下的抛物线形拱矢跨比的优化理论可精确运用于均布荷载下的悬索.综上所述,上述均布荷载作用下的抛物线形拱矢跨比的优化理论可精确运用于三铰拱与均布荷载下的悬索,也可近似运用于无铰拱与两铰拱.
4 结 论
2)均布荷载下的抛物线形等截面拱矢跨比的优化理论解是0.341 8,其优化结果也是拱体体积最小(见公式(18)).但从公式(11)与(18)可以看出,均布荷载下的抛物线形等截面拱最小体积比变截面的多35%.
3)均布荷载作用下的抛物线形拱矢跨比的优化理论可精确运用于三铰拱与均布荷载下的悬索,也可近似运用于无铰拱与两铰拱.

