骨料级配对水工全级配和湿筛混凝土拉伸断裂性能差异的影响
荆帅召 杨 鑫 周昌巧 刘 杰 徐 磊
(1.河海大学 水利水电学院, 南京 210098; 2. 重庆市水利电力建筑勘测设计研究院, 重庆 400020)
大体积水工混凝土结构多采用全级配(三级配或四级配)混凝土,与普通混凝土相比,其粗骨料粒径较大(如四级配水工混凝土的最大骨料粒径可达150mm).因而,工程实践中普遍采用湿筛混凝土标准试件代替全级配混凝土试件进行力学试验[1].由于湿筛混凝土的级配与骨料含量等与全级配混凝土有很大不同,因此,基于湿筛混凝土试验所得的力学指标与全级配混凝土的力学指标之间存在明显差异[2].
为了获取水工全级配混凝土的力学性能指标,相关学者针对这一差异已开展一些工作.始于美国垦务局开展的全级配混凝土力学试验,早期的研究工作主要侧重于分析水工全级配和湿筛混凝土抗压强度的区别[3].近年来,相关工作主要集中在国内.翟雪[4]和尹有君[5]对湿筛前后的混凝土试件进行了考虑冻融循环影响的劈裂抗拉试验,建立了全级配混凝土与湿筛混凝土劈裂抗拉强度的关系式.陈文耀和郑丹[6]从混凝土受拉受压的破坏机理出发分析了全级配混凝土与湿筛混凝土抗拉、抗压强度的差异原因.王刚[7]通过开展大坝及湿筛混凝土试件进行直拉断裂试验,对比研究了湿筛混凝土和大坝混凝土软化曲线的关系.周继凯等[8]结合小湾拱坝混凝土动态弯拉试验,对比分析了三级配混凝土与湿筛混凝土的动态弯拉力学特性关系.王怀亮等[9]分别对大坝原级配混凝土及其湿筛二级配混凝土进行双轴拉压和三轴拉压试验,比较分析了在不同受力情况下二者的强度和变形特性.李中田等[10]通过对碾压混凝土开展抗压强度、抗折强度、劈裂抗拉强度、静压弹性模量试验,对比分析了湿筛混凝土与全级配混凝土各项力学性能之间的关系.现阶段,相关研究主要采用物理试验方法,分析某一配合比下全级配与湿筛混凝土力学性能指标的差异程度.由于不同的全级配混凝土通常有着不同的宏观强度、骨料含量和骨料级配,故上述力学性能的差异亦随研究对象的不同而发生改变.
此外,已有研究表明混凝土的细观随机结构对其宏观力学性能有着很大的影响[11-12],故而在全级配和湿筛混凝土力学性能差异的研究过程中应尽可能消除细观随机结构的影响,但在以往的物理试验研究中,试件数量通常较少,难以获取具有统计意义的分析结果.另一方面,细观有限元分析已在混凝土力学性能研究中得到越来越广泛的应用[11-12].相对于物理试验方法,混凝土细观有限元分析耗时少,费用低,不受试件尺寸的影响,分析结果受到的干扰少,且可同时在宏观和细观两个尺度上开展对比分析,可作为物理试验方法的有力补充.鉴于此,论文研究采用细观有限元分析与Monte Carlo模拟相结合的方法,在分析不同骨料级配水工全级配和湿筛混凝土拉伸断裂性能差异的基础上,重点探究上述差异随骨料级配的变化规律.研究成果不仅可揭示骨料级配对水工全级配和湿筛混凝土拉伸断裂性能差异的影响规律,亦可为基于湿筛混凝土拉伸断裂性能指标(拉伸弹性模量、峰值抗拉强度、峰值拉伸应变及断裂能)推求水工全级配混凝土拉伸断裂性能指标提供参考,具有重要的学术意义和工程应用价值.
1 混凝土细观有限元计算模型
在细观尺度上,将水工全级配与湿筛混凝土视为由粗骨料、砂浆及二者之间的界面过渡区构成的三相随机复合材料.在建立全级配与湿筛混凝土细观有限元计算模型的过程中,所涉及的关键技术问题主要包括材料细观结构的生成、细观有限元网格的剖分、细观本构模型及力学参数的确定、荷载与边界条件的施加以及数值求解的策略等,简述如下.
在给定骨料含量和骨料级配的基础上,采用基于“take-and-place”的参数化建模方法实现水工全级配和湿筛混凝土细观随机结构的自动生成.为分析骨料级配的影响,分别建立了三级配和四级配的全级配混凝土数值试件及其相应的湿筛混凝土试件.对于三级配试件(平面尺寸为300 mm×300 mm),平面骨料含量取为50%,骨料级配取为小骨料∶中骨料∶大骨料=30∶30∶40,由此,可推求与三级配试件对应的湿筛混凝土试件(平面尺寸为150 mm×150 mm)的骨料含量与级配.对于四级配试件(平面尺寸为450 mm×450 mm),平面骨料含量亦取为50%,骨料级配取为小骨料∶中骨料∶大骨料∶特大骨料=25∶25∶20∶30,同样,可据此推求与四级配试件对应的湿筛混凝土试件(平面尺寸为150 mm×150 mm)的骨料含量与级配.图1给出了所生成的典型四级配、三级配及其湿筛试件的细观结构图,图中多边形代表骨料.
对于确定了细观结构的混凝土试件,需对其进行网格剖分,为此,利用ABAQUS的前处理模块,并通过MATLAB和PYTHON混合编程,实现了混凝土细观有限元网格的自动剖分.图2给出了图1(b)、图1(d)所示试件的有限元网格剖分图,从图中可以看出,细观有限元网格对具有复杂形状的骨料边界实现了精确模拟.需要说明的是,粗骨料和砂浆之间的界面过渡区是在有限元网格剖分过程中引入的,其厚度取为100 μm.
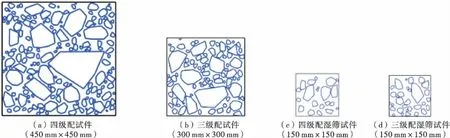
图1 全级配和湿筛混凝土试件的细观结构

图2 细观有限元网格剖分
已有的研究成果表明,界面过渡区可被视为力学弱面,混凝土的拉伸断裂首先是在界面过渡区处产生微裂缝,进而扩展至砂浆,并最终通过微裂缝集聚产生宏观断裂面,在这一过程中,骨料通常不会产生损伤破坏[13].因此,在所建立的细观有限元计算模型中,采用线弹性本构模型模拟骨料的力学行为,对于砂浆和界面过渡区,则采用ABAQUS中的塑性损伤模型进行模拟.为了体现界面过渡区的“弱面效应”,将其力学参数取为砂浆力学参数的75%[14].此外,考虑到大骨料(粒径≥40 mm)周围的界面过渡区相对于小骨料(5 mm≤粒径<40 mm)周围的界面过渡区更为软弱,模拟中将二者力学参数的比值取为0.8[15].为了使得所采用的细观力学参数更为符合实际,依据《混凝土结构设计规范(GB50010-2010)》[16]中给出的C20混凝土单轴受拉应力应变曲线,采用异步粒子群优化算法[17]对砂浆和界面过渡区的主要力学参数(弹性模量、峰值抗拉强度、断裂能)进行了反演,细观有限元分析中采用的主要力学参数见表1.

表1 细观力学参数
为研究水工全级配和湿筛混凝土的拉伸断裂行为,对所建立的混凝土细观有限元数值试件进行单轴拉伸模拟,模拟中对模型左侧边界施加零位移约束,在模型右侧施加均布水平位移边界条件,最大水平位移为试件边长的0.006倍(即相当于600微应变).由于混凝土断裂过程中会出现明显的应变软化现象,故为了避免在隐式有限元分析中经常出现的计算不收敛现象,分析采用ABAQUS/EXPLICIT显式求解器进行计算,通过试算,位移加载速率取为5 mm/s,计算结果表明,在此加载速率下可实现准静态断裂过程的模拟.
2 Monte Carlo模拟
在骨料含量、级配、细观本构模型、力学参数、边界条件与荷载等其它条件均相同的前提下,具有不同随机结构的混凝土细观有限元数值试件一般有着相异的细观断裂机制与宏观应力应变特性.为了消除细观结构随机性对差异分析结果的影响,论文研究中开展了Monte Carlo模拟,即对于每一类分析对象(三级配混凝土、三级配湿筛混凝土、四级配混凝土、四级配湿筛混凝土),均分别生成M个具有不同随机结构的细观有限元数值试件,进而在相同条件下对这M个试件进行数值分析,并以宏观拉伸断裂性能指标的统计均值描述这一类混凝土的拉伸断裂性能.
依据Monte Carlo随机试验的基本原理,M(即样本的数量)需要足够大以保证试验结果达到统计收敛.在本文中,通过分析各类混凝土宏观拉伸断裂性能指标的统计均值随样本数量增加的变化趋势,发现当样本数量超过30时,上述指标的统计均值基本上保持不变(达到了统计收敛),因此,在论文工作中,M取为30,即共开展4×30=120次细观有限元分析.
对于任一细观有限元分析,均需依据细观分析结果计算宏观拉伸断裂性能指标的量值(拉伸弹性模量Et、峰值抗拉强度ft、峰值拉伸应变εt及断裂能Gf),其中,峰值抗拉强度为模型右侧结点总结点反力的峰值与模型试件边长的比值,而峰值拉伸应变为达到峰值抗拉强度时的水平位移与模型试件边长的比值,考虑到达到峰值抗拉强度前宏观应力应变曲线总体可视为线性关系,故拉伸弹性模量为上述二者的比值,此外,依据分析所得的拉伸应力位移曲线,可计算出断裂能.
3 成果分析
在上述基础上,针对上文所述的各类混凝土开展了大量细观有限元分析,图3分别给出了各种混凝土试件宏观应力应变曲线及其平均曲线.
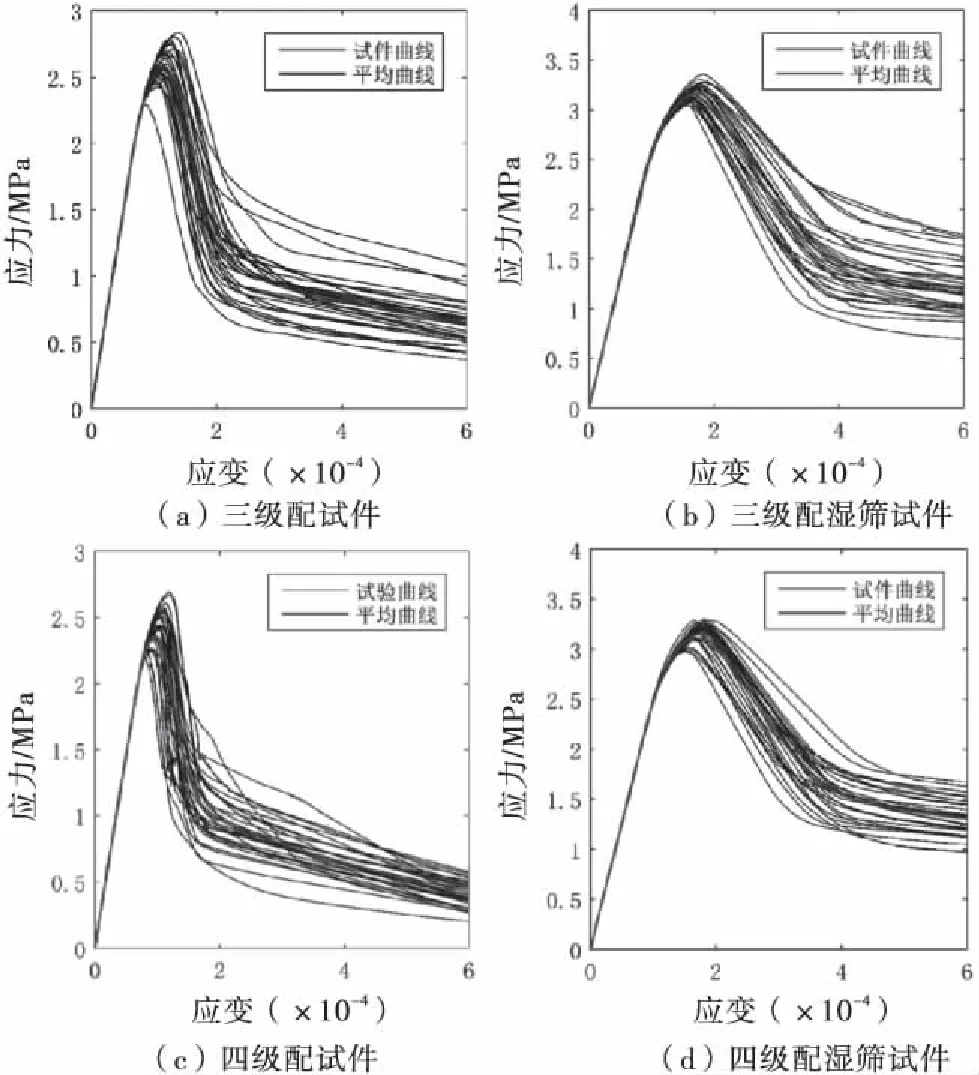
图3 宏观应力应变曲线
从图3可以看出,对于同一类混凝土,各试件应力应变曲线在峰前基本保持一致,且总体呈现出线性关系,但在峰后软化段,应力应变曲线有着明显的离散性,表明细观结构对于宏观软化阶段的影响较大,这也验证了在研究中实施Monte Carlo模拟的必要性.另一方面,由图3(a)~3(d)可以看出,受到骨料含量与级配变化的影响,虽然全级配混凝土与其湿筛混凝土有着不同的宏观拉伸应力应变曲线,但这种差异主要体现在量值上,曲线仍具有类似形状和变化趋势(准脆性断裂过程).
图4给出了三级配混凝土ft与Gf的均值与样本数量N之间的关系曲线.从图4中可以看出,随着样本数量的逐渐增大,三级配混凝土ft与Gf的均值均逐渐趋于稳定,当N超过20时,ft与Gf的均值基本上保持不变.三级配混凝土的其它参数以及其它3类混凝土的参数的均值与样本数量之间关系亦类似,限于篇幅,不再给出.如前所述,本文研究中取样本数量为30,可保证分析结果具有统计代表性.表2列出了各类混凝土宏观拉伸断裂参数的统计均值与相应的比值.
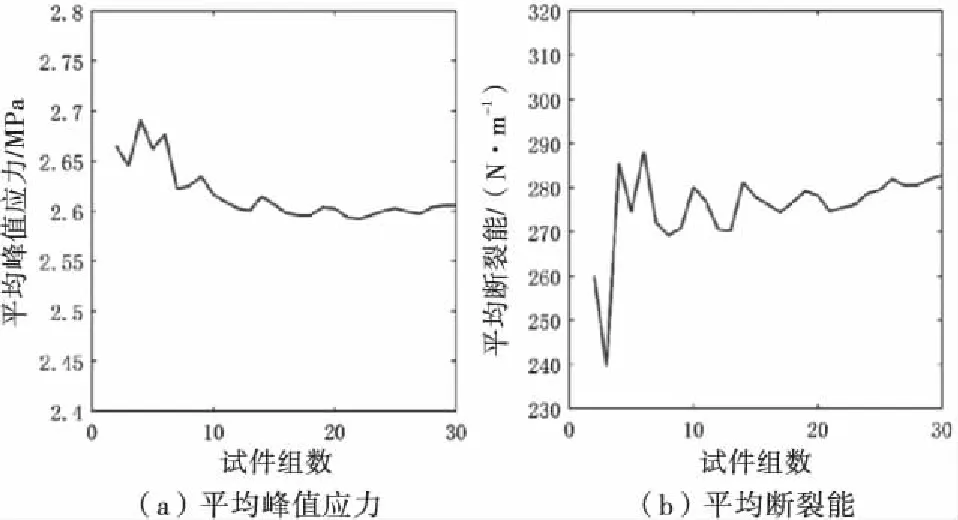
图4 统计均值与样本数量的关系曲线
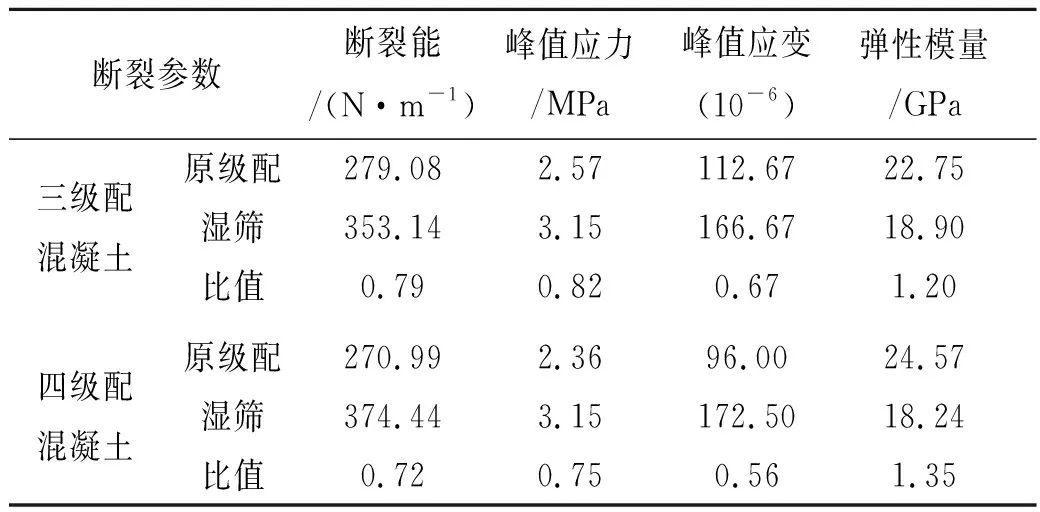
断裂参数断裂能/(N·m-1)峰值应力/MPa峰值应变(10-6)弹性模量/GPa三级配混凝土原级配279.082.57112.6722.75湿筛353.143.15166.6718.90比值0.790.820.671.20四级配混凝土原级配270.992.3696.0024.57湿筛374.443.15172.5018.24比值0.720.750.561.35
从表2可以看出,与湿筛混凝土相比,原级配(三级配或四级配)混凝土的拉伸弹性模量相对较大,其主要原因是原级配混凝土中的骨料含量较高;而对于具有相同骨料含量的三级配和四级配混凝土,后者的拉伸弹性模量较大,这主要是由于后者骨料级配中的大骨料占比高;相对于三级配湿筛混凝土,四级配湿筛混凝土的拉伸弹性模量略小,主要原因是其骨料含量略低;对于原级配与湿筛混凝土拉伸弹性模量的比值,三级配低于四级配,考虑二者的湿筛混凝土具有相近的拉伸弹性模量,故上述比值的变化主要是由于四级配中大骨料占比高的原因.换言之,随着骨料粒径的增大和大骨料占比的提高,全级配与湿筛混凝土拉伸弹性模量的差异趋于增大.
对于峰值抗拉强度,与湿筛混凝土相比,原级配混凝土的峰值抗拉强度明显降低,这主要是由于原级配混凝土中大骨料的存在,而三级配混凝土的抗拉强度大于四级配混凝土的主要原因亦可归结于此;虽然四级配湿筛混凝土的骨料含量低于三级配湿筛混凝土,但二者的抗拉强度基本相同,这表明相对于骨料含量,骨料粒径对混凝土抗拉强度的影响更为明显;对于原级配与湿筛混凝土抗拉强度的比值,三级配大于四级配,原因主要在于四级配混凝土中含有粒径更大的骨料以及大骨料占比的提高.也就是说,随着骨料粒径的增大和大骨料占比的提高,全级配与湿筛混凝土峰值抗拉强度的差异亦趋于增大.
由于原级配混凝土相较于湿筛混凝土具有较大的拉伸弹性模量和较小的峰值抗拉强度,故其峰值拉伸应变较湿筛混凝土更小;从表2中亦可看出,对于原级配与湿筛混凝土峰值拉伸应变的比值,三级配大于四级配,这与骨料级配变化所导致的拉伸弹性模量与峰值抗拉强度差异的变化规律是一致的,即随着骨料粒径的增大和大骨料占比的提高,全级配与湿筛混凝土峰值拉伸应变的差异趋于增大.
与湿筛混凝土相比,原级配混凝土的断裂能明显降低,其原因主要在于原级配混凝土中存在大骨料及骨料含量占比的提高;与三级配湿筛混凝土相比,四级配湿筛混凝土的断裂能相对较大,这是由于其骨料含量相对较小;而与三级配混凝土相比,四级配混凝土的断裂能相对较小,这表明在骨料含量相同的条件下,大骨料占比高将导致断裂能的降低;在上述因素的综合影响下,对于原级配与湿筛混凝土断裂能的比值,三级配大于四级配,即随着骨料粒径的增大和大骨料占比的提高,全级配与湿筛混凝土断裂能的差异趋于增大.
4 结 语
为揭示骨料级配的变化对水工全级配和湿筛混凝土拉伸断裂性能差异的影响,论文综合采用混凝土细观有限元分析方法与Monte Carlo模拟方法,针对不同骨料级配的原级配及其湿筛混凝土拉伸断裂性能的差异进行分析,并在此基础上重点讨论了由于骨料级配的不同所导致的断裂性能差异的变化.结果表明,骨料级配的变化对全级配与湿筛混凝土的拉伸断裂性能差异有着较为明显的影响,总体而言,随着骨料粒径的增大和大骨料占比的提高,全级配与湿筛混凝土拉伸断裂性能指标间的差异均趋于增大;针对具体的宏观拉伸断裂性能指标,随着骨料粒径的增大和大骨料占比的提高,拉伸弹性模量的比值(大于1)增大,峰值抗拉强度、峰值拉伸应变及断裂能的比值(小于1)减小.

