基于损伤理论的混凝土裂缝扩展研究

陈 军 王向东 韩金启

(河海大学 力学与材料学院， 南京 211100)

混凝土在浇筑成型过程中不可避免的会有初始损伤，初始损伤在外载的作用下会不断的演化发展，产生微裂纹区直至形成宏观裂缝，因此混凝土的破坏过程实质上是损伤产生、发展、形成宏观裂缝、裂缝扩展、直至结构破坏的过程．损伤力学和断裂力学都属于破坏力学范畴，两者各有不同但又相互关联，损伤力学主要研究材料内的微缺陷和微裂纹，即在变形过程中损伤产生、演化发展的过程及其对材料力学性能的影响[1]；断裂力学则研究宏观裂纹尖端的应力、应变场、应力强度因子、能量释放率和断裂能等，从而建立起宏观裂纹起裂、稳定扩展和失稳扩展的判据[2]，进而进行裂缝稳定性研究．所以要真正了解混凝土材料的裂纹产生、发展的过程，就需把损伤力学和断裂力学方法结合起来，用损伤与断裂耦合的分析方法来研究混凝土的破坏，这样才可以更好的反应出材料破坏的实际过程[2]．

为了研究带裂缝结构的安全性，经过多年的研究，学者们[3-5]引进了新的断裂参量，如应力强度因子K和能量释放率G等，建立了应力强度因子K判据和能量释放率G判据等，用于分析裂缝的稳定性．而裂缝之所以扩展是缝端损伤积累的结果，为了描述混凝土带缝结构裂缝开始扩展的原因，本文从损伤力学入手研究缝端的损伤区域及其演化规律．为了描述材料损伤特性，学者们建立了一些损伤模型．经典的损伤模型有Loland模型和Marzars模型，此外还有Krajcinovic损伤模型和徐变损伤模型[6]等．其中，Loland模型最具有代表性，因为其考虑了材料的初始损伤，该模型所计算得出的损伤状况与试验数据符合较好[7]．所以，其应用也比较多，故本文在研究混凝裂缝的扩展中采用Loland模型．推导损伤区域的表达式，建立损伤判据和损伤半径判据，将该研究结果用于分析带缝结构，如混凝土梁和带缝混凝土重力坝裂缝发生扩展的原因，以便于混凝土结构的安全性分析．

1 基于Loland损伤模型的双D判据

材料变形往往与损伤联系在一起，物体内的损伤是一种连续的场变量，而描述这种材料损伤状态的场变量就称为损伤变量D，本文所采用的Loland损伤演化方程为：

(1)

演变方程中，C1、C2和β是材料常数．由于ε=εf时σ=σf，且dσ/dε=0并考虑到ε=εu时D为1，所以可以得到：

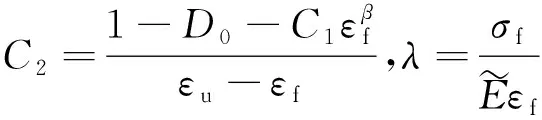
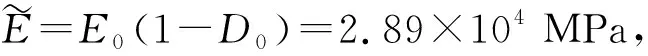
D(ε)=

对于Loland损伤模型，考虑到其建立在单轴均匀应力场的条件下，所以图1中应变εc对应起裂损伤Dini，随着损伤的累积，当应变达到图中的失稳应变εun时，损伤失稳发展，对应失稳损伤Dun．

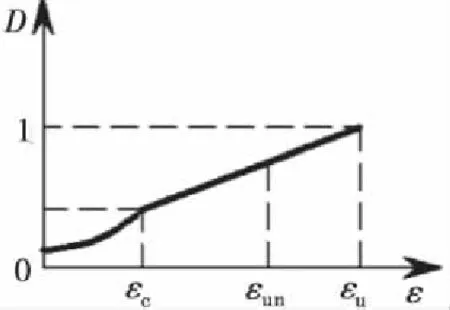
图1 模型

建立描述裂缝尖端损伤发展的双D损伤判据：当裂缝尖端的损伤小于起裂损伤Dini时，缝端损伤处于产生阶段，微裂纹区形成；当裂缝尖端的损伤介于起裂损伤Dini和失稳损伤Dun之间时，缝端损伤处于稳定积累阶段，微裂纹区发展；当裂缝尖端的损伤大于Dun时，缝端损伤处于快速失稳发展阶段，微裂纹区发展为宏观裂缝．所以描述裂缝尖端损伤发展的判据可以表示为：

2 基于Loland损伤模型Ⅰ-Ⅱ复合型裂缝损伤断裂区

如图2所示，混凝土中具有与x轴成夹角α的斜裂纹，并在边界处受到沿x轴方向的拉应力σ作用，则图中的裂缝即为Ⅰ-Ⅱ复合型裂缝，由线弹性断裂力学原理，Ⅰ-Ⅱ复合型裂缝缝端应力场可由叠加原理得：

(4)

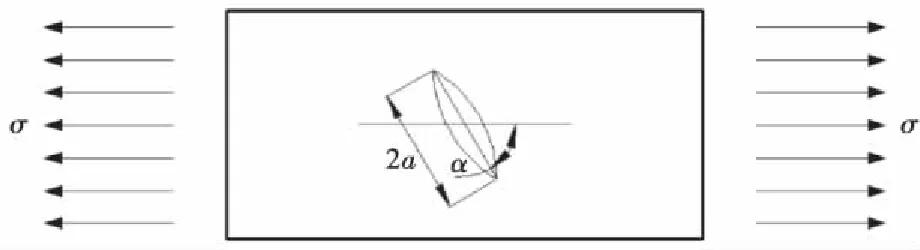
图2 中心斜裂纹单向拉伸

由σ主应力和分应力的关系，可以推出主应力满足：

由于混凝土为脆性材料，抗压不抗拉所以认为混凝土破坏的主要原因是拉应变导致，损伤主要由拉应变引起．由应力应变关系可以由式(5)推导出最大拉应变为：

(6)

式中，系数

(7)

将式(6)代入式(1)整理得

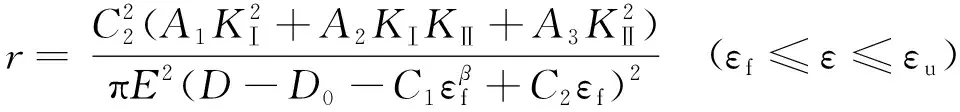
又有

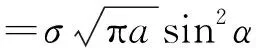
式中，KⅠ和KⅡ分别为第一应力强度因子和第二应力强度因子，σ为拉应力，α为斜裂纹的倾角．并将式(9)代入式(8)中整理得到：

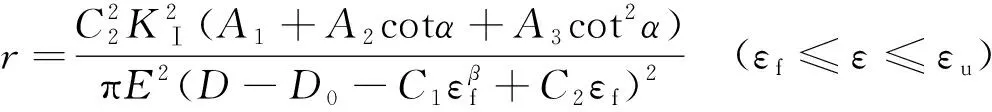
由式(10)计算出当D=1，角θ=0时，KⅠ和KⅡ的比值不同时的损伤半径r的数值．见表1．

表1 各组Ⅰ-Ⅱ复合型裂缝损伤半径计算表(D=1)

当取角θ=0度时，由损伤半径的公式(10)可得Ⅰ-Ⅱ复合型裂缝损伤发展演化的过程如图3所示．对应于起裂损伤Dini，裂缝尖端对应着一个起裂时的损伤半径rini，当裂缝尖端的损伤半径小于起裂损伤rini时，缝端损伤处于产生阶段，微裂纹区形成；对应失稳损伤Dun，则裂缝尖端对应着一个失稳时的损伤半径run，当裂缝尖端的损伤介于起裂损伤半径rini和失稳损伤run之间时，缝端损伤处于稳定积累阶段，微裂纹区发展；当裂缝尖端的损伤大于run时，缝端损伤处于快速失稳发展阶段，微裂纹区发展为宏观裂缝．

图3 Ⅰ-Ⅱ复合型裂缝损伤断裂区域

则对应于双D损伤发展判据，也可以表述为双r损伤判据：

3 Ⅰ-Ⅱ复合型裂缝损伤断裂区的数值分析

Ⅰ-Ⅱ复合型裂缝在诸多复合型裂缝中最为常见，也是人们研究最多的一类复合型裂缝问题．通过探索研究发现，Acapinter在1988年根据Losipescu试件改进而成的反对称加载的单边裂缝四点剪切样是较为理想的试件[9]．河海大学断裂力学课题组进行的系列断裂试验[10]中的Ⅰ-Ⅱ复合型也采用单边裂缝四点剪切式样进行试验，如图4所示．其中b=h=100 mm，S=3S′=180 mm，初始裂缝长度a0=50 mm．f表示裂缝的位置．

图4 Ⅰ-Ⅱ复合型裂缝断裂试验试件尺寸

根据试验数据进行了3组拉剪断裂模型的数据计算，给出其中一组f为10 mm模型的损伤数值计算图，如图5～6所示．相应的结果见表2．

图5 起裂荷载下损伤等值线

图6 失稳荷载下损伤等值线

组号f/mm起裂荷载/kN失稳荷载/kNKⅠ/KⅡ起裂损伤Dini失稳损伤Dum起裂半径/mm失稳半径/mm理论计算失稳半径/mm140436867203.33410.54500.72886.5105.6545.435220582489601.37450.56820.73465.5844.71794.3743106734103600.64960.66110.76955.1174.3363.861

由数值计算得出的失稳半径与理论计算得到的的损伤失稳半径非常相近，并且其变化趋势一致，由此验证本文方法的合理性．

4 重力坝模型损伤区计算分析

混凝土坝体的裂缝的出现是由于损伤的不断演化发展导致的，因此，若能够在混凝土的裂缝出现以前就能够确定损伤区的范围，就可以提前对坝体进行预加固，可以预防裂缝的出现，比裂缝出现再进行加固更安全也更经济．若已经产生了裂缝，可以将裂缝尖端的损伤区大小计算出，然后对损伤区进行加固处理，就可以防止裂缝的发展．

本文选国外某重力坝为计算对象：坝高103 m、坝顶宽度14.8 m、坝段厚16 m、坝底宽度70 m．重力坝的坝体混凝土材料弹性模量E=31.027 GPa，泊松比v=0.15，密度为ρ=2 463 kg/m3，动态拉伸屈服强度σd=2.9 MPa，抗压强度σc=24.1 MPa，断裂能G=250 N/m．重力坝模型如图7所示．

图7 重力坝坝段轮廓

由文献[11]分析结果得知，坝体截面突变处易产生裂缝．故在坝体截面突变处预制一个长度为6 m的裂缝，利用有限元软件ANSYS先建立平面模型，裂缝尖端离截面突变处距离为6 m，在裂缝尖端处设置奇异性，所以网格划分不再是规则的，如图8所示．

图8 带裂缝重力坝三维模型 图9 裂缝尖端最大主应变云图

取模型中间一坝段分析，用有限元软件自带的应力强度因子方法，求得KⅠ=0.320 15 (MN·m-3/2)、KⅡ=0.564 47 ×10-4(MN·m-3/2)，因此可以知道裂缝类型为Ⅰ-Ⅱ复合型裂缝．当重力坝的背侧水位到达坝顶时，计算出此时裂缝尖端的最大主应变云图如图9所示．

经过试算，得出当重力坝上游水位为98.2 m的时候，计算得到裂缝尖端的应变为ε=183 με，此时对应的损伤即为起裂损伤如图10所示，当h≤98.2 m时，此时缝端的损伤0rini；当98.2 m100 m时，此时缝端的损伤D>Dun，损伤半径r

图10 起裂荷载下裂缝尖端损伤图

图11 失稳荷载下裂缝尖端损伤图

工程中可以通过在混凝土内部埋设应变传感器，观测应变的变化，并根据公式(3)及公式(10)，通过应变可以得知损伤以及损伤区域的大小，并结合双D损伤判据和双r损伤判据来判断结构中裂缝的安全性，在工程应用中具有一定的实际意义．

5 结 论

1)推导了Ⅰ-Ⅱ复合型裂缝尖端区域的损伤断裂区域方程，并提出双D损伤判据和双r损伤半径判据．

2)利用有限元软件建立并模拟该复合型裂缝验证理论计算结果的准确性．

3)将损伤区理论应用在在工程实例中，计算出带裂缝重力坝的起裂损伤区以及失稳损伤区，分析了坝体裂缝在相应荷载作用下的安全性．