非平稳地震动场的随机函数模拟

阮鑫鑫 刘子心 刘章军，2

(1. 三峡大学 土木与建筑学院， 湖北 宜昌 443002； 2. 防灾减灾湖北省重点实验室(三峡大学)， 湖北 宜昌 443002)

地震灾害作用具有显著的随机动力特性和空间变异特性，一般用时间变量和空间变量的随机场来描述，即所谓的时空随机场[1]．对于复杂工程结构(如大跨桥梁、大坝等)，地震灾害作用的空间变异特性不可忽视[2]．因此，在复杂工程结构的非线性随机地震反应分析中，时空随机场的模拟至关重要．目前，蒙特卡罗随机模拟方法在工程实际中受到越来越多学者的关注和重视，其中谱表示法由于其精度高和易于实现而被广泛使用．40多年来，Yang[3]、Shinozuka[4]、Deodatis[5]等在谱表示的理论及应用方面开展了卓有成效的工作，使得谱表示方法臻于完善．

然而，采用传统的谱表示方法模拟地震动时空随机场时，往往需要高达数万个随机变量来表达地震动时空随机场，这为复杂工程结构的非线性随机地震反应分析与抗震可靠度计算带来巨大挑战[6]．因此，如何有效地降低谱表示方法随机变量的数量已成为近年来的研究热点．为此，陈建兵等[7]发展了随机过程的随机谐和函数表达，通过少量的随机谐和分量即可获取精确的目标功率谱．随后，刘章军等[8-10]提出了一种随机函数降维方法，实现了仅用1-2个基本随机变量即可精细地模拟一维单变量平稳和非平稳随机过程以及多变量平稳随机过程．

为此，本文将在地震动时空随机场的原始谱表示基础上，引入随机函数的约束形式，实现2D-1V地震动时空随机场的降维模拟，并结合FFT算法极大地提高模拟的计算效率，从而为地震动时空随机场模拟提供一种更为精细有效的方法．

1 2D-1V时空随机场的谱表示

设f0(x，t)是一个零均值、实值的2D-1V时空随机场，在时间域上是平稳或非平稳，在空间域上是均匀或非均匀，单边的频率-波数谱Gf0(x，t；κ，ω)=2Sf0(x，t；κ，ω)，其中Sf0(x，t；κ，ω)为双边的频率-波数谱．于是，2D-1V时空随机场f0(x，t)则可表达为如式(1)的积分形式[4]：

sin(κx+ωt)dVx，t(κ，ω) (1)

式中，Ux，t(κ，ω)和Vx，t(κ，ω)是定义在-∞<κ<∞和0<ω<∞上的两个实值正交过程，其增量dUx，t(κ，ω)和dVx，t(κ，ω)满足如式(2)的条件：

(2)

显然，当dUx，t(κ，ω)和dVx，t(κ，ω)均与空间无关时，式(1)即为非平稳均匀的2D-1V时空随机场的谱表示．

进一步，将式(1)近似写为如下的有限级数形式：

sin(κmx+ωnt)ΔVx，t(κm，ωn)]+

[cos(-κmx+ωnt)ΔUx，t(-κm，ωn)+

sin(-κmx+ωnt)ΔVx，t(-κm，ωn)]} (3)

其中

κm=(m-0.5)Δκ，ωn=(n-0.5)Δω(4)

式中，M和N分别为波数和频率的截断项数，Δκ为波数步长，Δω为频率步长．Δκ与Δω应足够小，以便保证式(3)能近似代替式(1)．

在式(3)中，若定义正交增量为

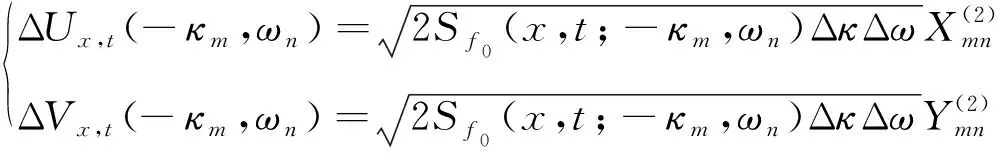
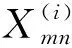
将式(5)代入式(3)中，得到

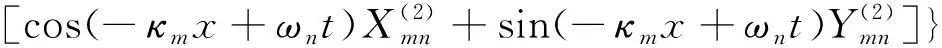
式(7)即为2D-1V时空随机场的基于正交随机变量的谱表示，也就是所谓的原始谱表示．

(8)

于是，将式(8)代入式(7)中，即可得到2D-1V时空随机场模拟的基于随机相位角的传统谱表示[5]．

2 2D-1V时空随机场的随机函数模拟

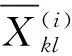
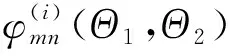
需要指出的是，式(10)可以采用快速傅里叶变换(FFT)来提高计算效率；同时，基本随机变量Θ1和Θ2是采用数论方法[11]来生成代表性点集，而非蒙特卡罗方法生成．

在利用式(10)模拟2D-1V时空随机场时，首先需要给出2D-1V时空随机场的频率-波数谱Sf0(x，t；κ，ω)的表达式，对于非平稳均匀的2D-1V时空随机场的频率-波数谱应为Sf0(t；κ，ω)．

3 地震动场模型

为了模拟非平稳均匀地震动随机场，首先需要给出相应的平稳均匀地震动随机场的频率-波数谱．对于平稳均匀地震动随机场的频率-波数谱S(κ，ω)，可由平稳地震动过程的自功率谱S(ω)与地震动场的空间相干函数的傅里叶变换之乘积得到[2]：

(12)

在本文中，地震动场的空间相干函数采用考虑行波效应的Luco-Wong模型[2]

γ(ξ，ω)=e-α2ω2ξ2e-iωξ/νapp(13)

将式(13)代入式(12)，得到频率-波数谱S(κ，ω)的表达式为[2]

(14)

式中，参数α=0.147，视波速νapp=1 000 m/s．

对于平稳地震动加速度过程的自功率谱S(ω)，本文采用Kanai-Tajimi谱[2]：

(15)

式中，场地卓越圆频率ωg=5π rad/s，阻尼比ζg=0.6，谱强度因子S0=44.29 cm2/s3．

为了反映地震动过程的时-频非平稳性，本文采用如下的时-频调制函数[9]：

其中

式中，参数b=a+0.001，c=0.005．这样，上述时-频调制函数中只有一个独立参数a，本文取a=0.2s-1．

于是，非平稳均匀地震动时空随机场的频率-波数谱的表达式为：

Sf0(t；κ，ω)=A2(t，ω)S(κ，ω) (17)

4 数值算例

现在，在水平地面上沿x方向选择2 048个作用点，且两两间距为10 m，地震动有效持时20 s．为了模拟非平稳均匀地震动时空随机场，采用如下计算参数：截断波数κu=π/10 rad·m-1，截断频率ωu=50π rad·s-1，波数离散点数M=512，频率离散点数N=1 024．为利用FFT技术，本文使用Peng等[12]建议的方法，将非平稳随机地震动场分解为6个强度调制的随机地震动场之和．选择FFT的波数和频率变换点数为2M和2N，因此对应空间间隔Δx=10.0 m，时间间隔Δt=0.02 s，场的空间尺度L=20 480 m，地震动模拟持时T=81.92 s．虽然地震动的模拟持时大于有效持时，但这并不会增加过多的计算工作量，因为本文方法的模拟效率足够高．在确定模拟参数后，利用数论方法选取基本随机变量Θ1和Θ2的代表性点集，本文选取代表性点的数量nsel=377，再利用式(10)即可生成非平稳均匀地震动时空随机场的代表性时程．

为分析方便，选择3个位置处的地震动随机过程的代表性时程进行分析．其中，位置1为第201点处，即x1=2 000 m；位置2为第205点处，即x2=2 040 m；位置3为第211点处，即x3=2 100 m．图1为本文方法生成的3个位置处的地震动加速度代表性时程，可见代表性时程在时间和频率上具有显著的非平稳特性．此外，3个位置处的代表性时程在波形变化方面也具有一定的相似性，这反映了3个点之间的空间相干效应．

(a)位置1处;(b)位置2处;(c)位置3处图1 非平稳地震动加速度代表性时程

图2为本文方法生成的位置1处377条地震动加速度代表性时程的均值及标准差与目标值的比较．从图中可知，均值和标准差的模拟值与目标值均拟合很好．对于位置2和3处的地震动加速度代表性时程的均值和标准差，也能得到类似的结果，这初步验证了本文方法的有效性．

图2 位置1处的377条非平稳地震动加速度代表性时程的均值和标准差

图3为本文方法生成的377条地震动加速度代表性时程在位置1、2、3处的自相关函数及互相关函数与目标值的比较，可见3个位置处的自相关与互相关函数的模拟值均与目标值拟合一致，这进一步验证了本文方法的有效性．

图3 在t=5 s时3点的相关函数模拟值与目标值的比较

为了进一步说明本文方法的优越性，在模拟效率和精度方面与传统的谱表示方法进行比较．在模拟效率方面，模拟2 048个位置点处随机过程的全部样本时，本文方法的耗时为673 s，传统谱表示方法的耗时为664 s．在模拟精度方面，本文方法的均值相对误差和标准差相对误差分别为2.55%和2.83%，而传统谱表示方法的均值相对误差和标准差相对误差分别为4.10%和2.96%．其中，均值和标准差的相对误差定义见文献[8]，且最终的相对误差均取3个位置处相对误差的平均值．由此可见，本文方法的模拟效率与传统方法大致相当，但本文方法的模拟精度更高，体现了优越性．

5 结 论

本文建议了一种基于随机函数的时空随机场降维模拟方法．该方法是在基于正交随机变量的谱表示上，通过将谱表示中的正交随机变量均定义为两个基本随机变量的正交函数形式，从而实现地震动时空随机场的降维模拟．数值算例表明，本文方法的模拟效率与传统方法大致相当，但本文方法的精度更高．同时，由于本文方法仅需2个基本随机变量表达地震动随机场，从而可利用数论方法生成具有完备概率的代表性样本集，这为应用概率密度演化理论进行结构的随机地震反应和抗震可靠度分析奠定了基础．