圆柱的变化

刘善娜（特级教师）

【教学内容】

学完人教版六年级下册《圆柱的表面积》《圆柱的体积》之后。

【教学目标】

1.通过画圆柱的切割图，让学生进一步理解“截面”的含义，培养其空间能力。

2.通过画圆柱的切割图，进一步优化表面积、体积问题的解决策略。

3.通过图形的动态变形，让学生感受圆柱表面积与体积的变化，在解决问题中发展其几何直观能力。

【教学过程】

一、回顾“如何得到圆柱体”

师：在我们的学习过程中，遇到了大量的关于圆柱的“解决问题”。在这些问题中，圆柱体是怎么得到的？出现过哪些形式？（课件呈现）

●卷出来——长方形纸卷出侧面。

●切割——从长方体中切割而得。

●旋转——纸片旋转运动，纸片为圆柱的半个截面。

●平移——水柱管道运动，水柱运行的长度作为圆柱的高。

师：我们已经画过了“卷出来”，今天重点研究“切割”“旋转”“平移”。

二、分层研究

1.切割。

师：一个长方体的三种棱长度分别为10厘米、8厘米、5厘米，以不同的面为底面，切出三种尽可能大的圆柱，比较一下它们的体积。

（1）理解信息，想象“切割”的画面。

（2）画简单的草图，找到基本数据。

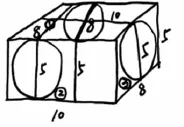
问1：刚才同学们都画了三个草图，有了自己动手画的体验后，你能看懂这个草图吗？（如上图）这样画有什么好处？

生：简单，也能得到基本信息。

问2：那你能从中得到哪些基本信息？

生：①号，底面在上面，直径为8，高为5；②号，底面在前面，直径为5，高为8；③号，底面在侧面，直径为5，高为10。

问3：根据已知的基本信息，你能比较这三个圆柱体的大小吗？

一种确定：③号一定比②号大。

两种猜想：①号比③号大，或者③号比①号大。

用数据验证：①号是4×4×π×5=80π；③号是 2.5×2.5×π×10=62.5π。

问4：你有什么发现？

小结：体积要大，就要尽可能让底面半径大。

【设计意图：学生往往会根据信息去画三个切割图，这对解题而言，支架过于累赘。因此，教师在学生体验后，直接示范简单作图法，再次体验到画草图的目标是找到问题解决的关键信息。草图无需精确到位，合理、简洁即可，甚至可以取巧，只要能帮助找到关键信息就可以。】

（3）变化。

师：从长方体、正方体中可以切割出圆柱体，圆柱体自身也可以再切割，得到小圆柱体。

①把一根长为400厘米的圆柱形木料沿横截面锯成四段，表面积比原来增加了90平方厘米，原来这根木料的体积是多少立方厘米？

②把一根长为400厘米的圆柱形木料沿横截面锯了四次，表面积比原来增加了90平方厘米，原来这根木料的体积是多少立方厘米？

问1：你能画草图、标数据，并列出式子吗？

问2：两道题的草图对比，说说你的理解。

【设计意图：切割是从表面积增加的角度来求出原体积，是学生较为常见的问题。通过题组比较的形式，让学生借助草图深度理解题意，掌握解题的关键点。】

（4）深化。

师：把一个高为10厘米的圆柱沿着底面直径切成相等的两半，表面积增加80平方厘米，这个圆柱的体积是多少立方厘米？先想象，再画草图找基本数据。

师：做完以后，同桌交流所画草图并说一说解题过程。

师：谁来介绍一下自己画草图解答的过程？

【设计意图：这种数据隐含的切割问题比较难，学生借助草图就能轻松理解并解决。画草图之前，一定要让学生多想象，再用图形予以表达，更有利于培养学生的空间感。】

2.旋转。

师：有一张长4厘米、宽3厘米的长方形纸片，以其中的一条边为轴旋转可以得到圆柱体，两种圆柱体的体积分别是多少？

（1）理解题意，进行想象。

（2）教师带领作图。

画好两个长方形→哪一条为轴，就把它“绑”在小棒上→旋转，想象，另一条边就是底面半径。

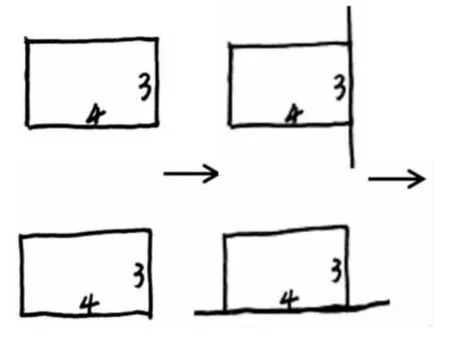
师：这两个圆柱哪个体积大？为什么？

小结：短边为轴、长边为底面半径的圆柱体的体积更大。

【设计意图：学生已经具备利用长方形的两个数据画草图的能力，但是在方法上还不够清晰，需要教师提点、引导、规范来凸显草图的有效性。因此，不再让已经有相关画图体验的学生去通过尝试来积累经验，而是让学生充分想象，然后教师直接示范引领，带着学生有效作图。】

3.平移。

师：在直径0.8米的水管中，水流速度是每秒2米，那么1分钟流过的水有多少立方米？

师：确定形成了圆柱吗？能找到关键信息试着画一画草图吗？

（反馈交流草图，感受草图的作用）

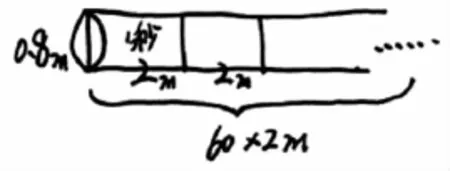
【设计意图：动态的水柱是圆柱体，对学生而言是比较难以理解的，借助草图，学生的理解难度就下降了。1分钟是60秒，也是一个较大的数据，教师可以引导学生采用推想简画的策略，让学生在学习和运用策略的过程中，感受策略对于解决问题的价值，并形成一定的策略意识。】

三、全课总结

师：关于画圆柱的变化图，你有什么收获？

【教学建议】

学生在学习圆柱表面积、体积问题时，最大的困难不是根据公式进行计算，而是其中的“变化”，需要在数与形两个层面深度理解。本课的教学时机为学生学习圆柱的表面积和体积之后，一旦本课的教学目标达成，练习课的课时就可以适当缩短。从某种角度而言，这是一种学科内部的课程整合。在实际教学中要注重以下两点：

一、对“如何得到圆柱体”，要从“问题”中抽取出直观

问学生“圆柱体是怎么得到的，出现过哪些形式？”学生的快速回答离不开教师平时对“问题”特征的归纳。比如当学生遇到“从长方体中切割出圆柱”的时候，要动态演示，给学生留下“切割”的动态印记，帮助学生看到问题的时候，就能想象出大致的运动形式。学生脑海中有这样的“痕迹”，就有助于后续进行抽象作图，解决较为复杂的问题。

二、“平移”难点的突破，要顺着学生的思考过程

水柱的流动，类似“平移”一段距离得到圆柱体。将已知的水流速度、流动时间和管道半径的问题和具体的圆柱体关联起来，学生有一定的困难。突破这一难点，学生要经历的思考过程有三步：一是理解流动的水柱是圆柱，流动的距离也就是路程，路程=速度×时间，教师最好给出形象的照片图辅助理解；二是能指认水柱（圆柱）的底面（横截面）大小和管道半径有关，高度（长）和水流前进的距离有关；三是能结合指认过程画出简单的草图，并标注关键数据。