宽带大规模MIMO-OFDM的联合差分信道估计方案

黄 灿，李素月

(太原科技大学电子信息工程学院，太原 030024)

正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)系统有诸多优势，例如较高的频谱利用率，良好的抗多径干扰的能力和抗窄带衰落的能力等[1]。在无线通讯用户激增的今天，需要提升更多的系统容量，因此把正交频分复用系统与大规模MIMO系统联合作用，从而实现天线分集与空间复用[2]。当前的通信环境下，可利用的无线带宽频率越来越匮乏，将两种系统结合起来，可以极大地提升频谱资源的利用率，同时还可以针对无线信道频率有选择性衰落环境进行有效处理。

大规模MIMO-OFDM系统有着诸多优点，但在现实的无线传播环境里，由于无线信道有着多径效应，且随时间发生变化，尤其是下行链路，用户端需要估计大量的无线信道参数。此外，对于FDD系统的大规模天线的正交导频设计也是极大挑战，因此，获得准确的信道状态信息(Channel State Information, CSI)是大规模MIMO信道估计的关键所在。

频率选择性信道在不同频点上的衰落特性是不一样的，并且呈现一定的稀疏特性[3-5]，在散射体丰富的多径环境下，无线信道的绝大多数能量集中在信道冲击响应(Channel Impulse Response, CIR)的极少分量上。因此CIR能量不是均匀分布在信道的全部抽头上，使得传统的信道估计方法在大规模MIMO-OFDM系统中，估计精度大大降低，并且导致导频开销增大。最小二乘(Least Square, LS)算法未利用无线多径信道所特有的稀疏特性，需要加入大量的导频，且导频数要多于未知信道参数，才可以准确地估计信道，将导致难以接受的导频开销。

相比LS算法，压缩感知(Compressed Sensing, CS)技术可以较好地对付多径稀疏信道，凭借少量的观测信号，就可以将原始信号几乎完全重构出来，并且精度高，速率快[6]。经典的压缩感知正交匹配追踪算法与传统LS算法相比，用较少导频就能得到较好的重构性能，但计算复杂度过高，并不适用[7]。而子空间追踪(SP)算法不仅重建效果比匹配追踪算法好，运算时间也要低于收缩循环迭代法。利用大规模MIMO信道的空时共同稀疏性[8]，在SP算法的基础上，对其进行结构化和联合差分改进。第一，算法在每一次迭代过程中同时对多个向量进行更新，对稀疏性进行结构化改进，提升算法的重构性能。这里借鉴了文献[10]中结构化的改进思想。第二，算法在进行重构过程中，并不是只处理当前时刻接收到的导频信号，而是联合前一帧的导频信号进行差分，以增强稀疏性，进而提升算法重构的精度。

1 大规模MIMO-OFDM系统模型

1.1 系统模型

考虑一个典型的单小区下行多用户大规模MIMO-OFDM无线通信系统，其中，基站端配置Nt根发射天线，小区内单天线移动用户数为NrNt≫Nr，且信道为频率选择性块衰落模型，如图1所示。

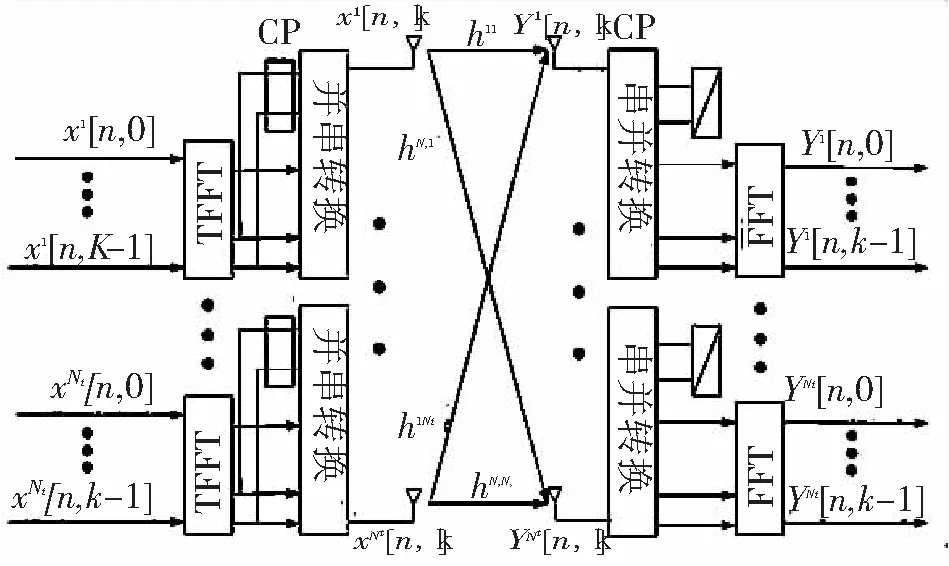
图1 Massive MIMO结构图

Fig.1 Massive MIMO Structure

每个OFDM符号中子载波数设为K.基站第i根天线发射的信号(包含数据和导频)为si∈CK×1i=1,2,...,Nt.信道最大延迟扩展长度为L.那么，用户接收到的导频序列可表达为:

(1)

接收端的信道估计是用接收到的导频信号进行的。具体导频设计方案参考文献[10]设计的非正交导频方案。那么，从接收到的信号y中提取出接收到的导频信号yΩ，可表示为:

(2)

集合Ω表示子载波集合1,2,3,...,K中随机选取导频所在的位置。Ci=diagci，ci∈Cp×1表示第i根天线发送的导频信号，上标p表示每个OFDM符号中的导频数，根据集合Ω取FL的子矩阵得到FLΩ.将公式(2)简化，可得：

yΩ=Ψh+nΩ

(3)

其中Ψ=[C1FLΩ,C2FLΩ,...,CNtFLΩ]

1.2 大规模MIMO信道的时间和空间共同稀疏性

CIR集合hi=hi1,hi2,...,hiLT中，非零元素抽头数量远小于零元素抽头数量，呈现时间上的共同稀疏性。

(4)

大规模MIMO信道的空间共同稀疏性指的是所有发射天线所对应的子信道的多径位置相同。

令hΣ=h1,h2,...,hLT，其中he=h1e,h2e,...hNte，e=1,2,...,L.由空间共同稀疏性可以得知，零元素所在位置的值仍然为零，那么就是说所对应的hκ(其中κ∈1,2,...,L)所有元素为零；同理，非零元素所在位置的值仍然为零, 那么就是说所对应的hζ(其中ζ∈1,2,...,L)所有元素仍非零。因此，结构化的矩阵hΣ有更强的稀疏性。

1.3 大规模MIMO信道的时间相关性及联合差分方案

考虑到实际信道是频率选择性块衰落的，也就是说，若基站与移动台之间几乎没有相对移动，可认为一定时间内信道基本保持不变，或相邻两帧OFDM符号所经过的信道状态只有微小的变化[11-12]。

利用大规模MIMO信道的这种时间相关性的特性，提出联合差分方案，以增强稀疏性，进而提升算法重构的精确度。

传统的方法是将接收到的每一帧导频序列符号直接用算法对其进行信道估计。而联合差分并不是只处理当前时刻接收到的导频序列符号，而是联合前一帧导频信号进行差分，得到差分下的信道冲击响应(Differential CIR, D-CIR)，这就是信道估计的联合差分方案。可以表示为:

Δht+1=ht+1-ht

(5)

从图2可以看出，利用时间相关性的差分结构的CIR有更好的稀疏性。

图2 差分CIR结构示意图

Fig.2 The diagram of differential CIR

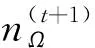
(6)

由公式(6)可知，联合差分后的Δh(t+1)具有比原始h(t+1)更加良好的稀疏性，这意味着在一定导频开销的情况下，可以使得CS算法有更好的恢复性能。也就是说，减少导频开销可以获得相同的性能[13]。

在得到D-CIR之后，可以通过与上一帧的CIR相加来获得当前的信道冲击响应。

2 提出的联合差分结构化SP算法

2.1 传统SP算法

匹配追踪算法是最初的贪婪算法，此后又有很多对其改进的方案，例如正交化匹配追踪(OMP)算法等[14]。再引入回溯思想后，贪婪算法发展到SP算法，其本质是从原子库中选择多个关联较大的原子，于此同时，删去部分原子，从而提高算法效率[15-16]。每次迭代过程中，支撑集包含K个原子。SP算法不仅重建效果比匹配追踪算法好，运算时间也要低于收缩循环迭代法。

压缩感知理论应用于MIMO的信道估计，期初是OMP算法[17]，而后又发展到SP算法[18]，无论是OMP算法还是SP算法，都是压缩感知理论中的具体算法。在文献[17]中，MIMO的信道估计应用了压缩感知理论中的OMP算法。在文献[18]中， MIMO信道估计中应用SP算法的理论研究，并详述了应用SP算法的好处和理由。但这两篇论文都没有根据MIMO信道特点和SP算法的不足进行改进，仅仅只做了简单的应用而已。

SP算法的重要特点在于寻找生成正确子空间的K个列向量的方法。该算法包含测量矩阵中的K个列向量的列表，对子空间的最初估计的是测量矩阵中与实际信号y的K个最大相关的列。为了修正对子空间的最初估计，SP算法会检测包含K个列向量的子集，检测这个子空间是否可以很好地重建信号。重建信号与实际信号之间残差没有达到算法的要求，则需要更新这个列表。该算法会通过保留可靠的，丢弃不可靠的候选值，同时也加入相同数量的新候选值来更新子空间。更新的原则是新的子空间重建信号残差要小于更新前的子空间重建信号残差，该算法在一定条件下能够确保重建，并且SP可以确保下一个迭代循环能够找到更好的子空间。

SP算法具体如下[14]：

输入：测量值y，感知矩阵φ，稀疏度K.

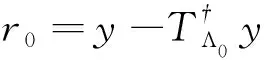
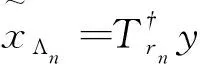
2.2 提出的联合差分结构化SP算法

SP算法的不足之处在于在迭代过程中，每一次迭代只更新一个稀疏向量，没有充分利用大规模MIMO信道的空间共同稀疏性[15]，不但会在迭代阶段消耗大量时间和能量，而且会使算法精度下降。

从增强未知矩阵的稀疏性可以提高压缩感知重构的精确度的方面出发，并且结合稀疏信道空时相关稀疏性的特点，从结构化和联合差分两个方面提升其稀疏性，提出的联合差分结构化SP (JDSSP) 算法。

JDSSP算法具体如下：

输入：测量值y(t)、y(t-1)，上一时刻CIR矩阵h(t-1)，感知矩阵φ，稀疏度K.

(1)初始化：y=y(t)-y(t-1)；余量V1=y；循环次数k=1；索引值集合Ω=φ

(2)Z=φHVk；

(4)Ω=Ω∪suppc〉K合并集合;

(5)Γ1=Ω∪[Ω+L]∪,...,∪[Ω+L(M-1J)]合并集合；

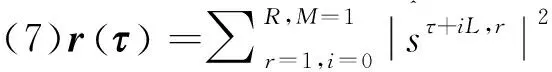
(8)Ω=suppr〉K;

(9)Γ2=Ω∪Ω+L∪,...,

∪Ω+LM-1

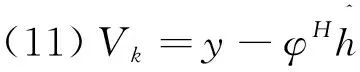
(12)若满足‖Vk‖F>‖Vk-1‖F则停止迭代；否则令k=k+1,转步骤(2).

JDSSP算法的实现思路是用户端接收到当前的导频信号之后，联合前一帧导频符号求差分，得到差分信号，完成联合差分，提高其稀疏性。差分信号在每一次迭代过程中都对多个稀疏向量进行更新而非原算法每次迭代只更新一个向量。将每一个CIR向量中同一个位置的抽头都视为一个整体。文献[5]在基站侧对反馈信号有类似的处理。

步骤(1)(2)体现了联合差分的思想，步骤(3)-(9)表示了稀疏性的结构化。在此说明：若对2.1节中SP算法考虑联合差分改进，而不考虑稀疏性的结构化改进，则此算法称为联合差分SP(JDSP)算法。若对2.1节中SP算法只考虑稀疏性的结构化改进，而不考虑联合差分改进，则称此算法为结构化SP(SSP)算法。在文献[10]中，对压缩匹配追踪(CoSaMP)算法有类似稀疏性结构化的改进。

3 仿真数据及结果分析

本节利用MATLAB仿真软件对所提出的大规模MIMO-OFDM无线通信系统中的JDSSP算法进行性能验证。系统参数设为基站侧发射天线数量为64根，系统中系统子载波数为1 024，信道多径数为64，且每个信道为独立同分布的瑞利衰落信道，噪声由零均值单位方差的复高斯随机变量组成。系统模型为国际电信联盟车载B(ITU-B)信道模型。仿真中，还对所提出的JDSSP算法与JDSP算法、SSP算法、SP算法进行了比较。在性能的衡量方面，用归一化均方误差(NMSE)来作为指标。NMSE越小，估计出来的结果误差就越小，则表明估计性能就越好。

(7)

图3比较了在不同信噪比需求下各种算法的NMSE.在仿真中为了更好地进行各种算法性能的比较，不仅考虑了信噪比(SNR)取值从0 dB至30 dB的情况，还选取导频占比ζ=0.60 (即导频数占子载波数的60%).图3给出了不同信噪比情况下各算法的估计性能。从图中可以看出JDSSP算法的估计性能优于其它算法，接下来估计性能依次是JDSP算法、SSP算法，估计性能最差的是SP算法。

图3 提出的JDSSP算法, JDSP算法, SSP算法, SP算法性能比较图(导频占比0.60)

Fig.3 NMSE performances of JDSSP, JDSP , SSP, SP algorithm (pilot ratio 0.60)

图4和图3基本一致，不同的是导频占比ζ=0.35 (即导频数占子载波数的35%).图4给出了不同信噪比情况下各算法的估计性能。

导频指的是在OFDM系统中，通过在特定的子载波上插入一些已知的数据。在接收端根据这些已知的数据进行时间和频率上的信道测量与估计.提高估计的精度可以提升接收端对信号的解调性能。

然而，导频数据占用了一定的传输资源。为了提高系统的频谱效率，必然要降低导频数据在每一帧OFDM符号中的比例，即降低导频占比。降低导频数量势必会降低估计性能。如在图4中，当导频数减少时，各种算法的估计性能都有所降低。并且，JDSP算法、SSP算法和SP算法已经不能随着SNR增大而进行准确的信道估计。而JDSSP算法的估计性能虽然因为导频数量减少而有所降低，但仍优于其它算法，并且，估计性能仍然比较良好。

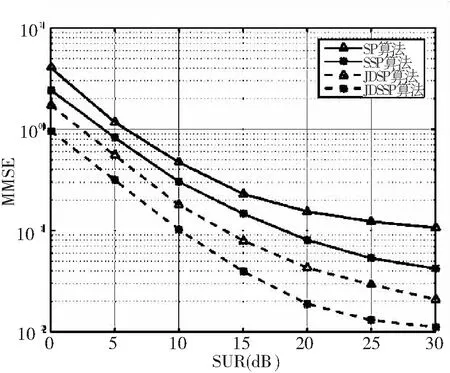
图4 提出的JDSSP算法, JDSP算法, SSP算法, SP算法性能比较图(导频占比0.35)

Fig.4 NMSE performances of JDSSP, JDSP , SSP,SP algorithm (pilot ratio 0.35)

综合图3和图4的仿真数据，结果表明SP算法和SSP算法的导频占比为0.60时的估计性能，与利用联合差分方案下的SP算法和SSP算法(即JDSP算法和JDSSP算法)的导频占比为0.35时的估计性能大致相同。说明了联合差分方案增强了稀疏性，同等估计性能条件下，降低了导频开销，节省了频谱资源。

4 结束语

根据大规模MIMO信道的空时共同稀疏性的特点，从联合差分和结构化两方面对SP算法进行改进，提出JDSSP算法。不仅优化了估计性能，同时还降低导频开销，节省能源消耗和频谱资源。符合我国对于绿色通信成为发展趋势的要求[16]。

压缩感知算法作为信道估计的重构算法需要提前知道稀疏度作为先验信息。而在实际无线通信环境下，稀疏度是很难被准确获取的，接下来的工作主要针对压缩感知应用于信道估计的这点不足进行自适应化改进，使重构算法无需获取稀疏度作为先验信息。