混合臂式高空作业车变幅系统动态建模与分析

孙 迪，高崇仁，朱建学，殷玉枫

(1.太原科技大学 机械工程系，太原030024；2.河南江河特种车辆有限公司，河南 新乡453400)

高空作业车是指运送工作人员和使用器材到现场并进行空中作业的专用车辆。由于混合臂式高空作业车在臂架变幅过程中相对运动较为复杂，目前针对高空作业车运用基础力学理论解析推导动力学微分方程的研究主要集中在直臂式和折臂式的车型上，即便是混合臂式车型也多运用大型仿真模拟软件建模和仿真，少有解析推导的佐证来增强说服力[1-4]。现阶段的动力学分析中对高空作业车臂架刚柔耦合振动分析、工作平台调平分析及臂架轨迹规划等方面的研究较为全面[5-9]，不过缺少臂架变幅运动对伸缩、变幅液压缸流量、油压影响的进一步分析。本文基于拉格朗日方程对上臂系统和下臂系统均具有一节伸缩臂的一般混合臂式高空作业车进行建模并推导运动微分方程，而后推导臂架在变幅过程中油缸受力、油压、流量等相关参数随时间变化的关系。假定一种臂架转动与伸缩同步进行时的变幅运动，基于最小二乘原理运用MATLAB编程进行数值求解并分析结果、验证结果。

1 臂架系统模型的建立

混合臂式高空作业车的实际物理系统比直臂式和折臂式都要复杂，现将臂架系统模型作如下简化处理：

只考虑变幅运动而不考虑回转运动，以减少与油缸参数关系不大的臂架自由度；将臂架模型作为刚体进行推导；假定臂架质量分布均匀，油缸质量纳入臂架质量，作业平台质量集中于质心；不考虑铰点及臂架间摩擦；将飞臂与作业平台视为一体，简化如图1，B3B3'视为调平油缸。

1.1 广义自由度的确定

由于只考虑变幅平面的运动，所以以下臂系统起始端点O为坐标系原点，建立变幅平面直角坐标系xoy.以下臂系统与水平轴x的夹角θ1，下臂系统第二节臂伸出长度l1，下臂系统与上臂系统之间的夹角θ2，上臂系统第二节臂伸出长度l2以及作业平台内侧边缘与上臂系统的夹角θ3作为臂架系统的广义自由度。因θ3=90°-θ2+θ1，所以臂架系统相互独立的自由度为θ1、θ2、l1、l2，即所建立系统拉格朗日方程的广义坐标为q=[θ1θ2l1l2].

图1 混合臂式高空作业车臂架系统机构简图

Fig.1 Schematic diagram of boom system of hybrid arm type aerial working vehicle

1.2 广义力的表示

根据分析力学中对广义力的表述[10]，设作用在第i个质点上的主动力的合力Fi在三个坐标轴上的投影分别为(Fix，Fiy，Fiz)，则广义力

(k=1，2，…，n)

得到除保守力以外的其它力的广义力为

Q1=Fb1m1sin(θ1+Φ1)-Fb2(2l1+2l10+2L12+a)sin(β+Φ2+2θ1)-Fb2(b+m2)sin(β+Φ2+θ2)+2(l1+l10+L12+a)Fs2sinθ2+2(l1+l10+L12+a)Fb3sin(θ2-Φ3)+(2b+2l20+2l2+2L22-n3)Fb3sinΦ3

Q2=Fb2(b+m2)sin(β+Φ2+θ2)-Fb3(2b+2l20+2l2+2L22-n3)sinΦ3

Q3=Fs1+2Fb2cos(β+Φ2)-2Fs2cosθ2-2Fb3cos(θ2-Φ3)

Q4=Fs2+2Fb3cosΦ3

(1)

式中：Q1、Q2、Q3、Q4分别为与广义坐标对应的广义力；Fb1、Fb2、Fb3、Fs1、Fs2分别为各油缸对臂架的作用力；其余尺寸参数符号如图1.

1.3 系统动能的表示

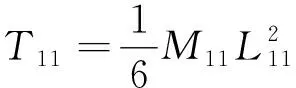
式中：T11、T12、T21、T22、T3分别为下臂系统一节臂、二节臂，上臂系统一节臂、二节臂，作业平台动能；M11、M12、M21、M22、M3分别为分别为下臂系统一节臂、二节臂，上臂系统一节臂、二节臂，作业平台质；x21、y21、x22、y22、xp、yp分别为上臂系统一节臂、二节臂，作业平台质心坐标；其余符号同式(1).

1.4 系统势能的表示

由于将臂架系统视为刚体且不考虑铰接点与臂架间摩擦，所以系统总势能即为系统重力势能。设系统势能零点为x轴。由于下臂系统和上臂系统连接处B2'S2'相对整个臂架系统尺寸较小，为了便于计算忽略此段尺寸，则系统总势能为

(2)

式中：V为系统总势能；其符号同式(1).

1.5 变幅系统动力学方程的建立

非保守系统的拉格朗日方程为:

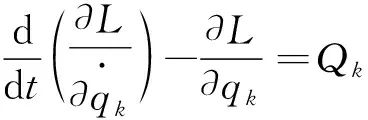
(3)

其中：动势L=T-V ；Qk为除保守力以外的其他施加力的广义力。

将系统广义力、动能和势能代入式(3)，则系统动力学方程如下：

(4)

(5)

(6)

(7)

式中：各符号同式(1).

2 驱动油缸相关参数的推导

高空作业车变幅系统的执行机构是下臂系统变幅油缸b1、伸缩油缸s1、上臂系统变幅油缸b2、伸缩油缸s2及调平油缸b3，油缸简图如图2.

图2 驱动油缸简图

Fig.2 Drive cylinder diagram

2.1 油缸流量q

假设任一时刻油缸b1、b2、b3的长度为ri，由三角几何关系有

(8)

式中：m、n为变幅三铰点两边长度；θi为各节臂间夹角，见图1.

假设任一时刻油缸b1、b2、b3速度为vi，无杆腔内直径Di，有杆腔杆径di，则流量

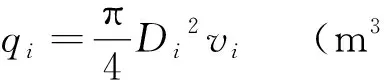
(9)

联立(8)(9)式得到油缸流量为

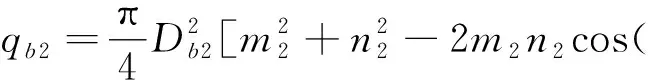
式中：qb1、qb2、qb3分别为各变幅油缸流量；Db1、Db2、Db3分别为各变幅油缸无杆腔直径；其余符号同(1)式。

2.2 油缸油压p

对各驱动油缸任意时刻由牛顿第二定律有∑F合=ma，且∑F合=F+p1A1+p2A2.考虑到油缸质量相对整个臂架系统质量较小，臂架变幅速度一般较小，以致加速度较小，有∑F合=F+p1A1+p2A2=0.当有杆腔伸出时，有

(10)

式中：Fi为油缸b1、b2、b3、s1、s2与臂架连接点受力；Di为油缸b1、b2、b3、s1、s2无杆腔内直径；di为油缸b1、b2、b3、s1、s2有杆腔内杆直径；m为油缸及液压油质量；A1、A2为无杆腔、有杆腔面积；p1、p2为无杆腔、有杆腔压力。

3 数值仿真

3.1 基本参数

选取某26 m高空作业车，模拟的工况：下臂系统以0.01 rad/s的角速度变幅至下臂系统最大角度75°，上臂系统始终保持水平，下臂系统伸缩臂以0.1 m/s的速度同步匀速伸出至最大行程5 m后停止伸出，上臂系统伸缩臂以0.1 m/s的速度同步匀速伸出至最大行程6.4 m后停止伸出，整个过程130 s，期间作业平台一直保持水平。

3.2 求解方法

已知运动条件

表1 高空作业车相关参数

Tab.1 Related parameters of aerial vehicle

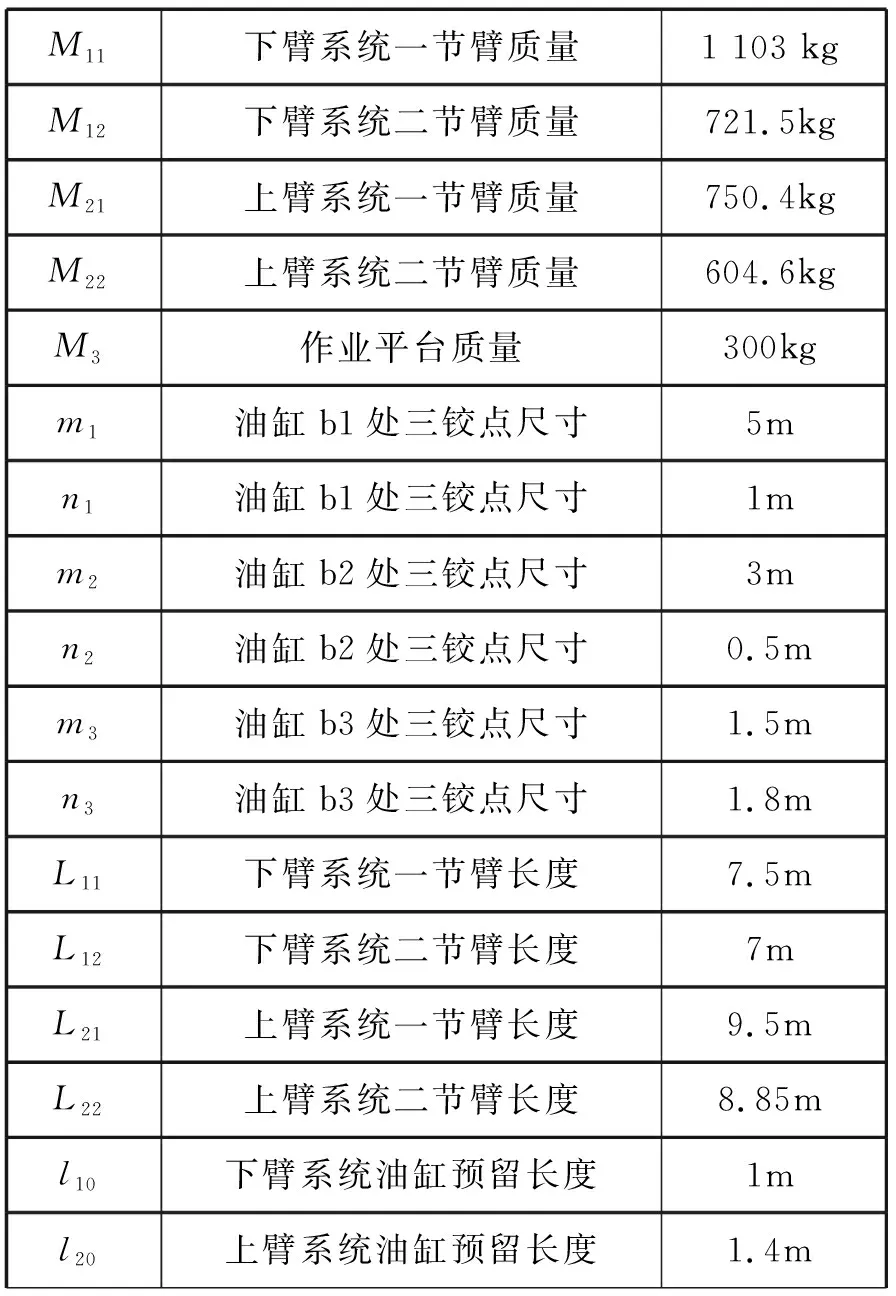
M11下臂系统一节臂质量1 103 kgM12下臂系统二节臂质量721.5kgM21上臂系统一节臂质量750.4kgM22上臂系统二节臂质量604.6kgM3作业平台质量300kgm1油缸b1处三铰点尺寸5mn1油缸b1处三铰点尺寸1mm2油缸b2处三铰点尺寸3mn2油缸b2处三铰点尺寸0.5mm3油缸b3处三铰点尺寸1.5mn3油缸b3处三铰点尺寸1.8mL11下臂系统一节臂长度7.5mL12下臂系统二节臂长度7mL21上臂系统一节臂长度9.5mL22上臂系统二节臂长度8.85ml10下臂系统油缸预留长度1ml20上臂系统油缸预留长度1.4m

对作业平台有

(11)

3.3 结果与分析

由图3、图4看出变幅油缸b1受力初始值为30.83 kN，在5 s时达到正向最大值39.01 kN，22 s减小到0后负向增大，在80 s后基本稳定在30 kN；变幅油缸b2受力初始值为30.83 kN，55 s增加到最大值37.79 kN，随后缓慢减小到15.2 kN；伸缩油缸b2受力初始值为15.54 kN，在55 s增加到最大值24.26 kN；随后缓慢减小到14.06 kN；简化的调平油缸b3受力初始值为负向31.77 N，随后减小到0，55 s后负向增大到544.7 N；伸缩油缸s2初始值为43.16 N，随后变化趋势与b3受力相反，130 s增大到715.8 N.

图3 油缸b1、b2、s1受力变化曲线

Fig.3 Force change curve of cylinder b1, b2, s1

图4 油缸b3、s2受力变化曲线

Fig.4 Force change curve of cylinder b3, s2

变幅油缸b1、b2，伸缩油缸s1在变幅过程中受力大小在同一个数量级，达到10的5次方N；简化的调平油缸b3，伸缩油缸s2在变幅过程中受力大小在同一个数量级，达到10的2次方N.说明此工况下各油缸受力相差还是比较大的，达到1 000倍。在此模拟运动下，上臂系统保持水平，则θ3保持90°不变，Fb3与Fs2在水平方向上变化趋势相反。

在得到油缸受力的基础上，结合式(10)，当保持油缸一侧(进油口)压力值时得到油缸另一侧(出油口)压力随时间变化的图像。由图5、6、7、8、9、看出，在变幅仿真过程中，当b1无杆腔(进油口)油压最大为0.5 MPa且整个过程一直保持此油压时，有杆腔油压最大值接近系统最大压力20.7 MPa，但最小值小于0，因此整个过程无法保持进油口油压恒定不变且整个过程出油口油压变化也较大；当b2无杆腔(进油腔)油压最大为13 MPa且整个过程一直保持此油压时，有杆腔油压最小1.7 MPa，最大接近系统最大压力20.7 MPa，整个过程出油口油压变化较大；当b3无杆腔(进油腔)油压最大为10 MPa且整个过程一直保持此油压时，有杆腔油压最大值接近系统最大压力20.7 MPa且整个过程变化较平稳；当s1无杆腔(进油腔)油压达到13.5 MPa时，有杆腔油压在10 s到90 s期间最小值将小于0，但又要保证有杆腔油压小于系统最大压20.7 MPa，所以将10 s到90 s期间无杆腔油压至少调整至18.8 MPa才能保证有杆腔油压大于0(如图8)，整个过程进油口不能保持恒压，且进、出油口油压变化均较大；当s2无杆腔(进油腔)油压最大为12.1 MPa且整个过程一直保持此油压时，有杆腔最大值接近系统最大压力20.7 MPa且整个过程变化平稳。

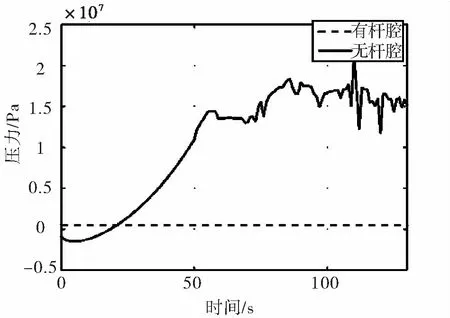
图5 油缸b1压力变化曲线

Fig.5 Oil pressure curve of cylinder b1

各油缸流量如图10、11.伸缩油缸s1、s2匀速伸出，其流量也保持不变；θ1、θ2匀速变化时，变幅油缸b1、b2作变速运动，其流量变化不大且在10的-4次方m3/s数量级。由于模拟运动使θ3一直保持90°，则调平油缸b3流量恒为0.

图6 油缸b2压力变化曲线

Fig.6 Oil pressure curve of cylinder b2

图7 油缸b3压力变化曲线

Fig.7 Oil pressure curve of cylinder b3

图8 油缸s1压力变化曲线

Fig.8 Oil pressure curve of cylinder s1

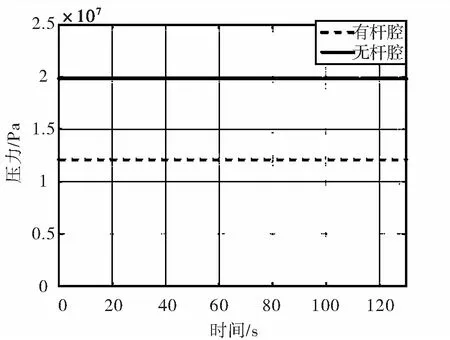
图9 油缸s2压力变化曲线

Fig.9 Oil pressure curve of cylinder s2

图10 油缸b1、b2、b3流量变化曲线

Fig.10 Flow curve of cylinder b1

图11 油缸s1、s2流量变化曲线

Fig.11 Flow curve of cylinder s1,s2

式中：各符号同式(1).

得到作业平台在x、y方向上速度的模拟值vxm、vym与理想值vxl、vyl，如图12.

本文所述方法经数值求解得到的作业平台x、y方向上的速度与由运动学正解得到的理想值吻合度较好，从而也验证了此方法的正确性。小部分误差的原因在于在求系统势能时为简化计算，忽略了尺寸较小的n2段，系统动势L比实际值偏小；Matlab进行数值求解时运用的fsolve函数对搜索初始值的要求较高，求解时得到的数值解会随初始值的不同有所波动，从而对系统造成一定误差。

4 结论

本文运用分析力学理论对混合臂式高空作业车变幅系统建立了运动微分方程，利用该方程进行数值模拟得到变幅过程中油缸受力、油压、流量的时间历程曲线。分析得出：

图12 作业平台x、y方向速度变化曲线

Fig.12 speed change curve of operating platform along x and y direction

(1)在给定臂架运动条件下，运用本文所述方法得到变幅过程中变幅油缸b1、b2，伸缩油缸s1所受作用力相比调平油缸b3，伸缩油缸s2所受作用力较大，油缸设计时须优先对b1、b2、s1进行强度分析。

(2)在给定臂架运动和各油缸一侧(进油口)压力值的条件下，油缸b1、b2、s1另一侧(出油口)的油压变化较大，油缸设计时须对b1、b2、s1进行动强度分析，以进一步研究结构在动载荷作用下的应力与变形等响应；油缸b3、s2另一侧(出油口)的油压变化较平稳，可主要进行静强度分析；

(3)在给定臂架运动条件下，各油缸流量变化较平稳，可考虑使用定量泵节流调速系统；

(4)由作业平台理想速度与数值解得到的速度对比，证明了本方法的正确性。