热循环载荷下POP堆叠电子封装的可靠性研究

2018-11-22 10:48刘昭云杨雪霞

太原科技大学学报 2018年6期

刘昭云，杨雪霞

(太原科技大学应用科学学院，太原030024)

POP堆叠由于可以将多个封装叠放在一起的结构，使得整个封装更加高效和小巧。其本身可以在装配前对各个组件部分分别进行性能测试，提高了整体封装的良品率，降低了总成本[1],正在越来越多的运用到各个电子产品中。但其复杂的空间结构，使得散热成为了一个难题，热寿命成为制约POP堆叠封装可靠性的一个重要因素。[2]对在热循环下的POP堆叠进行热寿命的分析是十分有意义的。

对于POP堆叠封装的力学性能研究，前辈唐修胜在《温度冲击载荷下POP堆叠封装可靠性研究》[3]中，用有限元方法分析POP堆叠封装的可靠性，利用Kencht-Fox焊点寿命预测模型进行计算。王洋在《不同温度环境下POP堆叠封装的可靠性研究》[4]中，对比了不同温度环境下相同尺寸POP以及不同尺寸POP相同温度环境下的可靠性。陈冬琼在《堆叠封装(POP)的可靠性研究》[5]中，根据Styed累积等效蠕变应变模型预测焊球的疲劳寿命。

以上对于POP堆叠的可靠性的研究，分别考虑了在不同的粘塑性模型下的焊球材料属性，但没有考虑Anand粘塑性模型在温度循环载荷下的情况[6]。本文在前人工作的基础上考虑Anand粘塑性模型的情况[7]，构建双层堆叠双阵列焊球排布模型来研究和分析焊球在温度循环时的力学行为，塑性应变的危险点等，从而讨论POP堆叠在温度循环下的可靠性。

1 ANSYS中POP堆叠封装热循环分析

1.1 建立封装有限元模型

POP(package on package)堆叠的最显著的特点就是把具有多引脚的逻辑元件和高集成度的存储元件通过焊点的连接，叠加安装在垂直的方向上。[8]本文所讨论的POP模型来源于Amkor公司所研发生产的POP堆叠芯片，顶层放置安装的是PScfBGA封装的逻辑元件，在底层的安装的是以SCSP形式封装的存储元件。[9]

在本文的讨论中,将封装中的焊点处几何模型假设为了理想的球形[10]；假设POP封装之中的芯片、基板与塑封层等处的材料均为各向同性的线弹性材料，且各种材料都均匀分布的。[11]

几何参数如表1所示[12]，按照下表中的尺寸制作完成的模型图如图1与图2所示。图1为总体的俯视图，图2为核心部分(即总体俯视图中的左上角芯片所在位置)的放大视图。

图1 三维模型图

Fig.1 3Dmodeldiagram

图2 三维模型图

Fig.2 3Dmodeldiagram

表1 POP堆叠封装模型各部分尺寸

Tab.1 POP stacked package model dimensions

顶层封装(mm)底层封装(mm)芯片6×6×0.16×6×0.1焊盘高度0.020.02焊球直径0.80.8焊球高度0.60.6焊球间距1.21.2焊球边距0.60.6基板20×20×0.1320×20×0.13塑封20×20×0.4612×12×0.46PCB板200×140×1.5

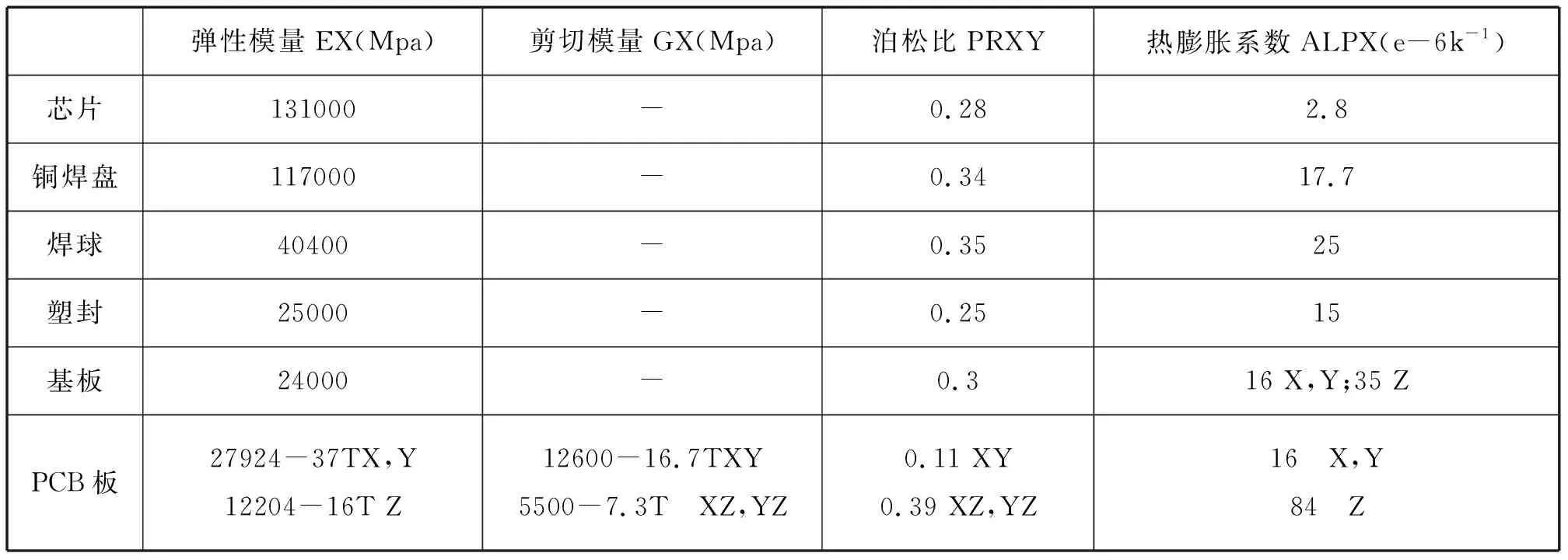
表2 POP堆叠封装各部分材料参数

Tab.2 POP stack package material parameters

弹性模量EX(Mpa)剪切模量GX(Mpa)泊松比PRXY热膨胀系数ALPX(e-6k-1)芯片131000-0.282.8铜焊盘117000-0.3417.7焊球40400-0.3525塑封25000-0.2515基板24000-0.316 X,Y;35 ZPCB板27924-37TX,Y12204-16T Z12600-16.7TXY5500-7.3T XZ,YZ0.11 XY0.39 XZ,YZ16 X,Y84 Z

表3 修正过的Anand模型参数

Tab.3 Modified Anand model parameters

焊点材料S0/MpaQ/R(K)A(s-1)ξmh0 /MPa^S/MPanαSn3Ag0.5Cu45.974605.87e620.0942935058.30.0151.5

在应用ANSYS有限元软件进行建模模拟的过程中，在建模符合实际工件的几何尺寸的基础上，还要进一步的考虑在材料的力学特性上更接近真实情况。[13]我们选用与真实情况贴近的属性参数，保持与实际表现出的情况一致。本文中所讨论的POP堆叠封装的各个部分材料参数如上表所示[14]。

边界条件考虑外围模型为固定约束，对称界面为对称约束，同时注意细化核心部分的网格划分，使得模拟的结果接近真实值，在外部区域则进行粗划分，减小不必要的计算量，有限元网格模型图如下图3所示,核心部分放大图如图4所示。

施加的温度循环载荷符合美国的ML-STD-883标准，温度曲线如图3所示。

图3 有限元网格模型

Fig.3 Mesh model

图4 有限元网格模型

Fig.4 Mesh model

图5 温度曲线图

Fig.5 Temperature curve

1.2 仿真结果云图与曲线图分析

从以下的位移云图中，我们可以到的是周围边界固定时，由于温度上升，芯片受热膨胀，且周围的材料热膨胀系数不配合，从而出现的情况，在这种情况下中心区域的部分位移最大，而外延区域较小。

从焊点塑性应变云图中，我们能够看出，最大塑性应变的发生点是，位于对角线位置的焊点，而且是底层的，与PCB板直接相连的焊点，这与我们之前的理论是相符合的，同时，关键焊点的位置也是符合实际情况的。

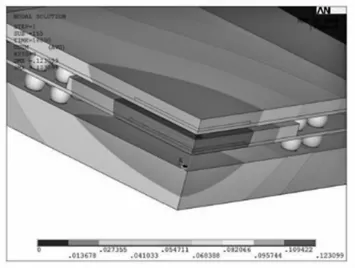
图6 POP堆叠封装位移云图

Fig.6 Displacement nephogram of POP stack

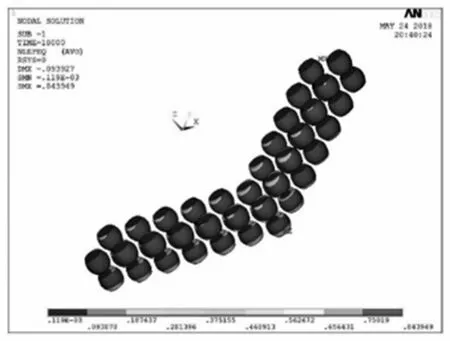
图 7 焊点处的等效塑性应变云图

Fig.7 Equivalent plastic strain nephogram of solder joints

从以下的图中，我们可以看出芯片在温度循环中的受力情况，首先，整个芯片部分的应力，大体上是相对均匀，这是由于外侧在受到温度载荷时，变形膨胀收到了周围的塑封的限制，产生了较大的应力。

(a)底层 b)顶层

图8 芯片的Von Mises应力分布

Fig.8 Von Mises stress distribution on the chip

从下面的两个图中，我们可以看到顶层和底层焊点的最大应力都分别出现在顶层与底层焊点的外围排布，而且在顶层的焊点处最大应力位置出现在上表面，底层焊点的最大应力点出现位置在下表面，这种情况正是因为焊点与基板、PCB材料的热膨胀系数不匹配，在升降温度的过程中形变不配合，导致出现了应力集中情况。同时，我们从数据中可以看出，顶层焊点的最大应力值为34 MPa，底层焊点的最大应力值为42 MPa，从这一数值可以看出，顶层焊点所受到的应力是要小于底层焊点的。

(a)底层

(b)顶层

图9 焊点处Von Mises应力云图

Fig.9 Von Mises stress nephogram of solder joints

为了更加清晰的看出顶层与底层焊料球中应力的分布，现在将外围的焊料球沿Y轴方向编号，其中外围焊料球的定义，编号结果如下图所示，同时，分布将右侧外围焊料球应力变化趋势图列出见曲线图，显示出了在顶层焊点、底层焊点处最大应力的分布，底层焊点的最大应力点在最外围的对角处，而顶层处焊点的最大应力点则在中心向对角方向的第五个焊点处。

图10 焊点编号

Fig.10 Number of solder joints

图11 焊点处最大应力分布

Fig.11 Maximum stress distribution at th solder joints

从下面的图可以看出在关键焊点(等效塑性应变最大的点)处的等效塑性应变分布状态，可以看到：等效塑性应变最大的点出现在与PCB板相接处的平面上;2.等效塑性应变最大的点的位置正好处于关键焊点分布位置的外围，即整个焊料球阵列的最外围。

图12 关键焊点处的等效塑性应变分布

Fig.12 Equivalent plastic strain distribution at key solder joints

下图中可以看到，关键焊点处的等效塑性应变随时间的变化曲线，Von Mises应力分布随时间的变化曲线，Von Mises塑性应变随时间的变化曲线。通过这三张图的比较，我们发现这三者都与温度的变化同步发生，且应力的变化与温度相反，应变的变化与温度相同，并且可以发现，塑性应变有随着循环次数累积的特性，从Von Mises塑性应变的图中，我们可以读取出塑性应变的幅度差值，得到本文所预测的POP模型的寿命。

图13 关键焊点处等效塑性应变随时间变化

Fig.13 The change of the equivalent plastic strain at the key solder joint with time

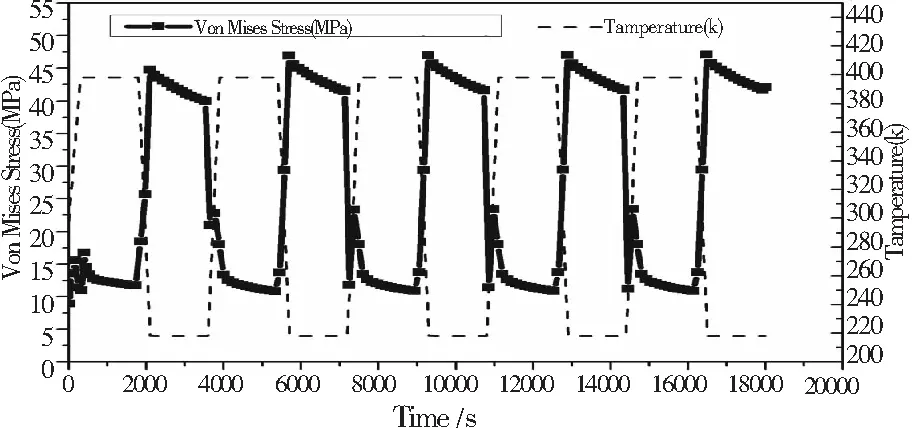
图14 关键焊点处Von Mises应力随时间变化图

Fig.14 Time change diagram of Von Mises stress at key solder joint

图15 关键焊点处Von Mises 塑性应变随时间变化图

Fig.15 Time dependent change of plastic strain of Von Mises at key solder joints

1.3 POP堆叠封装寿命计算

使用修正的Manson-coffin模型来估算焊点处的疲劳寿命。

(1)

上式中的疲劳延性系数C可以通过以下的方程得到：

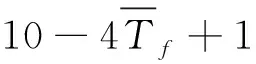
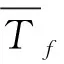
通过图线可以得到Δεp为0.007999；将各个参数带入到公式得到估计的寿命值为6406(cycle).

2 结论