基于双种群的Pareto局部搜索算法
汪 欣,夏 超
(南京航空航天大学 计算机科学与技术学院,江苏 南京 211100)
0 引 言
实际中大部分的优化问题都是组合优化问题,在很多情况下各个目标之间都是相互冲突的,即对于一个目标上的改善很有可能会导致其余一个或几个目标性能的降低。因此多目标优化的目的是对多个目标上进行权衡,使得优化结果能够在各个目标上都尽可能达到最优。进化算法是一种基于种群的多点搜索方法,已经在很多多目标优化问题[1]中得到了应用[2]。当前已经有很多算法在2~3个目标的组合多目标优化问题中取得了良好的效果,但是在超多目标(3个以上目标)上的表现不佳。针对超多目标的问题的特性,提出了一种基于双种群的Pareto局部搜索算法(DPPLS)。DPPLS在分解的框架下,分别维持着两个种群,一个种群来保持解的收敛性,另一个用于贡献多样性。
1 概 述
1.1 多目标优化问题定义
一个多目标优化问题(MOP)的定义如下:
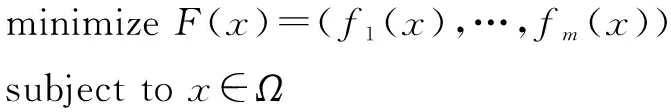
(1)
其中,Ω是决策空间;F:Ω→Rm是由m个实值目标函数组成的目标空间。可行目标域为{F(x)|x∈Ω}。当Ω为离散集合时,式1被称作一个多目标组合优化问题。
1.2 支配关系描述
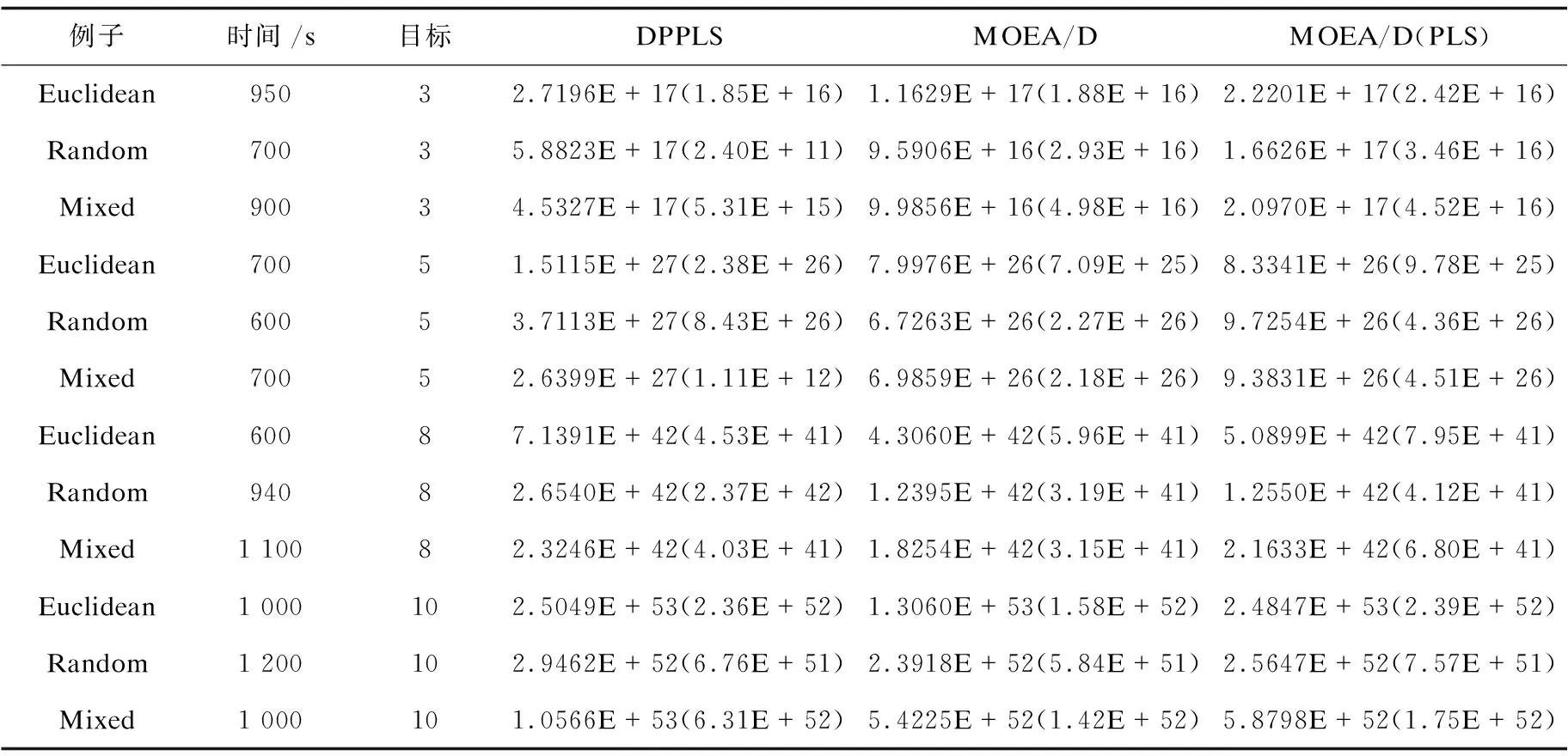
令u,v∈Rm,当且仅当对于所有的i∈{1,2,…,m}均有ui≤vi,且至少存在一个j∈{1,2,…,m}使得uj 在实际的多目标组合优化问题中,获得其PF通常是一个NP难问题。在过去的探索中,多目标启发式算法(如Pareto局部搜索[4-5]、多目标模拟退火等算法[6])、多目标元启发式算法(如多目标进化算法(MOEAs[7-13])以及多目标蚁群算法(MOACO[14]))被广泛应用于近似真实问题的PF。 在进化算法中,选择解的过程对算法效果及其重要。通常,算法的目的是获得收敛性和多样性取得权衡条件下的卓越的近似Pareto最优解集[15-16]。收敛性可以用来度量最终解解集合和真实PF的距离,其结果越小越好。多样性可以用来度量解集合在PF上分布的效果,其越均匀越好。基于上述两种选择解的需求,当前的进化算法可以分为基于指标的、基于分解的以及基于支配关系的算法[17-20]。一个基于分解的多目标进化算法的典型代表是MOEA/D[21],MOEA/D的核心思想是将一个多目标优化算法分解为多个子问题,然后同时优化这些子问题。这些子问题的目标函数可以是多目标优化问题线性或非线性的聚合函数。在MOEA/D中,每一个解都被绑定至一个子问题,并且如果两个子问题对应的权重向量之间的欧氏距离相近,则称这两个子问题为邻居。MOEA/D通过相邻子问题之间的相关关系来加速其搜索,通过在目标空间内进行多个方向的搜索来实现其多样性。 Pareto局部搜索(PLS)可以看作是单目标局部搜索的一个扩展[5],它通过一系列相互不支配的解来进行工作。Pareto局部搜索在每一迭代中,通过搜索这些非支配解的部分或者全部的邻居来进一步更新这个解集。当前,一个比较成功的PLS的变种是两阶段Pareto局部搜索(2PPLS)[5]。第一阶段通过聚合方法将多目标问题转化为单目标,然后对这些单目标问题利用现有的方法进行求解,产生一组高质量的非支配解集。第二阶段再利用Pareto局部搜索对第一阶段产生的解继续进行求解,往真实PF进行推进。最近,另外一种混合多目标启发式算法MOMAD[22],其结合了Pareto局部搜索和MOEA/D分解的方法在一些多目标组合优化问题中取得了优异的效果。 但是当前的2PPLS和MOMAD以及其他现存的多目标启发式算法并不适合解决3-目标或者3-目标以上的超多目标组合优化问题(CMaOPs[23])。主要原因如下[23-24]: (1)Pareto支配关系的效果急剧下降,这是因为随着目标个数的增加,解与解之间相互支配的概率会变得很低,大多数的解之间都是非支配关系。这也导致了一些常见的基于支配的算法在超过两个目标的组合优化问题上表现不佳。 (2)在MOMAD中,用来近似PF的解的数量没有很好的控制,因此极高的空间复杂度和时间复杂度限制了其在超过3个目标上的扩展。 文中算法主要基于MOEA/D算法框架,将一个多目标优化问题分解为N个单目标优化问题,一些聚合方法(权重和法、切比雪夫方法等)可以达到这些目的。在该算法中采用权重求和方法,工作原理如下: 对于权重向量W,有W={λ1,λ2,…,λN},其中 (2) 每一个分解后的单目标优化描述如下: (3) 在权重向量W中,λl是λk的T个最近的权重向量之一,则称λl是λk的邻居。第l个子问题也称为第k个子问题的邻居。 经过长期发展,Pareto局部搜索也有了很多的版本[22]。在这些版本和文中算法中,有一个重要的假设前提,就是在搜索空间里,通过定义正确的邻域关系,邻居可以通过从起始解集移动到邻居解集迭代生成。Pareto最优解集可以从邻居解集中获取。 每一次迭代中,在算法中保持两个解集: (1)工作集WP:WP={x1,x2,…,xN},其中xk是迄今为止在子问题k中通过聚合方法找到的最优解。 (2)外部集EP:外部集中的解都将进行Pareto局部搜索。 两个解集之间将一直进行通信,新解可以通过基因算子从工作集中生成,也可以通过在外部集中进行Pareto局部搜索生成。每一个新产生的解都有可能更新这两个种群。用来进行Pareto局部搜索的起始解集来自外部集,因为工作集通过基因算子生成的解可能会更新外部集,因此它可以帮助外部集跳出局部最优点。 算法1:主框架 输入:算法的终止条件;子问题的个数N;权重向量的集合W={λ1,λ2,…,λN};每个子问题的邻居大小T;一组标记向量S={s1,s2,…,sN} 输出:一组有效解集 /*初始化所有参数*/ /*对EP进行局部搜索*/ /*通过WP产生新解*/ if满足终止条件,停止并输出外部集,否则转到步骤2 在此阶段,工作集和外部集被初始化。由于已经将一个多目标问题分解成N个子问题,对于每一个k∈{1,2,…,N},都对应一个λk,在每一个子问题上应用一个单目标启发式方法来生成解xk,然后使用集合{x1,x2,…,xN}来初始化WP和EP。 算法2:初始化 输入:WP,EP,S,B 输出:WP,EP,S,B 对每一个k=1,2,…,N,在子问题k上应用一个单目标启发式方法来产生解xk,对应权重向量λk 初始化WP={x1,x2,…,xN},EP=WP 对于每一个si∈S,i=1,2,…,N,将si=false 计算每两个权重向量之间的欧氏距离,并获得每个权重向量最近的T个权重向量。对每一个i=1,2,…,N,设置B(i)={i1,i2,…,iT} 对于EP中的有效解,它的邻居也可能是有效的。基于这种假设,对EP中解x进行Pareto局部搜索来产生它的邻居集N(x),然后再使用N(x)来更新EP和WP。只有新加入的解才会被用来进行下一次的搜索。 算法3:Pareto局部搜索 输入:WP,EP,W,S,B 输出:WP,EP,S 对每一个xi∈EP以及si∈S,i=1,2,…,N,执行以下操作 ifsi==false,则 设置si=true /*N(x):解x的邻居*/ /*通过局部搜索产生新解*/ 对于每一个x'∈N(xi),执行: 设置I=B(i) 更新外部集EP(x'↓,EP,S,W↓,I↓) ifx'已经被加入到外部集EP 更新工作集WP(x'↓,WP,I↓); end end end end 算法4:生成子代 输入:WP,EP,W,S,B 输出:WP,EP,S; 对每一个i=1,2,…,N,执行以下操作 从B(i)中任意选择两个下标k,l,然后通过基因算子从xk和xl产生新解yi; 令I=B(i),更新外部集EP(yi↓,WP,I↓) ifyi可以被加入WP,则 令I={1,2,…,N}; 更新外部集EP(yi↓,WP,S,W↓,I↓) end end 在更新外部集EP时,输入的解y将会有两次比较。在第一阶段,y将比较EP中的一些解,并且替换掉被y支配掉的解。如果y被其中任意一个解所支配,该过程将结束。如果y没有被任何所选的解支配,则进入第二阶段。第二阶段通过一种新的方法比较之前的解。对所有j∈I,第j个子问题对应解xj和参考线λj。计算解y与λj之间的角度θ1以及xj与λj之间的角度θ2,如果θ1<θ2,则解y替换解xj。 外部集的更新在算法的第三步和第四步都会更新。对外部集EP中的解进行Pareto局部搜索,每一个通过基因算子新产生的解x的邻居如果能够加入工作集WP则更新外部集EP。假设Pareto局部搜索产生的邻居距离原始解很近,因此可以仅更新EP中该解的邻居。如果解是通过基因算子产生的,应该更新整个外部集。 算法5:更新外部集EP 输入:y,EP,S,W,I; 输出:EP,S; 对每一个xi∈EP并且i∈I,执行以下操作 ify被xi所支配,则 return end ify支配xi,则 使得xi=y且si=false end 对于每一个xj∈EP并且j∈I,执行以下操作 θ1=angle(y,λj) θ2=angle(xj,λj) ifθ1<θ2,则 设置使得xi=y且si=false end end 当一个新解通过基因算子或者Pareto局部搜索产生时,也会更新工作集WP。在算法4中,解y是子问题i产生的新解,I是子问题i所有邻居的索引集合。对I中的每一个k,如果解y的聚合函数值更优,则y将会替换解xk。 算法6:更新工作集WP 输入:y,WP,I 输出:WP 对每一个xk∈WP(k∈I),执行以下:ifgws(y|λk)≤gws(xk|λk),则 设置xk=y end end 为了验证提出的算法,选择经典的多目标旅行商问题(mTSP)进行对比分析。 多目标旅行商问题(mTSP)是一个经典的NP-难的多目标组合优化问题。对于一个无向图G=(V,E),其中V={1,2,…,N}是城市集,E={e=(i,j)|i,j∈V}是边集。对于每一条边e有m个距离度量指标de,1,de,2,…,de,m。一个可行解是一个所有V元素的全排列组合,同时也是一个所有边E的哈密顿回路。对于mTSP的第i个目标,算法的目的是最小化以下函数: (4) 其中,x为E的子集形成的解。 生成了5~10目标的测试实例,并且考虑以下三种类型的实例: (1)欧氏距离测试集(Euclidean):假设所有的节点分布在一个平面上,两个城市之间的边的成本是对应均匀分布的; (2)随机测试集(random):每条边的成本是通过均匀分布随机生成的; (3)混合测试集(mixed):这种实例是(1)和(2)的混合,一部分是欧氏实例,另一部分是随机实例。 算法中工作集WP和外部集EP(N)的大小是相同的。过大的种群将会导致每一代都有很高的计算复杂度,过小的种群又会导致搜索丢失PF的一部分。基于这些考虑,N的设置如下:3目标时设置N=300,5目标时设置N=210,8目标时设置N=156,10目标时设置N=275。每一个子问题的邻居集大小设置为20,且所有测试用例独立运行30次。 采用最常使用的性能评估指标:HyperVolume(IH)[25],其值越大表示结果越好。 (1)第一步中的工作集WP和外部集EP:因为将多目标优化问题分解成N个子问题,利用随机方法来生成解xk。设置WP={x1,x2,…,xN},以及EP=WP。 (2)解x产生的邻居解集N(x)(算法3的第4行):Pareto局部搜索的重要步骤是如何通过解x产生它的邻居解集N(x)。算法中的邻居使用了文献[22]中提供的2-opt方法。 (3)工作集WP交叉变异算子:文中使用GoldBerg和Linge提出的PMX交叉和单交换变异来产生新解。因为在很多问题上PMX交叉算子[26]比其他交叉算子的效果更好。 由于在目标个数上升到3或者更多的时候,现有算法如MOMAD等无法解决该类超多目标问题。因此,在3~10个目标的mTSP问题中,使用MOEA/D算法进行比较。对于这两种算法,同样的PMX交叉和单交换变异策略被用来产生新解。由于这两种算法只保持一个种群并且使用基因算子来产生新解,因此添加了Pareto局部搜索到原始的MOEA/D算法中作为一个补充,来实现公平的比较,命名为MOEA/D(PLS)。 实验中,这些算法都是基于C++编码,并且使用了同样的CPU时间,所有的实验都是基于一台Intel 2.6 GHz,8 GB内存的PC实现。 实验比较了在相同运行时间下HyperVolume在不同问题实例下的值。从表1可以看出,DPPLS的性能要好于其余两种比较算法。DPPLS作为MOEA/D算法框架的一个拓展,其在超多目标上的效果要好于MOEA/D本身。此外,使用Pareto局部搜索策略的MOEA/D算法效果也要优于通过普通的交叉变异生成解的方式。 表1 MOEA/D-PLS和MOEA/D在测试问题上HyperVolume的比较 针对现有的多目标组合优化算法无法较好地解决目标数大于3的超多目标组合优化问题,提出了一种多目标组合优化算法。在基于MOEA/D算法的框架下,利用两个种群,其中一个作为工作集来运作MOEA/D,另一个用于进行Pareto局部搜索。实验结果表明,该算法相比较MOEA/D而言,在超多目标问题上具有很好的效果。1.3 多目标组合优化问题
1.4 进化算法背景
2 算 法
2.1 主要框架
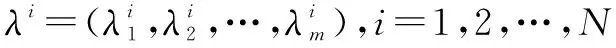
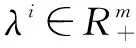
2.2 初始化
2.3 EP(外部集)的Pareto局部搜索
2.4 EP(外部集)的更新
2.5 WP(工作集)的更新
3 实 验
3.1 多目标旅行商问题(mTSP)简介
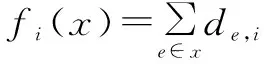
3.2 测试问题
3.3 实验参数设置和度量指标
3.4 算法设置
3.5 比较算法
3.6 实验结果
4 结束语

