基于用户兴趣和项目分类的协同过滤推荐算法

丛洪杰，龚 安，李华昱，帅训波

(1.中国石油大学(华东) 计算机与通信工程学院，山东 青岛 266580； 2.中国石油勘探开发研究院 计算机应用技术研究所，北京 100083)

0 引 言

互联网和移动互联网的蓬勃发展，带来了信息快速增长，在海量数据中获取对自己有价值的信息更加困难，个性化推荐算法成为解决这一问题最有效的技术之一[1]。在个性化推荐算法中，协同过滤推荐在工业界和学术界都取得了很大的成功[2]。

随着大数据时代的来临，协同过滤的弊端也越发突出，包括数据稀疏性、冷启动、可扩展性差、小规模数据离线处理算法无法应用到大规模数据处理等[3]。针对这些问题，学者们提出了许多解决办法。邓爱林等[4]为减小数据稀疏性带来的推荐精度低的问题，提出了一种基于项目评分预测填充空缺值的方法，然后采用一种新颖的相似性度量获得目标用户更加准确的最近邻居，使得推荐质量有所提升。Melville P等[5]在缓解评分数据的稀疏性方面，则采用基于内容的方法预填充用户评分矩阵中的未评分项，从而提高推荐精度。

韦素云等[6]考虑了项目类别和兴趣度等因素，提出一种改进的协同过滤推荐算法。该算法首先计算项目之间的类别距，然后结合项目类别信息，考虑不同项目之间的相关程度，构造出项目类别相似性矩阵，衡量项目间相似性的标准采用改进的条件概率的方法。孟祥武等[7]提出大数据时代的推荐系统，充分利用丰富的用户反馈、社会化网络等信息进一步提高推荐系统的性能和用户满意度。国琳等[8]提出通过构建和分析用户兴趣分布曲线以发现兴趣领域专家，并甄别状态不正常的伪专家。

王立才等[9]提出上下文感知的推荐系统，利用上下文信息，改善推荐系统的推荐精确度和用户满意度，从面向过程的角度论述了上下文感知推荐系统的研究进展和难点。刘平峰等[10]提出用户兴趣图谱，建立兴趣领域本体，集成兴趣图谱的动态性，实现用户兴趣匹配与定位，进而提高推荐系统的精度。Pessemier T D等[11]提出个性化的混合推荐模型，该模型更多考虑了用户的偏好、约束限制和用户反馈等因素，使得推荐个人旅行线路更加符合用户兴趣。Oh J等[12]提出一种个性化流行趋势匹配算法，计算目标用户的个性化趋势，匹配用户兴趣偏好，提升预测评分，产生更加精准的推荐列表。

以上所述研究虽然对推荐算法做出了改进，并且取得了不错的效果，但对于项目类别和用户兴趣没有加以充分挖掘利用。对此，文中算法引入用户兴趣分布预测填充评分矩阵空缺值，缓解数据稀疏性，改进相似性度量方法计算项目相似性，以减小预测评分的误差。

1 项目分类

1.1 评分矩阵

基于项目的协同过滤算法中，计算项目的相似性是关键步骤。项目类别数据和用户评分数据为文中推荐算法的基础数据，由此可构建项目类别分布矩阵、用户兴趣分布矩阵和用户评分矩阵。

(1)项目类别分布矩阵。

项目类别分布矩阵由n×k的矩阵C(n,k)表示，如表1所示，其中n为项目的个数，k为项目类别的个数。

(2)用户兴趣分布矩阵。

用户兴趣分布矩阵由m×k矩阵D(m,k)表示，见表2，其中m为用户的数目，k为用户兴趣种类数。

表1 项目类别分布矩阵C(n,k)

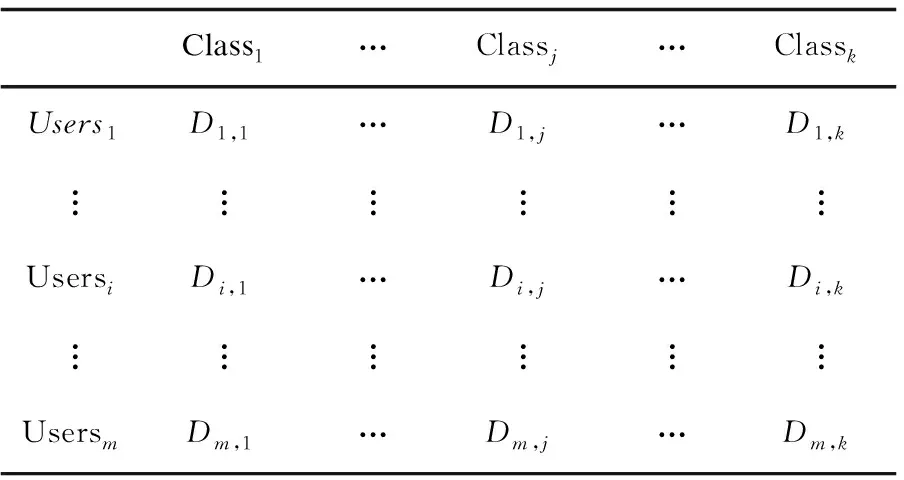
表2 用户兴趣分布矩阵D(m,k)

(3)用户评分矩阵。

用户评分矩阵由m×n的矩阵R(m,n)表示，见表3，其中用户数目用m表示，项目数目用n表示，Ri,j表示用户i对项目j的评分。

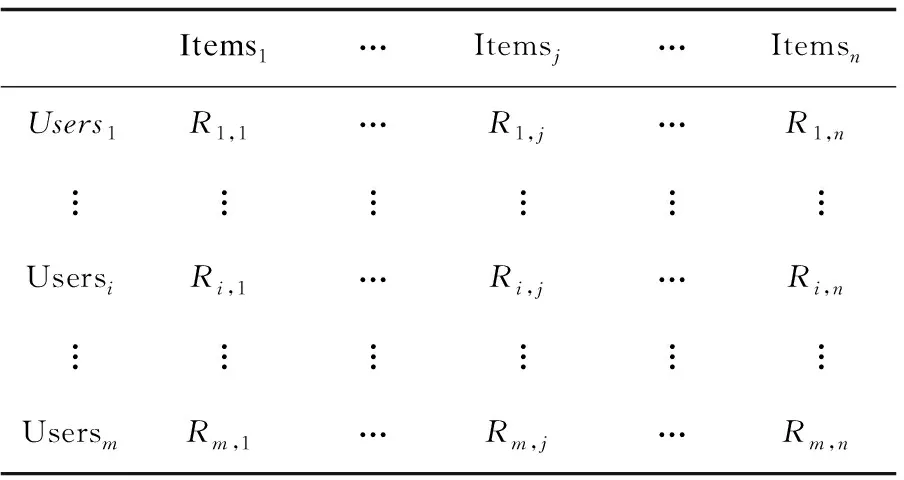
表3 用户评分矩阵R(m,n)

1.2 相似性度量方法

传统的基于邻域的协同过滤算法，度量用户或项目间的相似性是关键的一步。以下是计算项目之间相似性主要采用的三种方法：

(1)余弦相似性(cosine similarity)：把项目看作m维用户的空间向量。设向量i和向量j分别代表用户对项目i和项目j的评分，则项目i和项目j之间的相似性sim(i,j)定义如下：

(1)

其中，Ru,i、Ru,j分别为用户u对项目i和项目j的评分；U表示用户对项目i和项目j都有评分的用户集合。

(2)皮尔森系数(Pearson correlation)。

(2)

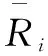
(3)修正余弦相似性(adjusted cosine similarity)。

(3)

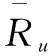
2 基于项目分类的修正余弦相似性

用户规模和项目数目的增加，使得评分矩阵的数据稀疏性逐渐增加，从而导致预测评分精度低。目前解决办法就是对用户未评分项进行预填充，固定缺省值是最简单且常用的方法之一，该方法可以有效地提高系统的推荐精度。但实际生活中评分矩阵中的缺省值显然不可能都一样，因此填充固定缺省值的方法没有从根本上解决数据稀疏性问题。文中以用户兴趣分布评分矩阵求相似用户，对空缺值进行预测填充，减小用户评分数据的稀疏性。

传统的修正余弦相似性的度量方法是对用户的评分去中心化，通过减去用户的平均评分，改善了用户评分尺度不同的问题。评分尺度问题主要由用户评分的标准不同而导致，比如评分区间为1～5分时，用户对于项目评分A可能是3分以上喜欢，而B则4分以上才为喜欢。但是上述方法仅仅考虑了用户评分尺度问题，对于项目的类别用户的评分标准也是有所不同的，比如用户对动作类或科幻类的电影更加偏好，那么用户会普遍给这一类别的电影更高的评分。文中提出对项目进行分类，计算用户在项目的每种类别中的评分标准，以此来改进计算项目相似性的过程，以寻找更加准确的K近邻。

2.1 用户兴趣分布填充空缺值

基于项目的协同过滤，主要由计算项目的相似邻居，预测目标用户对项目的评分和生成推荐列表等过程组成，其中计算项目的相似邻居需要用户对项目i、j同时具有评分。求用户对项目i和对项目j分别有评分的并集公式表示为：

U=Ui∪Uj

(4)

其中，U表示所有用户的集合；Ui和Uj分别表示对项目i和项目j有过评分的用户集合。

对用户集合中分别对项目i、j未评分的项进行填充预测评分，定义P{pu,i,pu,j,…}。

预测填充策略，本阶段采用用户兴趣分布矩阵作为求最近邻居的输入数据，通过基于用户的协同过滤算法进行预测评分。

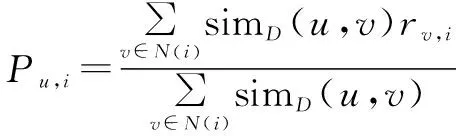
(5)

其中，Pu,i为预测评分；simD(u,v)为用户u和用户v通过用户兴趣分布矩阵求得的相似度；rv,i为相似用户对项目i的评分。

2.2 项目分类修正余弦相似性

sim(i,j)=

(6)

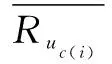
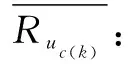
(7)

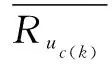
2.3 算法描述

输入：用户的项目评分矩阵R，项目类别信息，项目集合Items，目标用户集合U，项目邻居数目K，推荐列表长度N

输出：目标用户u对项目的预测评分，且生成目标用户u的推荐列表

(1)根据数据集中项目分类信息构建项目类别分布矩阵C(n,k)；

(2)根据项目分类信息和用户项目评分矩阵R，计算用户兴趣分布矩阵D(m,k)；

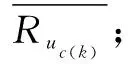
(4)求用户对项目i和项目j分别有评分的用户的并集；

(5)对并集中用户对项目i或项目j未评分项，采用用户兴趣分布的协同过滤算法进行预填充值；

(6)构建用户项目评分矩阵，求得项目i和项目j有着共同评分的用户集U；

(7)利用基于项目分类的修正余弦相似性来计算项目之间的相似度，生成相似度最大的k个项目邻居；

(8)通过求得的相似邻居和相似度值来预测目标用户对项目的评分；

(9)通过对预测评分的排序，推荐top N项目给目标用户。

3 实验结果与分析

3.1 实验数据集

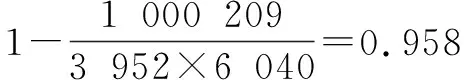
3.2 评价指标

实验采用平均绝对误差(mean absolute error，MAE)来评价算法的推荐精度[13]。假定目标用户的预测评分集为P{p1,p2,…,pn}，与其对应测试集中的真实评分集为Q{q1,q2,…,qn}，则MAE表示为：

(8)

3.3 实验方案

首先对数据进行预处理，构建用户的兴趣分布数据以及项目分类数据，然后使用Java编程语言对推荐算法进行实现，分别对传统的余弦相似性、修正余弦、改进的修正余弦进行实现，对目标用户和电影进行预测评分，评估推荐精度；最后对比文中算法与其他两种算法的推荐精度。

3.4 实验结果分析

为了验证算法的有效性，在使用相同数据集规模及验证方法上，对传统协同过滤算法中使用的余弦相似性、修正余弦相似性的相似性度量方法与文中提出的改进修正余弦相似性进行实验对比。最近邻居的规模从10到100递增，实验结果如图1所示。

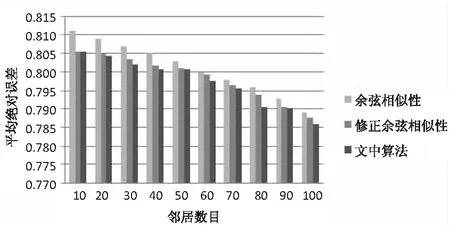
图1 推荐算法的MAE值比对

从图1可以看出，文中提出的方法随着最近邻居的增加MAE值逐渐减小，且低于传统协同过滤方法。因为文中方法考虑了项目的类别以及对于用户兴趣分布的因素，在此基础上计算的用户的最近邻居相似度更加符合现实，更加准确，而通过更加准确的最近邻居用户群体，可以获得更加符合目标用户的预测评分。所以该算法可以有效提升推荐质量，为用户提供满意的个性化推荐列表。

4 结束语

针对协同过滤算法所面临的数据稀疏性、推荐精度低等[14]问题，采用了基于用户兴趣分布方法初步填充评分矩阵中的未评分项；在计算项目相似性阶段，提出一种基于项目分类改进修正余弦相似性度量方法，即由用户平均评分去中心化的方法改为对用户兴趣类别平均分去中心化，求出最近邻居并生成推荐列表。实验结果表明，该方法具有较小的MAE，在一定程度上提高了推荐质量。