一种基于旋转不变性的纹理粗糙度改进算法

张芝齐，吴建平,2,3，钱文华，陈培德,2,3

(1.云南大学 信息学院，云南 昆明 650500； 2.云南大学 云南省电子计算中心，云南 昆明 650223； 3.云南省高校数字媒体技术重点实验室，云南 昆明 650223)

0 引 言

纹理是图像表面的一种固有属性，与其他的图像特征不同，虽然目前对纹理尚无正式准确的定义，但一般而言，如果一幅图像在局部区域表现为不规则性，但在图像的整体性上又表现为规律性，就将这幅图像所具有的这种图像特性称为纹理[1]。纹理特征作为所有图像固有的属性，尤为重要。Tamura等[2]提出了构成纹理视觉模型的6个纹理属性，分别是粗糙度、对比度、方向度、线性度、规则度和粗略度。而粗糙度是最重要、最基本的纹理特征[3]。从狭义的观点来看，纹理就是粗糙度[4]。

在少数民族图案中同样存在着各种各样的纹理基元，许多科研工作者正致力于这些图案纹理特征的研究和分析，而最首要的就是纹理粗糙度，因此这些少数民族图案中的纹理粗糙度的数字化为图案纹理特征的研究和分析提供一种新的方式，同时也能更客观真实地表达这些少数民族图案的深刻内涵并提供相应的数据支撑。记载和传承这些少数民族图案的纹理特征，最重要的就是对粗糙度的数学表达。Rosenfeld提出了最佳尺寸纹理粗糙度算法，该算法不但可以有效处理显微纹理图像，而且能克服粗糙度对对比度的依赖性[5]。

但是，通过分析仍然能够发现该算法的不足之处。从该算法的计算过程中可以发现，在计算领域均值差值时会丢掉相当一部分图像信息，因此在不同角度对图像提取纹理粗糙度时其旋转不变性必然会受到影响，同时在选取最佳尺寸时的量化精度还不是最优。因此，文中主要基于旋转不变性对该算法进行改进，提出了一种新的领域均值差值的计算方法和一种新的量化方式。

1 Rosenfeld纹理粗糙度算法

Rosenfeld提出的基于最佳尺寸[6]的纹理粗糙度算法是一种经典的纹理粗糙度算法，其计算结果较为符合人眼的视觉感受。

下面对其计算过程作如下介绍：

步骤一：对每一个像素，计算多尺寸领域均值。选取领域尺寸为2的幂次方，如2×2，…，32×32。采用的领域尺寸为2的幂次方加一，即(2k+1)×(2k+1)，其中k≥1，像素的领域均值为：

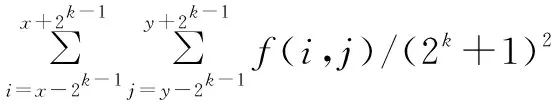
(1)

其中，f(i,j)为像素(i,j)的灰度值。

步骤二：对每一个像素，计算在水平方向和垂直方向上关于当前像素对称的领域边缘像素的2个领域均值差值。计算公式分别为：

水平方向：

Ek,h(x,y)=|Ak(x+2k-1,y)-Ak(x-2k-1,y)|

(2)

垂直方向：

Ek,v(x,y)=|Ak(x,y+2k-1)-Ak(x,y-2k-1)|

(3)

取水平和垂直两方向上的最大均值差值为当前像素的领域均值差值。

Ek(x,y)=max(Ek,h(x,y),Ek,v(x,y))

(4)

步骤三：对每一个像素，从多领域尺寸中确定一个最佳尺寸。

Sbest(x,y)=2k+1

(5)

使得

Ek=Emax=max(E1,E2,…,EL)

(6)

其中，E为领域均值差值；L为领域尺寸个数，即为k。

步骤四：计算最佳尺寸Sbest的平均值，作为灰度图像的纹理粗糙度。

(7)

2 原纹理粗糙度算法的改进

2.1 领域均值差值的改进

从上述Rosenfeld纹理粗糙度计算过程中不难发现，步骤二中在计算某点的领域均值差值时其实只用到了关于该点对称的两个点的像素，其领域范围内的其他点都没有用到，这必然会忽略图像的一些信息。因此，针对上述算法中计算领域均值差值的缺陷性，提出了如下改进。

重新计算水平和垂直方向的领域均值差值，具体过程如下：

水平方向：

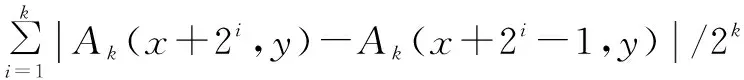
(8)

如式1所示，在(2k+1)×(2k+1)的尺寸范围内，水平方向上相邻像素灰度值依次作差后取绝对值，则在上述尺寸范围内为2k-1组个差值，将这2k-1组个差值求和，然后再对其求平均作为新的水平方向的领域均值差值。

同理，垂直方向：

(9)

将上述得到的水平和垂直方向的领域均值差值转入原Rosenfeld纹理粗糙度算法继续进行计算。

2.2 尺寸量化精度的提高

一般来说，Rosenfeld算法有两种量化方式来选取领域尺寸，分别是指数量化和线性量化。原Rosenfeld纹理粗糙度算法是根据从不同尺寸中领域均值最大准则来确定最佳尺寸，然后其采用的是指数量化来选取领域尺寸[7]。后面，相继有专家学者提出线性量化[1,4-5]来改进原有的量化方式，使其量化精度得到提高。而文中提出一种分式量化，使其量化精度进一步提高，下面从理论上加以论证。

(1)给出三种量化方式的数学表达。

指数量化：

SE(n)=Mn+1

(10)

线性量化：

SL(n)=M×n+1

(11)

分式量化：

(12)

其中，n≥1,M≥2。

(2)三种量化方式的精度为：

指数量化精度：

ΔSE(n)=SE(n+1)-SE(n)=Mn+1-Mn=

Mn(M-1)

(13)

线性量化精度：

ΔSL(n)=SL(n+1)-SL(n)=M×(n+1)-

M×n=M

(14)

分式量化精度：

(15)

所以，令C=M-1≥1，则

ΔSE(n)-ΔSL(n)=(M-1)Mn-M=M[(M-

1)Mn-1-1]=M[CMn-1-1]

(16)

从上述分析中看出，分式量化的精度要高于线性量化，线性量化要高于指数量化。

3 旋转不变性实验

3.1 Brodatz纹理图像库的实验分析

Brodatz[8-10]纹理图像库作为一种标准的纹理图像库，其实验结果具有较高的实验验证价值。将D1-D100

这100张图片分别用原Rosenfeld纹理粗糙度算法和改进后的Rosenfeld纹理粗糙度算法[11-13]进行测试，对这些图像从0度到90度每间隔5度进行旋转，则一共为19个角度。为了防止旋转产生的黑边对实验结果产生的影响，将以每幅图像的中心进行图像的截取，最后形成181×181的实验图像进行旋转不变性验证实验，并用每幅图像19个角度所计算出的纹理粗糙度的方差来衡量算法的旋转不变性的性能。结果显示，用原算法得到的方差均远大于改进后算法得到的方差，原算法最大方差为5.018，方差大于1的多达22幅图像，平均方差为0.658；而改进后算法的最大方差为1.657，方差大于1的仅1幅图像，平均方差为0.153。从上述数据显示，改进算法的旋转不变性得到了显著增强。

下面选取其中十张(D7、D38、D44、D60、D68、D77、D85、D88、D89、D92)从0度到90度每间隔15度进行旋转(共7个角度)并编号为P1-P10(如图1所示)，大小为181×181有代表性的图像进行阐释。

图1 实验图像P1-P10

计算结果如表1和表2所示。

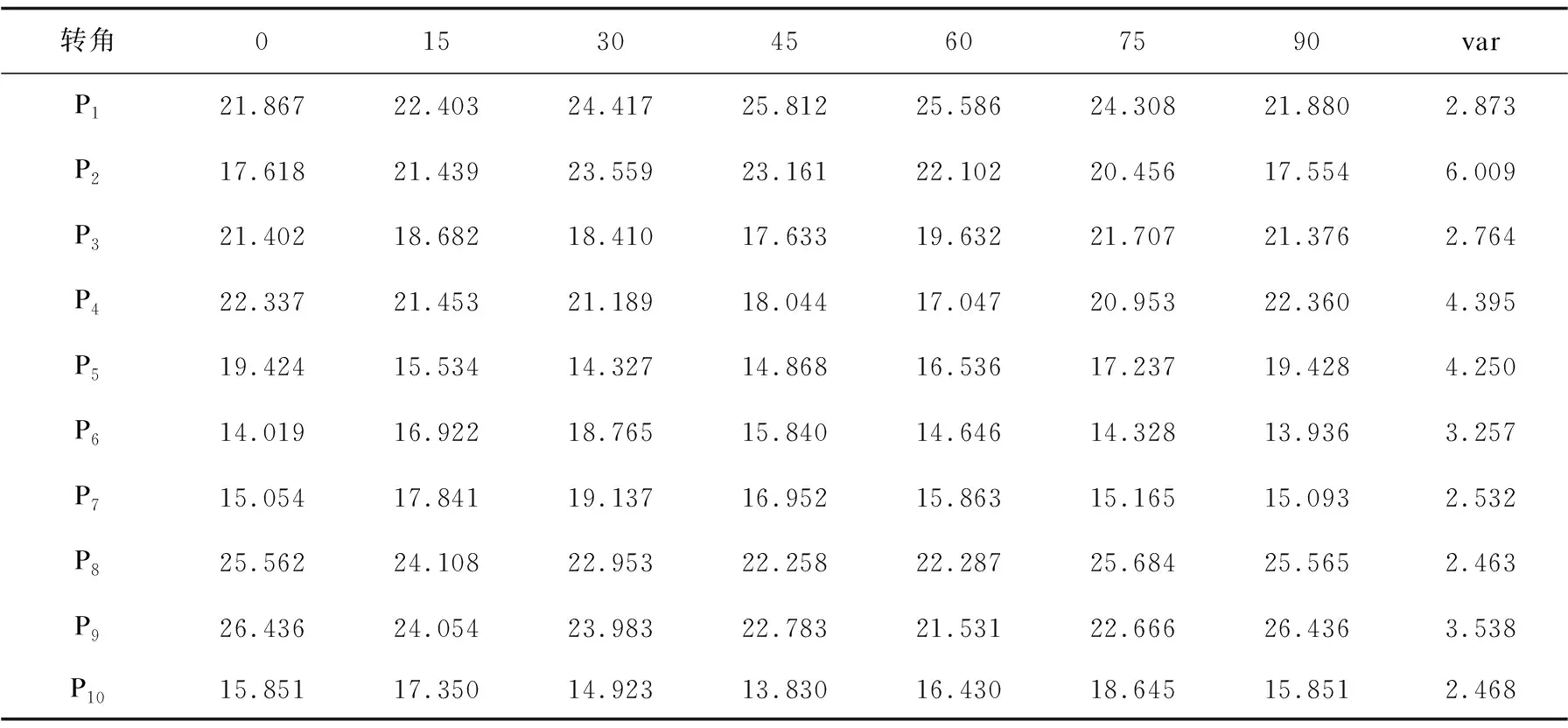
表1 原Rosenfeld算法的粗糙度Brodatz纹理图像计算结果

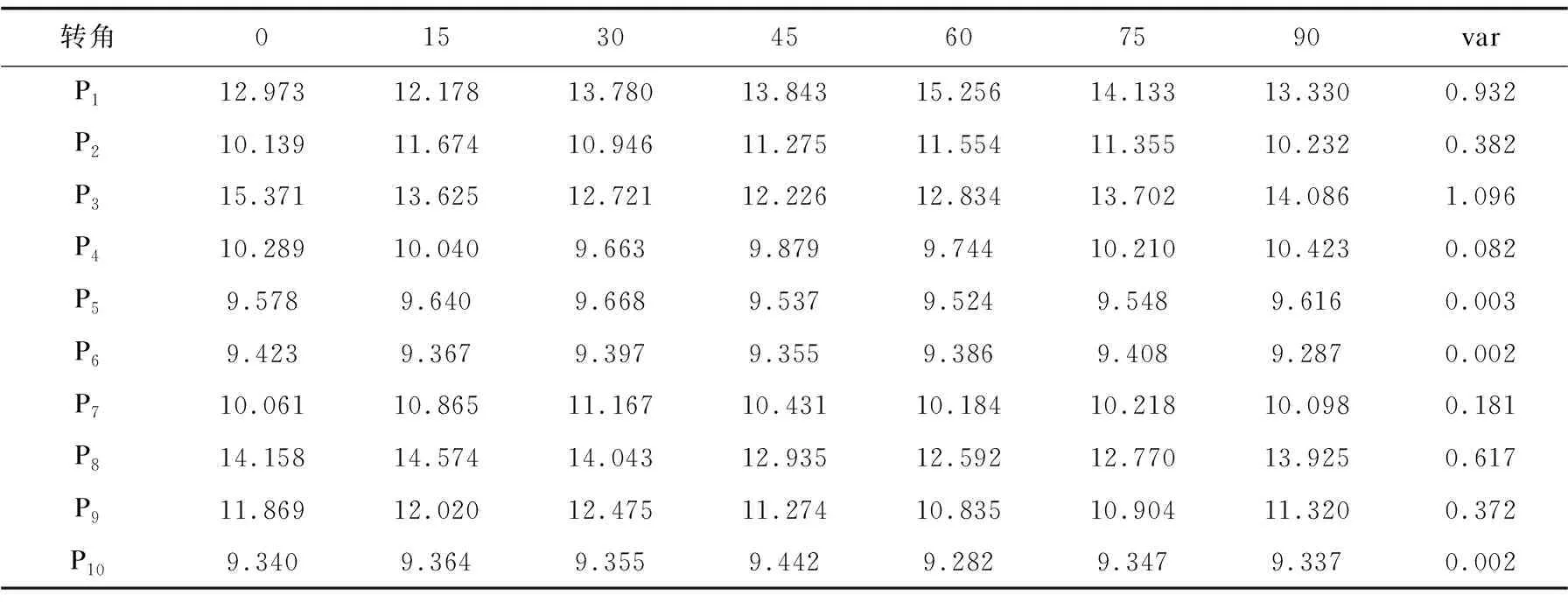
表2 改进后算法的粗糙度Brodatz纹理图像计算结果

从表1、表2可以看出，使用改进后的纹理粗糙度算法得到的结果在不同的角度更稳定，即旋转不变性得到了改进。

3.2 苗族刺绣图案的实验分析

苗族刺绣图案作为少数民族重要的历史文化遗产，对其图案纹理特征，尤其是纹理粗糙度的提取对于少数民族图案的检索和分类[14-15]有着重要的意义。同时，通过提取的这些纹理粗糙度可以数字化地记载少数民族图案的符号特征，为更准确有效地分析少数民族图案的特征提供了有力的数据支撑，对少数民族文化的研究也具有十分重要的意义。下面通过4幅具有

代表性的苗族刺绣图案(mi1-mi4)进行描述(见图2)。同样地，对这4幅苗族刺绣从0度到90度每间隔15度进行旋转(共7个角度)，其大小也为181×181并灰度化，通过实验进一步验证改进后算法的旋转不变性得到增强。

图2 苗族刺绣图案mi1-mi4

计算结果如表3和表4所示。

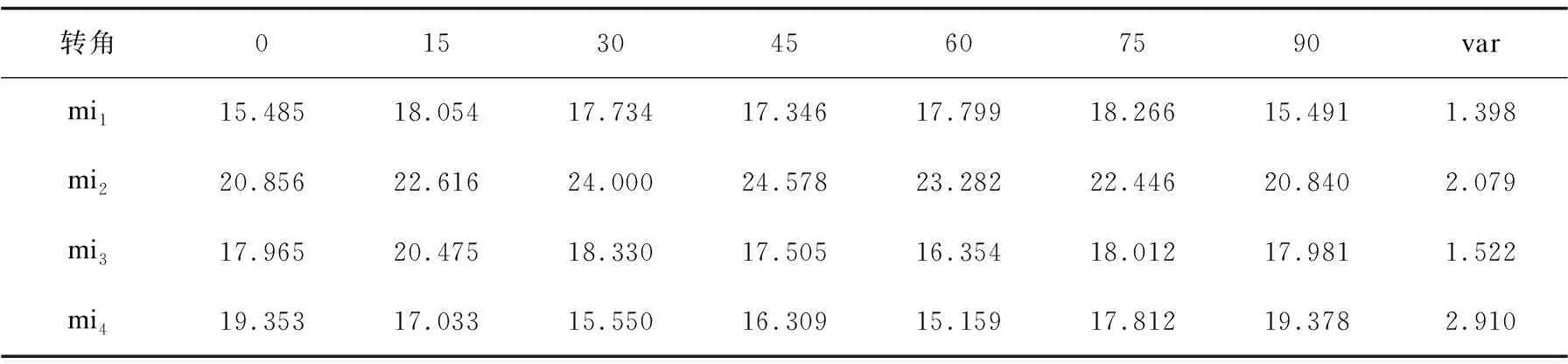
表3 原Rosenfeld算法的粗糙度苗族刺绣图案计算结果

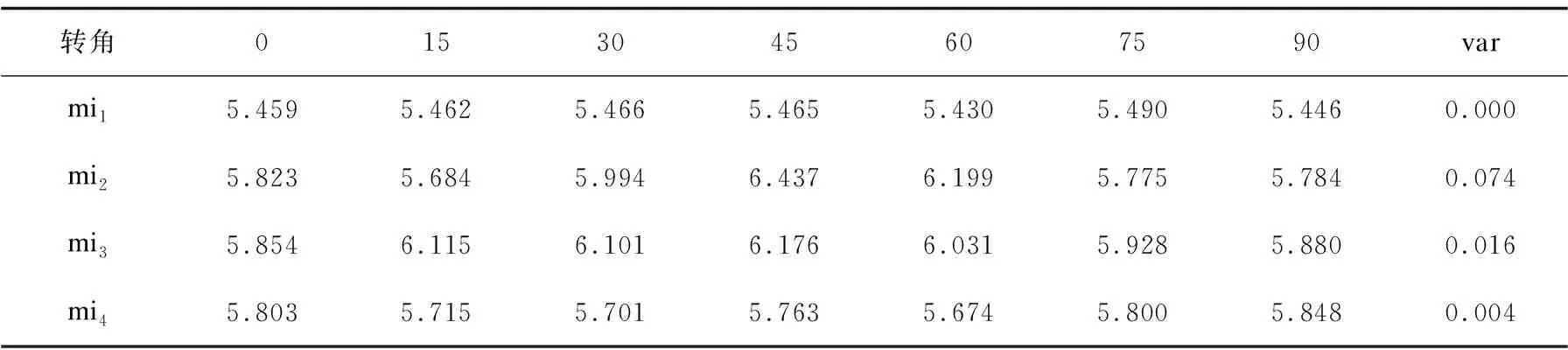
表4 改进算法的粗糙度苗族刺绣图案计算结果

从表3和表4的测试结果中不难得出，改进算法对不同角度提取纹理粗糙度有更强的适应能力，在保留小数点后三位的情况下，对mi1这一图案的纹理粗糙的提取结果的方差可以直接为0，从实际的应用图案中也可以进一步说明改进算法的旋转不变性更强。

4 结束语

从计算领域均值差值和尺寸量化方式改进了原Rosenfeld纹理粗糙度算法的旋转不变性和量化精度，并通过Matlab实验进行了相关数据的论证，证实了改进算法的旋转不变性确实得到了提高。通过少数民族图案中苗族刺绣的纹理粗糙度在不同角度的提取具有很高的旋转不变性，能够客观精确地表达相应的图案纹理特征，为少数民族图案纹理特征的研究提供了良好的技术支持，对少数民族图案这一历史文化遗产的

传承和发扬提供了一种有效的记载方式。下一步可以针对少数民族图案保存中图案的失真度较高和图案的记载信息庞大这一现状，通过对算法的抗噪性能及运算效率加以改进和提高来适应实际工程的应用。