取舍•整合•挖掘—论小学数学课堂练习的设计
徐晓燕
(浙江省景宁畲族自治县民族小学,浙江丽水 323000)
引 言
我们一般分三个层次进行习题设计。习题分层如下:第一层次是基本的、单项的、模仿性的或稍有变化的练习,侧重知识的内化——落实习题的教育、教学、检查等功能;第二层次是变式的、对比的、灵活性的练习,侧重将知识转化为技能——落实习题的发展功能;第三层次是思考性的、综合性的、发展性的练习,侧重知识的深化与优化——落实习题的发展、开放等功能。“轻负高质”的教学呼唤高效的作业,要求教师能根据教学目标,精心选择、设计针对性强的练习。那如何设计出高效的作业呢?笔者以《连乘解决问题》一课为例,对习题设计展开分析,对这节课的练习设计,进行取舍、整合、挖掘,最大化发挥这道题的作用。
一、取舍合理,突出实效,体现作业的针对性
既舍重复相似的多个练习,也舍脱离学生实际生活和社会生活的习题,而取学生熟悉的学校环境为素材(见表1)。

表1
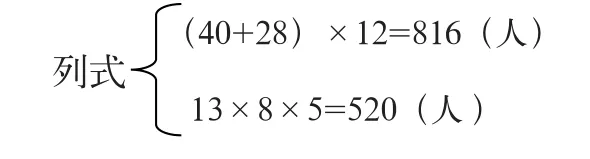
通过比较体验、完善认知结构,注重解构。防止学生套用模式,以为今天的问题都是用连乘来解决的,而不去分析、理解。教材中的练习都较注重给学生建立良好的连乘模型,很多题目都是用建立的连乘模型来解决的,没有进行解构。这样安排可能会对学生造成一定的思维定势,该怎样打破?对刚建构的模型怎样去解构?于是我想尝试通过以上一组连乘与乘加题目的比较,让学生进一步了解连乘问题的结构特点,对于连乘的理解不再只停留在对方法的比较上,而能充分与运算意义结合起来,以加深学生对连乘问题的理解。我们只有根据自己课堂的教学目标及学生的学情进行科学的取舍,才能使数学课堂在“舍”中“取”得。
二、整合材料,追求简约,体现作业的高效性
设计数学习题时,根据基本题的特点,适当变换条件和问题,使之层层深入,环环相扣,达到一题多用的目的。这样既能提高练习效率,又可培养学生思维的深刻性和广阔性。
变式前:小红每天跑两圈,每圈400米,小红7天共跑了多少米?
可以列 式400×2×7=5600(米),也可列式2×7×400=5600(米),并要求说出先算出什么,再算出什么。
变式后:(改变条件,问题不变)小刚每天跑400米,小红每天跑的是小刚的2倍,小红7天共跑了多少米?
列式:400×2×7=5600(米)
先出现问题,想解决问题的条件,解决了问题后改变原有信息进行对比,从对比中知道虽然条件转换了,但要算出“小红7天共跑了多少米?”先要算出“小红一天跑多少米?”变式前的题型完全和上面的例题一致,是连乘应用题建立模型后的完全模仿和巩固。而变式后的练习可以拓宽这个模型的外延,可以使一个学习材料反复使用、深化拓展、比较利用,力求做到“低投入(教学成本),高产出(课堂效益)”。把习题的检测功能和发展功能统一体现在一组题中。
三、挖掘充分,提高思维含金量,体现作业的探究性
使用练习时要注意充分挖掘练习的价值,充分发挥练习的功能,防止发生走过场的现象,要着重于练习题在“质”上的提高,要使学生练习一题就有一题的收获,甚至一道好题当作十题来练,使学生可以从中悟出数学思想,达到举一反三、触类旁通的功效。练习的设计不能仅仅局限于一个问题的解决,还要关注学生在解决这个问题中自主领悟到的数学知识及思想、方法,关注解决问题过程中数学素养的形成。
如拓展解决综合性问题(如图1所示)

图1
请问将这些邮票全部买下需要多少钱?
方法一:(5×9-1)×80=3520分=352角:
方法二:(5×8+4)×80=3520分=352角;
方法三:5×9×80-80=3520分=352角;
.......
让学生自主解决问题后,反馈各种方法,将先求出“共有几张邮票”的归一类,再讨论对5×9×80-80的理解。让学生感悟到本课连乘问题在题目中的应用。接着笔者再挖掘本题,把课件动态变式为:卖了一些后(如图2),买剩下的邮票需要多少钱?
先求邮票的张数,再求需要多少钱?求张数:
方法一:1+3+5+7+9 =25(张);
方法二:5+4×2+3×2+2×2+2=25(张);
方法三:5×5=25(张)。
先反馈学生用1+3+5+7+9求出邮票张数,再求需要多少钱的方法后问:“你还有其他方法吗?”“你有更简便的方法吗?”在学生的讨论中一步一步地引出移一移的办法可以列式为:5×5×80来解决。再问:“你是怎么移的?”“你是怎么想到这样移的?”从中渗透了移多补少的数学思想,又一次进行了数形结合。提升了本题的思维含金量,让课堂充满了数学趣味。
从上面的练习安排中我们可以发现,它打破了原来单纯的图文结合单一的题目呈现方式。有图文结合的、有纯图的、也有纯文字的,还有通过连乘算式寻找生活原型的,这些练习题在两步连乘的背景下,在多种呈现方式下,使学生能更好地理解连乘的模型。同样也打破了习题呈现相对单一的状况,并做了有机的整合,在丰富形式的练习中,让学生可以更清晰地去理解数量关系。
结 语
综上所述,练习设计的过程就是取舍、整合、挖掘的过程。当然,这里的取舍、整合、挖掘都不是相互独立的,而是一个相辅相成的过程。

