基于LMD与随机森林的滚动轴承故障诊断

秦喜文， 郭 宇， 郭佳静， 董小刚，冯阳洋， 王强进

(1.长春工业大学 数学与统计学院， 吉林 长春 130012;2.长春工业大学 汽车工程研究院， 吉林 长春 130012)

0 引 言

滚动轴承故障诊断过程主要包括故障特征提取和分类，其本质是模式识别的过程[1]。机械设备一旦发生故障，不但会消耗大量的维修时间和维修费用，而且会给企业带来巨大的经济损失[2]。因此滚动轴承的状态监测和故障诊断都有非常重要的研究意义。

滚动轴承故障振动信号多数为非平稳信号，所以在故障诊断中必须运用可以处理非平稳信号的特征提取方法。时频分析是一种处理非平稳信号的有力方法，在对滚动轴承信号处理方面具有广泛应用[3-4]。常见的时频分析有Wigner-Ville分布、短时傅里叶变换(Gabor变换)、希尔伯特黄变换(Hilbert-Huang Transform, HHT)。这些方法都有各自的缺点和不足。如Wigner-Ville分布中具有交叉干扰项存在，短时傅里叶变换窗函数的时频分辨率不能达到最优，HHT在处理复杂信号时体现出了长时间的计算缺点[5]。为了解决传统时频分析法的不足，黄锷等[6]提出了一种较新的时频分析方法，称为经验模态分解(Empirical Mode Decomposition， EMD)方法。但EMD方法存在局限性，算法本身存在模态混叠与端点效应，对噪声敏感以及依赖于插值方法的选择等问题。局部均值分解(Local Mean Decomposition， LMD)方法是由学者Smith[7]提出的一种处理非平稳信号的自适应时频分析方法，LMD在某些方面的性能要优于EMD方法，例如在抑制模态混叠、端点效应、避免过包络、欠包络、迭代次数等方面。LMD方法自适应的将一个复杂的高频信号分解成若干个瞬时频率的具有物理意义的乘积函数PF(Product Function)分量之和。每一个PF分量是由一个纯调频信号和一个包络信号直接求出，其中，包络信号是PF分量的瞬时幅值，而纯调频信号可以求出PF分量的瞬时频率，将全部PF的瞬时频率和瞬时幅值组合便可以得到原始信号完整的时频分布，对此进行更精准有效的处理原始信号特征信息。

文中运用LMD方法对轴承信号进行分解，并从包含有主要故障信息的模态分量中提取特征值作为故障特征向量，然后运用随机森林(RF)对轴承信号进行分类，进而得出此方法的有效性。实验证明，文中提出的LMD与RF相结合的故障诊断方法具有较高的准确率。

1 研究方法

1.1 局部均值分解(LMD)

LMD方法的原理是从原始信号中分离出不同的包络信号和纯调频信号组合，将包络信号和纯调频信号相乘就可以得到一个具有物理意义瞬时频率的PF分量，迭代处理到原始信号的全部PF分量被分离出来，就能得出原始信号的时频分布情况。对于原始信号x(t)，分解过程如下[8]：

1)从原始信号中提取出所有的局部极值点ni，对求出的相邻局部极值点求均值：

(1)

将所有相邻两个平均值点mi用直线连接起来，得到局部均值线段，然后采用滑动平均法进行平滑处理，可得到局部均值函数m11(t)。

2)利用局部均值点，求出两相邻极值点之间的包络估计值

(2)

将全部相邻两个包络估计值ai用直线连接，然后采用滑动平均方法进行平滑处理，得到包络估计函数a11(t)。

3)将局部均值函数m11(t)从原信号x(t)中分离出来，得出

h11(t)=x(t)-m11(t)

(3)

4)用h11(t)除以包络估计函数a11(t)以对h11(t)进行解调，得出

(4)

计算s11(t)的包络估计函数a12(t)，假如a12(t)不等于1，说明s11(t)不是一个纯调频信号，需要重复上述迭代过程，使得s1n(t)成为一个纯调频信号为止，即-1≤S1n(t)≤1，且其包络函数a1(n+1)(t)=1,所以有

(5)

式中

(6)

迭代终止的条件为

(7)

迭代分解过程在实际应用中是无法实现的，为了获得较为理想的纯调频信号，有一个较为合理的迭代终止条件，可以用

a1n(t)≈1

(8)

5)在迭代过程中产生的全部包络估计函数相乘,便可以得到包络信号

(9)

6)将纯调频信号s1n(t)和包络信号a1(t)相乘,便可以得到原信号的PF分量，即

PF1(t)=a1(t)s1n(t)

(10)

7)将第一个分量PF1(t)从原始信号x(t)中分离出来，求解出一个新的信号u1(t),将u1(t)作为原始数据重复以上步骤，循环k次直到uk为一个单调函数为止。

(11)

所有的PF分量和uk重组，可以求出原始信号，即

(12)

说明LMD分解没有造成原信号的丢失。

1.2 特征提取

在LMD分解之后，对各PF分量进行特征值提取，需要提取的特征值有均值、标准差、极差、变异系数、波动指数、能量熵和信息熵。其中，均值、标准差和极差将不详述[9]。

1.2.1 变异系数

对轴承故障信号进行分析时，常用特征有平均值、方差、标准差和变异系数等，其中变异系数可以衡量轴承信号的幅度大小变化,是衡量滚动轴承信号中变异程度的一种统计量。

其定义为：

(13)

其中

式中：l----PF分量的长度。

1.2.2 波动指数

波动指数可以衡量信号变化的强度。滚动轴承故障状态下信号的波动通常会比滚动轴承正常状态下信号的波动剧烈。

定义有：

(14)

式中：l----PF分量的长度。

1.2.3 能量熵

为了便于特征提取，选择能量熵来表征不同类别PF分量特征的差别。根据信息论中能量熵的定义，固有模态函数ci(t)的能量可采用下式计算：

(15)

式中：t1，t2----分别为信号起始时间和信号结束时间。

其定义为：

(16)

式中：Pi----第i个PF分量的能量占整个信号能量的比例，Pi=Ei/E，其中E为整个轴承故障信号的能量。

1.2.4 信息熵

信息中排除了冗余后的平均信息量称为“信息熵”，轴承故障状态下信号的波动通常会比轴承正常状态下信号的信息熵值低。

其定义为：

(17)

式中：x----随机变量。

1.3 识别算法

1.3.1 随机森林

随机森林(Random Forest， RF)是近年来一种比较新的机器学习模型[10]。机器学习模型中比较经典的是神经网络，但神经网络模型计算量非常大。20世纪80年代，Breiman等[10]发明分类树的算法，在2001年,Breiman[11]把分类树组合成随机森林，其实质是采用多棵分类树对样本进行训练并预测的一种新型分类方法。

随机森林{h(x,θk),k=1,2,…}是一个由树形分类器组合而成的集合，集合中的元分类器h(x,θk)是利用CART算法构造的没有剪枝的分类决策树。式中x为输入向量，{θk}为独立同分布的随机向量，由此决定了单棵树的生长过程；森林的输出采用简单多数投票方法，或者是单棵树输出结果的简单平均值得到，具体方法[12]如下：

1)用Bagging方法生成若干个别训练集，即每一个个别训练集都是出自原训练集的n个样品中，并且有放回地抽取其中n个样品；

2)对于每一个个别训练集，用如下方法生成一棵不剪枝的分类回归树；

假设一共有M个原始属性，给出一个正整数mtry，且满足mtry≤M。在每一个内部节点，从M个原始属性中随机抽取mtry个属性作为该分裂节点的候选属性。在整个森林的生成过程中，mtry不变；选出一个最优的分类方式在mtry个候选属性之中对此节点进行分类；令每棵树充分成长，不再进行剪枝；

3)重复上述步骤，直到生成ntree棵分类回归树，并且ntree足够大;

4)进行分类时，如果遇见未知的样本类别，输出的类别名称可以由森林中树的多数投票决定，即：

(18)

随机森林在Bagging的基础上采用了随机选择属性的方法，有效降低了树与树之间存在的相关性，同时建立的单棵不剪枝分类回归树能够得到较低的误差，从而确保了随机森林的分类准确性。

1.3.2 支持向量机

支持向量机(Support Vector Machine， SVM)于1995年正式发表，是数据挖掘中的一项新技术[12]，它是一种有坚实理论基础的新颖小样本学习方法，具有一定的鲁棒性，并且增删非支持向量机样本对模型没有任何影响。

支持向量机是根据给定的训练

T={(x1,y1)，…,(xl,yl)}∈(X×Y)l

(19)

其中，xi∈X=Rn,X为输入空间，输入空间中的每一个xi有n个属性特征组成，yi∈Y={-1,1},i=1,2,…,l。寻找Rn上的实值函数g(x)，以便用分类函数

f(x)=sgn(g(x))

(20)

推导出任意一个模式x对应y的值的问题为分类问题[13]。支持向量机的关键在于核函数选择，文中选择高斯核函数。

2 实证分析

2.1 数据来源

文中数据来源于美国凯斯西储大学(Case Westen Reserve University)轴承资料，数据是基于一个马达电机、一个转矩传感器、一个功率计及电子控制设备的实验平台获取。文中针对轴承在转速为1 797 r/min的情况下进行采集，采样频率为12 kHz，对轴承出现的内圈故障状态、外圈故障状态、滚动体故障状态以及正常状态情况下进行分析，每种状态下采集24个长度为5 000的小样本，采集长度是从初始点到120 000。每个状态下第一次采集的样本原始序列如图1所示。

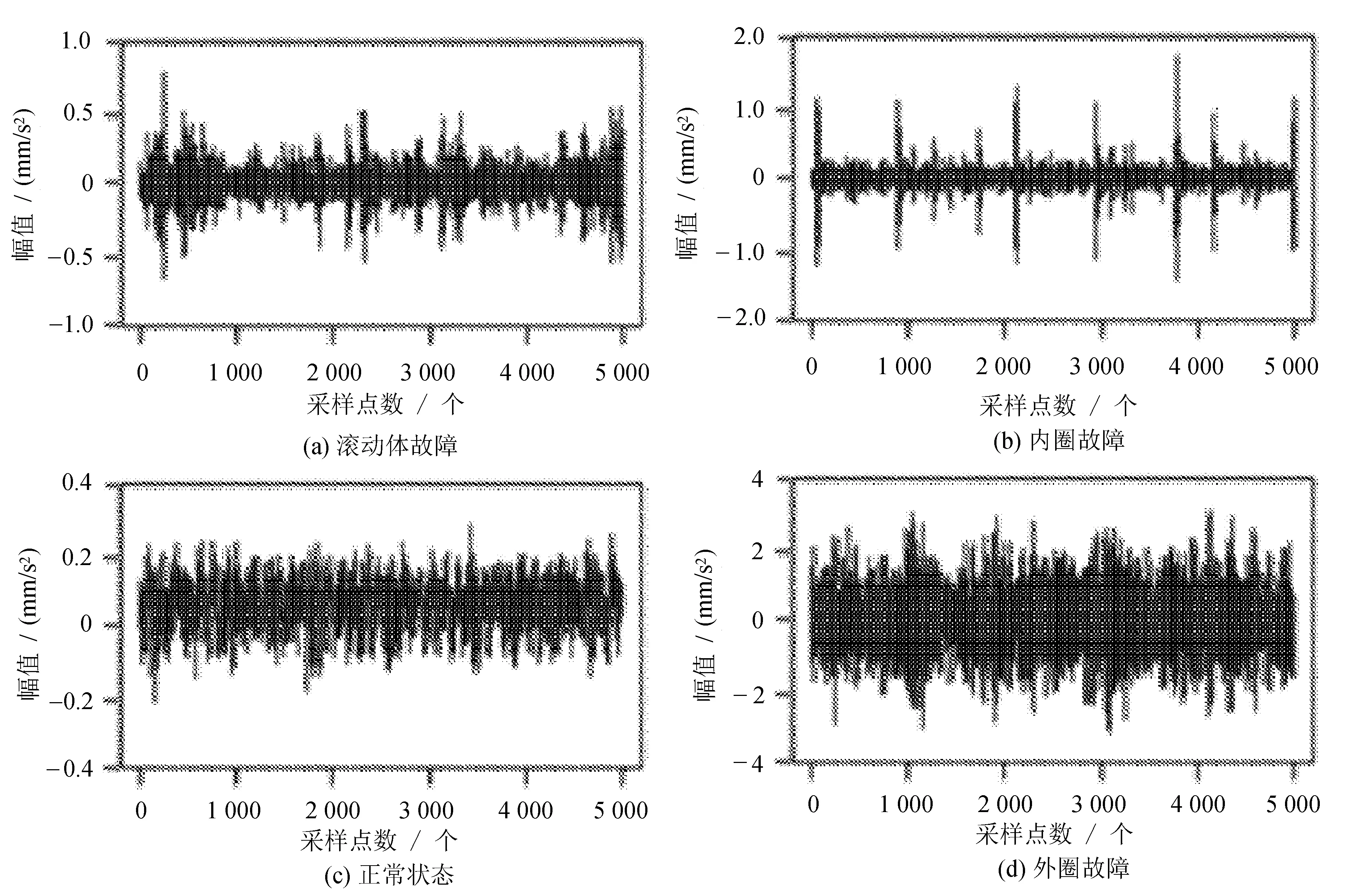
图1 四种状态部分样本集时序图

2.2 LMD分解及特征提取

由于样本数据集较大，文中选择其中一个样本集展示LMD分解过程。选择滚动体故障中的第一个小样本，用LMD对样本序列进行分解。该样本的LMD分解结果如图2所示。

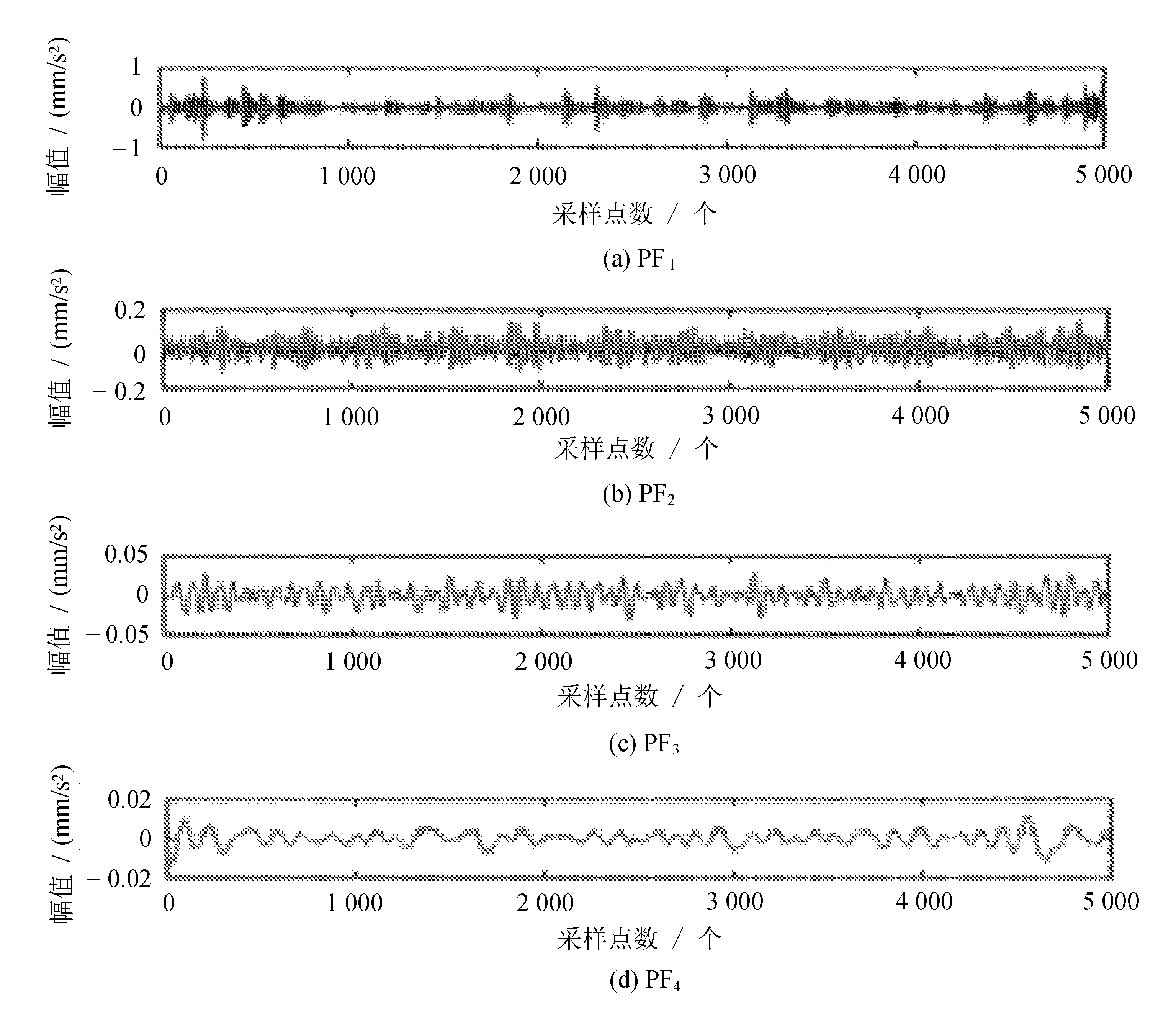
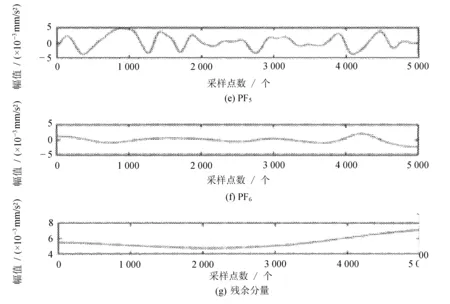
图2 内圈故障样本经LMD分解结果

分解后每一类故障状态都有不同的PF分量。对得到的216个分量按照1.2中的方法计算其对应的均值、标准差、极值、变异系数、波动指数、信息熵和能量熵，得到一个维数为216×7的特征向量。

2.3 故障识别分析

从计算得到的216×7特征向量矩阵中随机抽取156个特征向量作为训练集，剩余的60个特征向量作为测试集。将训练集矩阵输入到RF中，得到一个模型。再将测试集矩阵输入到该模型中进行分类。

RF分类结果见表1。

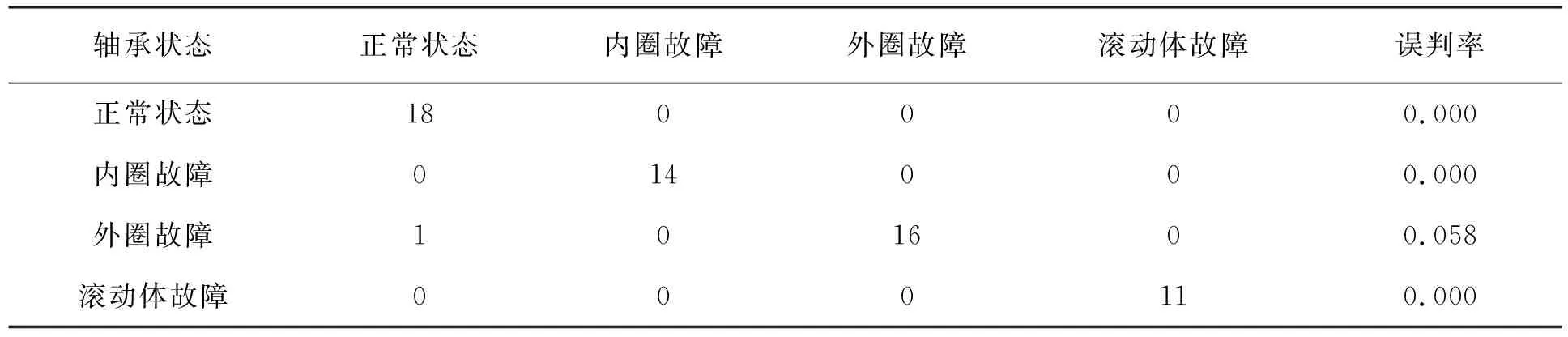
表1 测试集随机森林分类结果

其中行数据为真实故障类型，前四列数据为预测类型，最后一列是误判率，总的误判率为1.67%。重复上述方法，将训练集矩阵输入到SVM中，得到另一分类结果，SVM分类结果见表2(SVM分类的总的误判率为13.33%)。

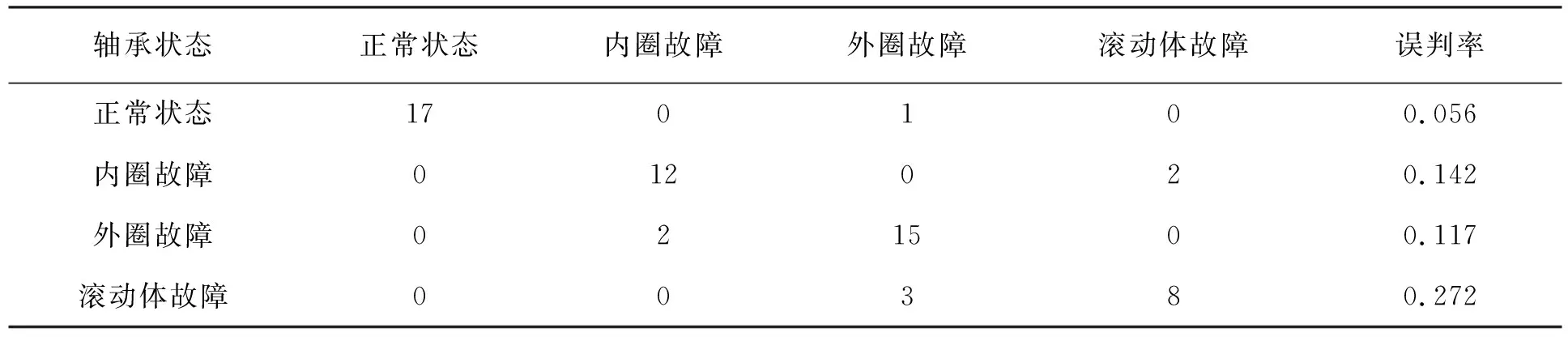
表2 测试集支持向量机分类结果

从表1和表2中可以发现，针对同一组数据集RF和SVM分类故障状态效果相差很大。其中RF分类将1个外圈故障误判为正常状态，而其余状态全部判断正确；SVM分类将1个正常状态误判为外圈故障，2个内圈故障误判为滚动体故障，2个外圈故障误判为内圈故障，3个滚动体故障误判为外圈故障。

对测试样本的错误分类个数和正确率做了总体统计，将表1与表2进行整理得到表3。

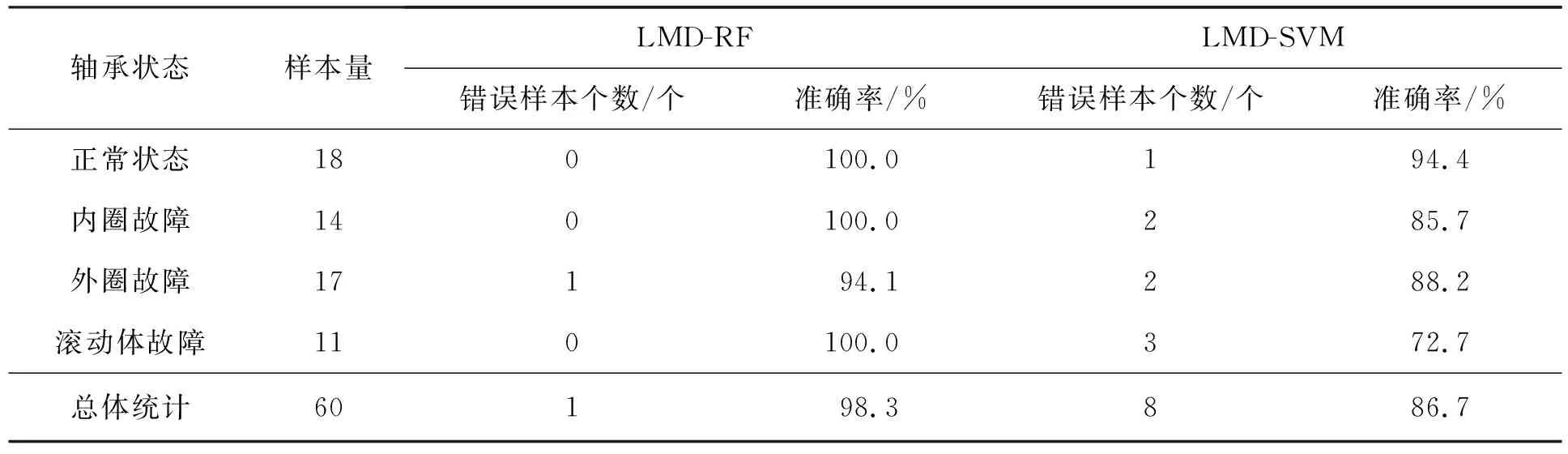
表3 测试集分类结果汇总

从表3可以更清晰地看到,RF分类的准确率在各种状态下都高于SVM分类。

通过以上分析对比，RF分类的精度更高,文中所提出的故障诊断方法能够有效识别出滚动轴承的工作状态和故障类型。

3 结 语

基于滚动轴承的状态监测和故障诊断的现实需要，提出了局部均值分解与随机森林相结合的故障诊断方法。针对实验数据，对滚动轴承信号进行LMD分解，将分解后的PF分量提取均值、标准差、极差等特征值，构造成特征向量，用以随机森林和支持向量机分类。上述实验过程得出结论：文中提出的LMD与随机森林结合的方法具有相对较高的识别精度，可以有效识别出滚动轴承工作状态及故障类型。