非均匀热载荷对统计能量分析参数的影响

陈 强， 杨 轩， 李彦斌， 张 鹏， 吴邵庆， 费庆国

(1. 东南大学 工程力学系，南京 210096; 2.东南大学 空天机械动力学研究所，南京 211189;3.东南大学 机械工程学院，南京 211189)

高超声速飞行器在巡航或再入过程中面临着复杂严酷的高温、振动和噪声环境[1-2]，其中噪声的频率范围可达10～10 000 Hz。随着飞行器结构的轻量化发展，薄壁构件大量应用至结构设计中，这使得结构高频动响应问题越来越受重视。此外，由于飞行速度的不断提升，飞行器服役的环境温度将大幅上升，研究表明高超声速飞行器外表面最高温可达1 000 ℃[3]，热效应成为结构动力学分析中必须考虑的因素。因此，热噪环境下结构高频动响应预示问题越来越受到重视。

对于结构的高频动响应预示，使用低频段常用的有限元法(Finite Element Method，FEM)、边界元法等离散化方法需要划分非常细致的单元，这将导致系统自由度和计算量急剧增加。同时，高频段结构响应对边界条件、材料参数等不确定性因素非常敏感[4]，离散化方法难以给出满足工程需要的结果。因此通常使用平均或统计的振动能量表征结构高频动力学特性。统计能量分析(Statistical Energy Analysis， SEA)[5]是目前结构高频动响应分析中较为常用的方法，该方法将结构划分为若干子系统，通过建立子系统间的能量传递方程，求解子系统的输入功率和振动能量，从而获取系统的平均振动特性。统计能量分析模型的自由度和计算量较小，能够解决高频密集模态问题，且计算结果对系统参数并不十分灵敏，是目前高频激励下结构动力学分析与环境预示的有力工具[6]。

在对结构合理划分子系统的基础上，统计能量分析的精度主要取决于其分析参数的准确性，即系统的模态密度(Modal Density)、单个子系统的内损耗因子(Internal Loss Factor, ILF)、各个子系统间的耦合损耗因子(Coupling Loss Factor, CLF)。目前针对热环境下结构统计能量分析参数的预示已开展了相关研究：Han等[7]基于改进的夹芯板理论，计算了热环境下夹芯板的模态密度和模态数目；张鹏等[8]考虑了温度相关的材料物性参数变化，研究了温度对统计能量分析参数的影响；陈强等[9-10]结合FEM和功率输入法(Power Injection Method，PIM)给出了一种热环境下适用于复杂结构的统计能量分析方法，并研究了不同热效应和结构尺寸参数对统计能量分析参数的影响。以上研究大多针对均匀热载荷作用下的结构开展分析，但由于气动加热及太阳辐射的作用，结构实际面临的热载荷通常是非均匀的[11]。

针对非均匀热载荷作用下的结构动力学分析，国内外已开展了较多相关研究：Mead[12]基于Rayleigh-Ritz理论，研究了非均匀热载荷作用下平板固有频率和模态振型的变化；Du等[13]研究了厚度方向温度梯度对层板板声振响应特性的影响；贺旭东等[14]研究了非均匀温度场作用下结构热应力对机翼结构固有特性的影响；李纪永等[15]研究了薄壁结构在不同周期交变温度及不同稳态温度下的非线性动态响应。目前针对非均匀热载荷对结构动力学特性影响的研究主要集中在固有特性和低频段响应分析方面，涉及高频段统计能量分析的研究较少。由于热效应所引起的材料力学性能参数变化及产生的热应力会使得结构刚度发生变化，热效应对结构动力学特性的影响不能忽视，因此有必要开展热环境下非均匀热载荷对统计能量分析参数的影响研究。

本文基于有限元法和计及热效应的功率输入法，开展非均匀热载荷对结构统计能量分析参数的影响研究。首先介绍热环境下基于功率输入法和功率流模型的结构统计能量分析参数预示方法；随后，通过对比数值解和波方法计算得到的理论解验证分析方法的准确性；最后，研究非均匀热载荷的非均匀程度和平均温度对L型折板结构统计能量分析参数的影响。

1 理论基础

本文结合有限元法和功率输入法(FEM-PIM)预示热环境下结构的统计能量分析参数。具体步骤为：首先通过FEM获取系统考虑热效应的模态、质量矩阵和刚度矩阵；然后使用计及热效应的功率流模型计算结构的输入功率及振动能量；最后结合PIM获取结构的统计能量分析参数。

1.1 计及热效应的功率流模型

非均匀热载荷作用下结构的动力学特性具有非线性特征：一方面，高温使得结构产生热应力，从而产生附加应力刚度矩阵，对结构的刚度产生影响，即具有几何非线性特征；另一方面，高温环境下结构存在非线性的应力-应变关系，即具有材料非线性特征。此外，非均匀热载荷会使得材料物性参数发生变化，导致其刚度改变。本文在计算中主要考虑了几何非线性和材料物性参数变化的影响，建立计及热效应的结构有限元方程为

([Ks+KT+Kσ]+jωC-ω2M)ui=F

(1)

式中：ω为分析频率；Ks为常温下结构的刚度矩阵；KT为材料物性参数变化引起的刚度改变矩阵；Kσ为热应力引起的附加刚度矩阵；C和M分别为结构的阻尼矩阵和质量矩阵；u为节点位移；F为外载荷激励向量。

由计及热效应的有限元动力学方程可知，系统振动的势能V和动能T分别为

(2)

式中：K=Ks+KT+Kσ为总体刚度矩阵。

对于典型L型折板结构，将其划分为a和b两个子系统。其中子系统b的响应向量ub可通过转化矩阵Zb获得，即ub=Zbu。系统b的势能Vb和动能Tb分别为

(3)

式中:Kb和Mb分别为子系统b刚度矩阵和质量矩阵。

通过模态分析可获得系统前n阶模态质量归一化模态振型向量。记第j阶模态的振型向量为φj，前n阶模态振型向量组成的模态振型矩阵为Φ=[φ1,φ2,…,φn]。根据模态的正交性

(4)

式中：ωj为第j模态的固有频率，j∈[1,n]。

第j阶模态受到的模态力Fj及其在该模态力作用下的位移响应Yj为

(5)

当只在子系统a上施加载荷Fu时，在模态坐标系下，系统的振动动能T、势能V和对子系统a的输入功率P分别为

(6)

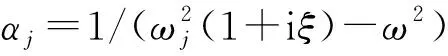
将式(5)代入式(3)中可得，模态坐标系下子系统b计及热效应的动能Tb和势能Vb分别为

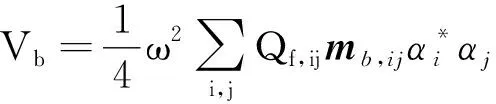
(7)

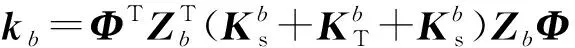
1.2 功率输入法

对于具有两个子系统的结构，其统计能量分析的功率流方程为

(8)

(9)

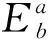
将由式(6)和式(7)计算得到的输入功率、子系统振动能量代入式(8)和式(9)中，联立方程即可求得结构的内损耗因子和耦合损耗因子。

2 数值仿真

为研究非均匀热载荷对结构统计能量分析参数的影响，以夹角为90°的典型L型对称折板为例开展研究，其几何模型如图1所示。将结构划分为板1和板2两个子系统，分别对应子系统a和子系统b，两板尺寸均为L1×L2×t=400 mm×400 mm×1.5 mm。板材料为TA7钛合金，其材料属性如表1所示。由于薄壁结构的振动以弯曲模态为主导，因此采用板单元建立其有限元模型，单元尺寸为5 mm，满足最高分析频率(5 600 Hz)每波长内最少6个单元的尺寸要求。两板除耦合边外各边简支。在计算分析中对各模态施加阻尼比2%的结构阻尼。

图1 L型对称折板Fig.1 L-shaped symmetry folded plate

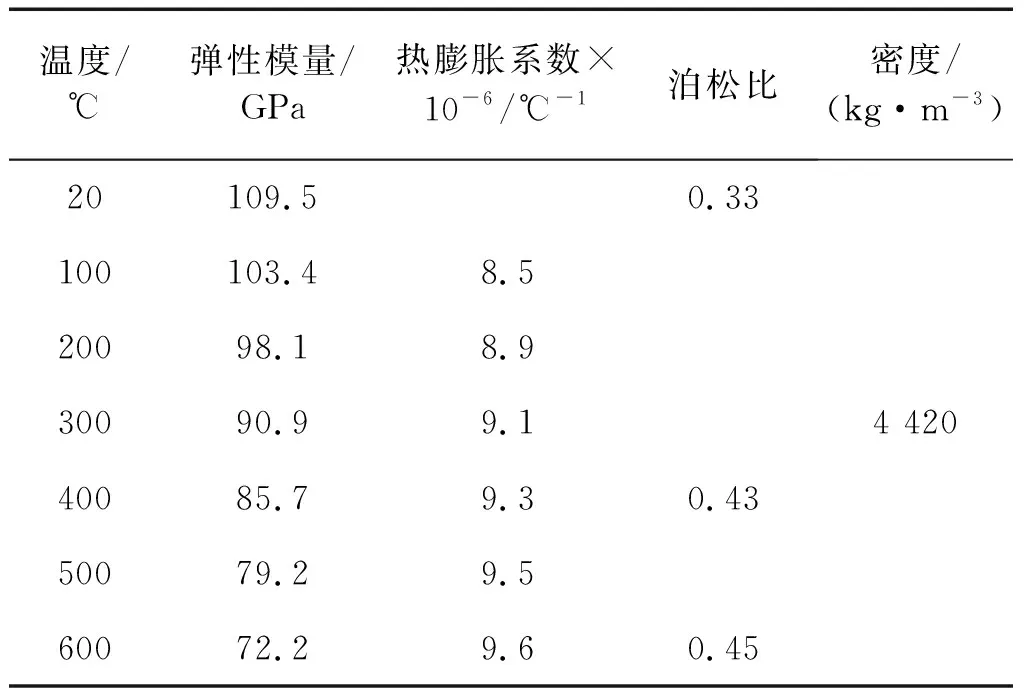
表1 TA7合金材料属性Tab.1 Material properties of TA7

雨流载荷(Rain on the Roof，ROF)[16]是一种空间内各点互不相关的宽带激励，它可以均等地、充分地激励起子系统的局部模态，满足统计能量分析中频带内各模态振动能量相等的假设，对系统各阶模态输入功率相近的载荷。雨流载荷的载荷幅值与作用点的材料密度成正比，对于离散的有限元模型，雨流载荷对应式(15)中Qf里的矩阵A，满足A=S2Ma，其中S表示载荷强度。在后续的算例中均在子系统上施加单位雨流载荷。

计算分析中对板1和板2施加线性变化的非均匀热载荷。为便于后续对比分析，对于非均匀热载荷做出如下定义：热载荷的平均温度为T0；热载荷的最大温差为DT，热载荷的非均匀程度为DT/T0。例如，平均温度为400 ℃、热载荷的最大温差为200 ℃，则热载荷的非均匀程度为0.5，其温度分布如图2所示。此外，在非均匀热载荷对统计能量分析参数的影响研究中，选取2 800～3 550 Hz频段Δω(中心频率为3 150 Hz)为分析频段，并将频段内分析参数进行无量纲化处理，其基准为均匀热载荷下作用下结构的对应参数。

图2 非均匀热载荷分布示意图Fig.2 The distribution of nonuniform temperature

2.1 方法验证

开展温度为20 ℃的均匀热载荷时结构的统计能量分析参数预示分析，采用波方法(Wave Method)验证本文数值方法的准确性。首先对L型折板结构开展模态分析，各频段内结构的模态数目和模态密度如表2所示。由表2可知，当分析频带中心频率低于1 250 Hz时，频带内的模态数小于5。

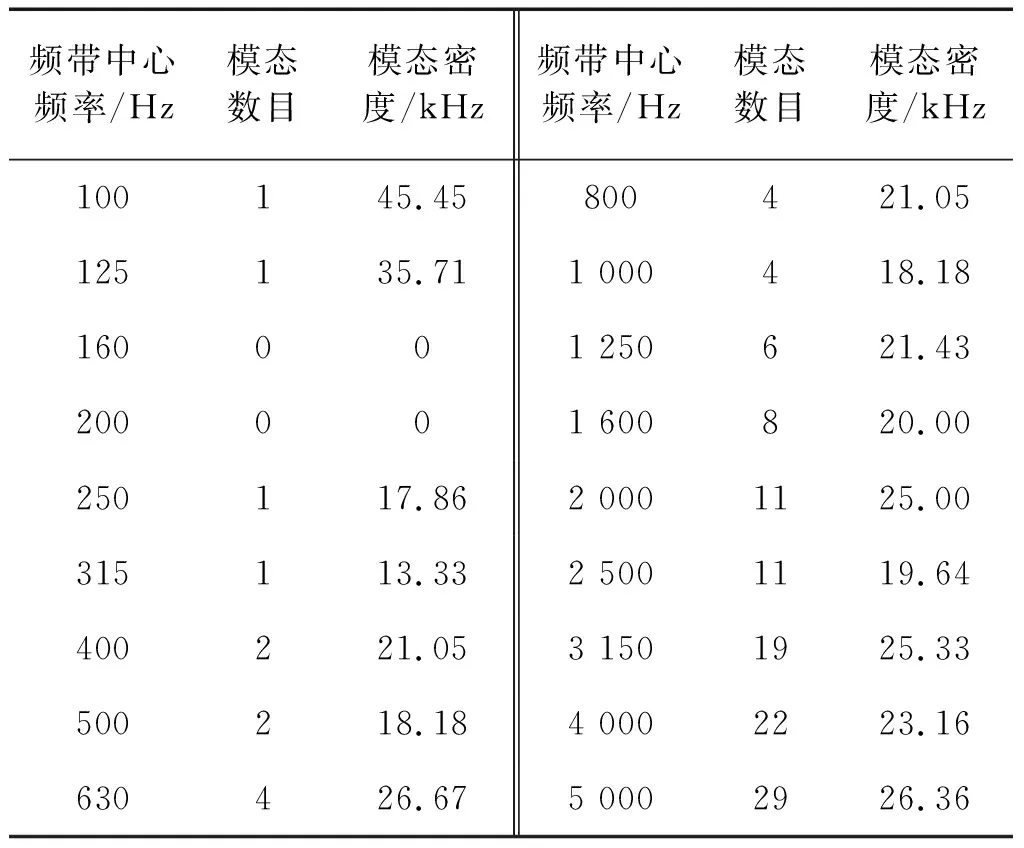
表2 结构各频段内的模态密度和模态数目Tab.2 Modal density and mode counts of structure in different frequency bands

在板1上和板2上依次施加垂直于面板方向的单位雨流载荷，基于FEM-PIM预示结构的统计能量分析参数，由功率注入法计算得到板1的内损耗因子及板1对板2耦合损耗因子的数值解，并将二者与采用文献[17]中波方法计算得到的理论值进行对比分析，计算结果分别如图3和图4所示。由图3和图4可知，当分析频带中心频率低于1 250 Hz时，内损耗因子和耦合损耗因子均与理论解相差较大，这是因为分析频段内模态数较少，未满足统计能量分析中分析频带内模态数大于5的假设条件。随着中心频率的增加，内损耗因子和耦合损耗因子均与理论解基本一致，在1 250～5 000 Hz频段内，内部损耗因子和耦合损耗因子的平均误差分别为6.6%和4.7%。

图3 板1的内损耗因子Fig.3 ILF of plate 1

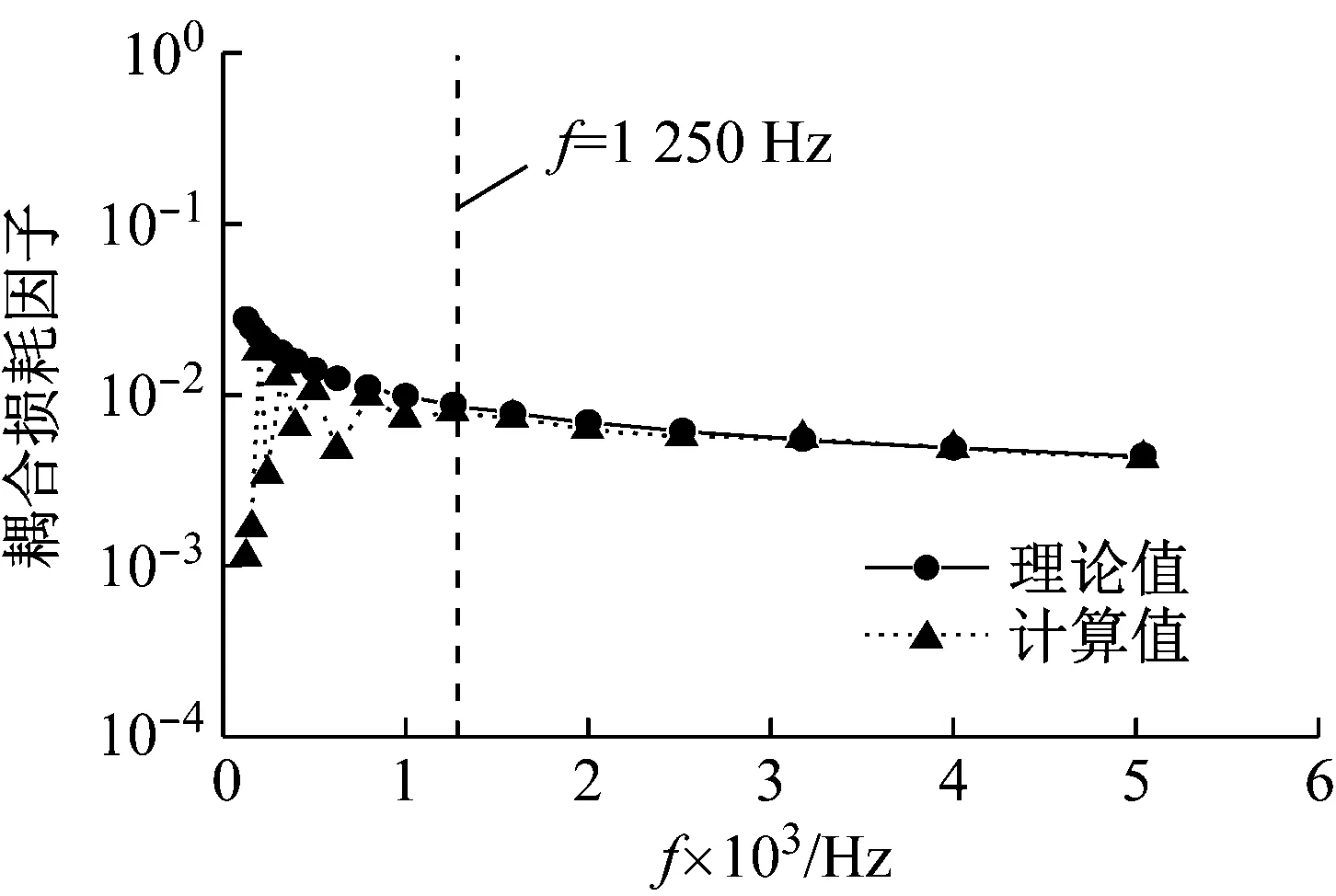
图4 板1对板2的耦合损耗因子Fig.4 CLF of plate 1 to plate 2

由于目前缺乏高温环境下统计能量分析参数的理论解，且高温环境下的高频试验存在高温对实验设备要求较高、测量难度较大及边界条件难以模拟等问题，因此试验开展难度较大。由式(11)和式(12)可知，本文采用的基于FEM-PIM的统计能量分析参数预示方法的准确性主要取决于热环境下系统的固有频率、模态振型、刚度矩阵和质量矩阵等参数的准确性。本文中这些参数主要通过有限元方法获得，目前计及热效应的结构有限元计算精度较高且已有较多研究成果[18-19]，因此本文采用的FEM-PIM方法在高温环境下统计能量分析所得结果也是可信的。

2.2 非均匀程度对统计能量分析参数的影响

为研究非均匀热载荷的非均匀程度对统计能量分析参数的影响，本文选取平均温度为400 ℃、非均匀程度为0.2～1.0的五种热载荷开展研究。首先对结构进行热应力分析，表3给出了不同非均匀程度热载荷下结构的热应力分布和最大幅值。由表3可知，不同非均匀程度热载荷下结构热应力较大的位置均出现在耦合边及约束边界；随着热载荷非均匀程度的增加，结构热应力的最大幅值逐渐增大，且低温边界附近结构的热应力逐渐降低、高温边界附近结构的热应力逐渐上升。

不同非均匀程度热载荷下结构的无量纲化模态密度和输入功率如图5所示，计算结果表明：结构模态密度和输入功率变化趋势基本一致，均随着热载荷非均匀程度的增加而逐渐降低，这主要由于雨流载荷假设为各模态的输入功率基本一致，因此相同频段内，模态密度的下降会使得输入功率降低。相比于均匀分布热载荷作用下的结构，平均温度为400 ℃、非均匀程度为1.0的热载荷作用下结构的模态密度和输入功率分别降低了4.7%和10.8%。

表3 结构热应力Tab.3 Thermal stress of structure

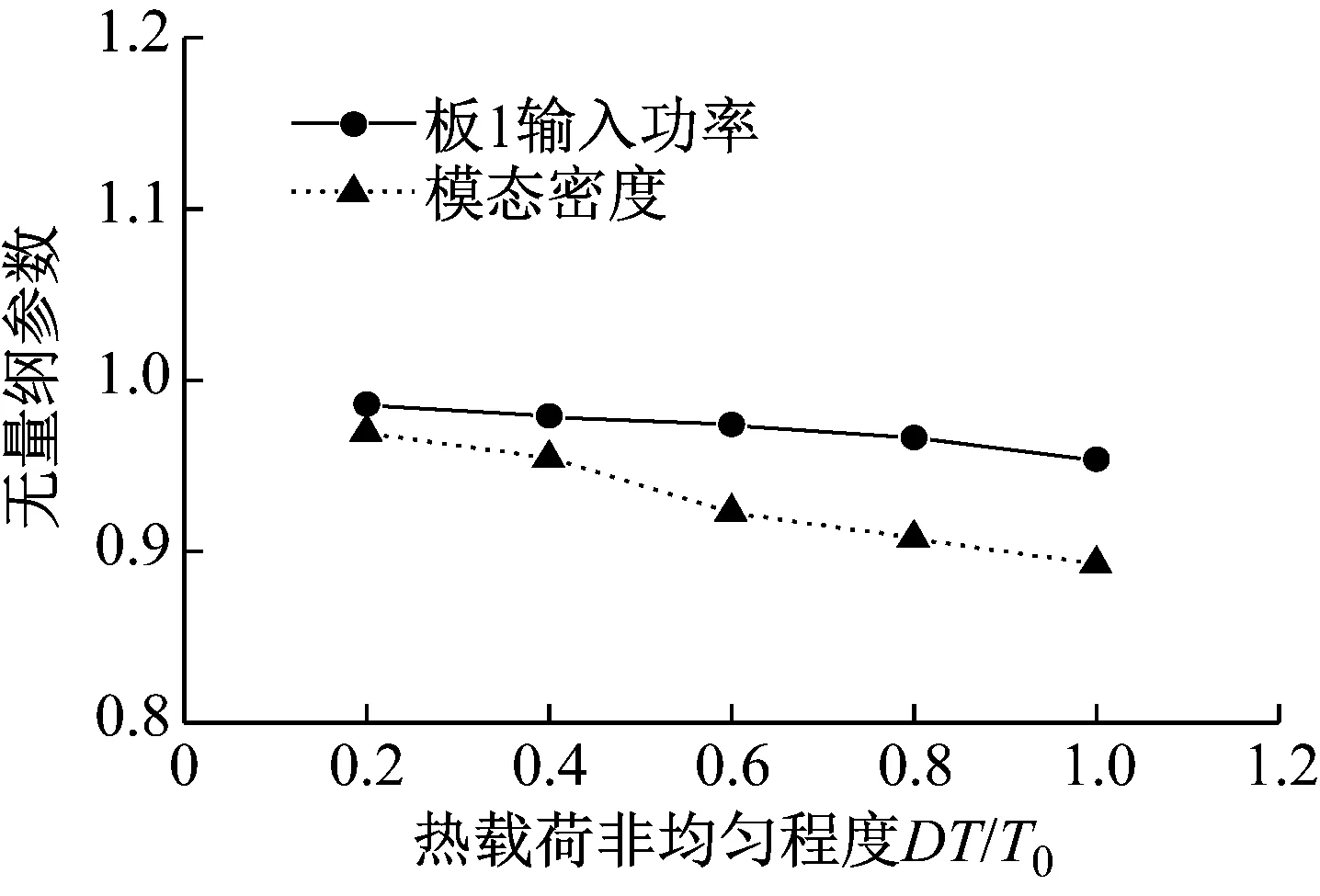
图5 不同非均匀热载荷下无量纲化模态密度及输入功率Fig.5 Dimensionless modal density and injected power under thermal loads with different temperature gradients

不同非均匀程度热载荷下板1和板2的无量纲化振动能量如图6所示。计算结果表明：随着热载荷非均匀程度的增加，板1的振动能量逐渐升高、板2的振动能量逐渐降低；相比于均匀分布热载荷作用下的结构，平均温度为400 ℃、非均匀程度为1的热载荷作用下板1的振动能量升高了4.6%、板2的振动能量降低了7.1%；这主要这是由于高温使得结构发生了热变形，热变形在约束条件下使结构内部产生预拉或预压应力或二者同时存在，使得结构发生软化或硬化；热应力对结构的质量分布影响较小，但其产生的附加刚度改变了结构的整体刚度分布，从而使得结构振型和固有频率发生变化，进而影响结构的振动能量。

图6 不同非均匀程度热载荷下板1和板2的无量纲化振动能量Fig.6 Dimensionless vibration energy of plate 1 and plate 2 under thermal loads with different temperature gradients

不同非均匀程度热载荷下板1的无量纲化内损耗因子和板1对板2的无量纲化耦合损耗因子如图7所示。计算结果表明：随着热载荷非均匀程度的增加，板1的内损耗因子和板1对板2的耦合损耗因子逐渐降低；相比于均匀分布热载荷作用下的结构，平均温度为400 ℃、非均匀程度为1的热载荷作用下结构的模态密度和输入功率分别降低了5.6%和21.7%；这主要是由热载荷的非均匀程度对子系统振动能量的影响所导致的。

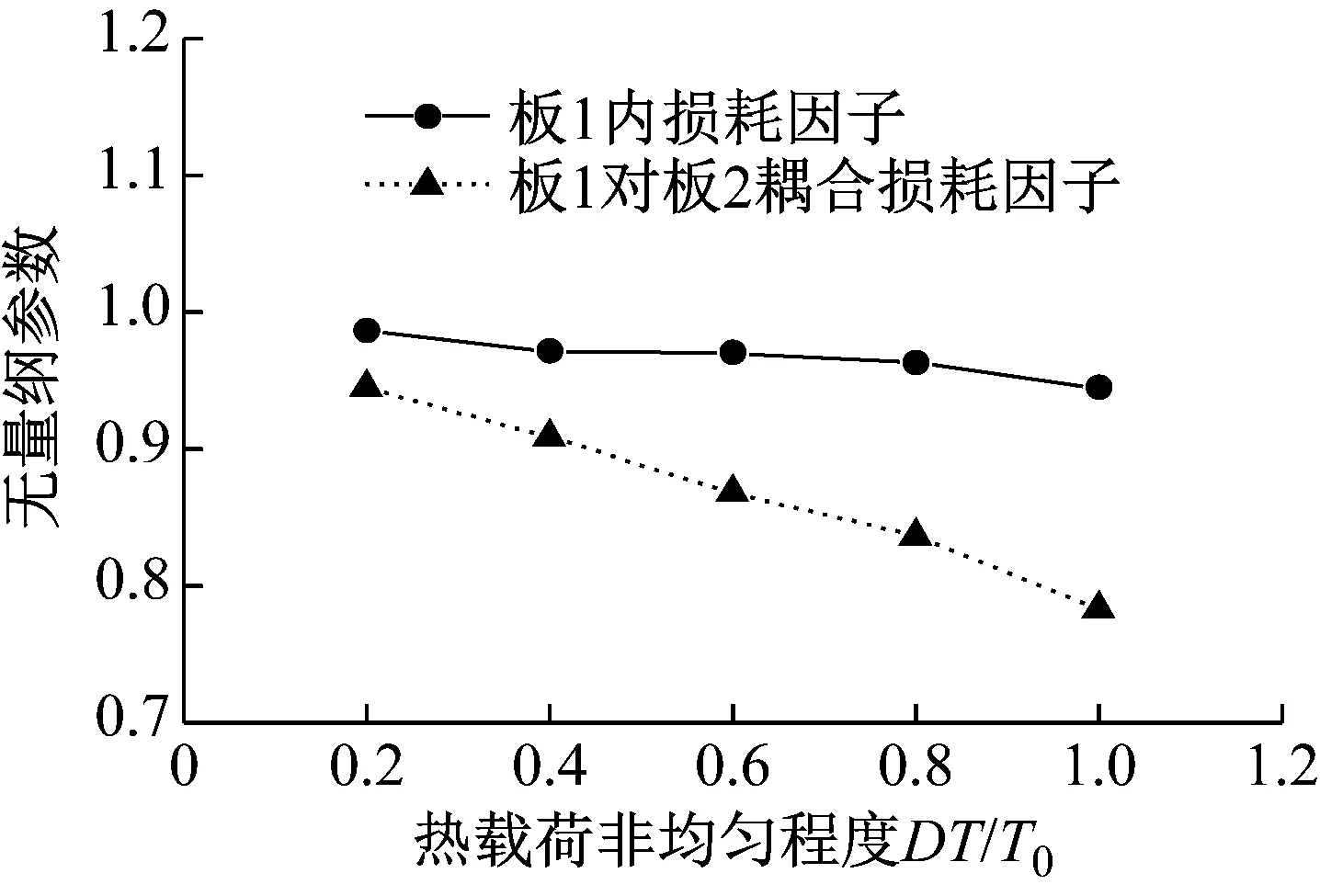
图7 不同非均匀程度热载荷下板1的无量纲化内损耗因子和板1对板2的无量纲化耦合损耗因子Fig.7 Dimensionless IFL of plate 1 and CLF of plate 1 to plate 2 under thermal loads with different temperature gradients

2.3 平均温度对统计能量分析参数的影响

为研究热载荷的平均温度对统计能量分析参数的影响，本文选取非均匀程度为0.5、平均温度为200～400 ℃的五种热载荷开展研究，同时以200～400 ℃均匀热载荷作用下的结构为基准进行对比分析。首先对结构进行热应力分析，计算得到如表4所示的不同热载荷下结构的热应力分布和最大幅值。由表4可知，随着热载荷平均温度的增加，结构热应力的最大幅值逐渐升高，结构边界附近热应力分布的变化较大。

2.4 平均温度对统计能量分析参数的影响

不同平均温度热载荷下结构的无量纲化模态密度和输入功率如图8所示。计算结果表明：随着热载荷平均温度的增加，热载荷的非均匀分布对结构模态密度和输入功率影响逐渐增大，这主要是由于平均温度的升高大大增加了结构的热应力并改变了结构的弹性模量，进而改变了结构的固有频率，使得结构的模态密度和输入功率发生变化。

表4 结构热应力Tab.4 Thermal stress of structure

图8 不同平均温度热载荷下无量纲化模态密度及输入功率Fig.8 Dimensionless modal density and injected power under thermal loads with different average temperatures

不同平均温度热载荷下板1和板2的无量纲化振动能量如图9所示。由图9可知：随着热载荷平均温度的增加，热载荷的非均匀分布对板1和板2的振动能量的影响逐渐增大；这主要是由于热载荷平均温度较高时，热载荷的非均匀分布对结构热应力的分布影响相对较大，进而对结构的振动能量产生较大影响。不同热载荷下板1的无量纲化内损耗因子和板1对板2的无量纲化耦合损耗因子如图10所示。由图10可知：随着热载荷平均温度的增加，热载荷的非均匀分布对板1的内损耗因子和板1对板2的耦合损耗因子的影响逐渐增大，这主要是由非均匀热载荷的平均温度对子系统振动能量的影响所导致的。

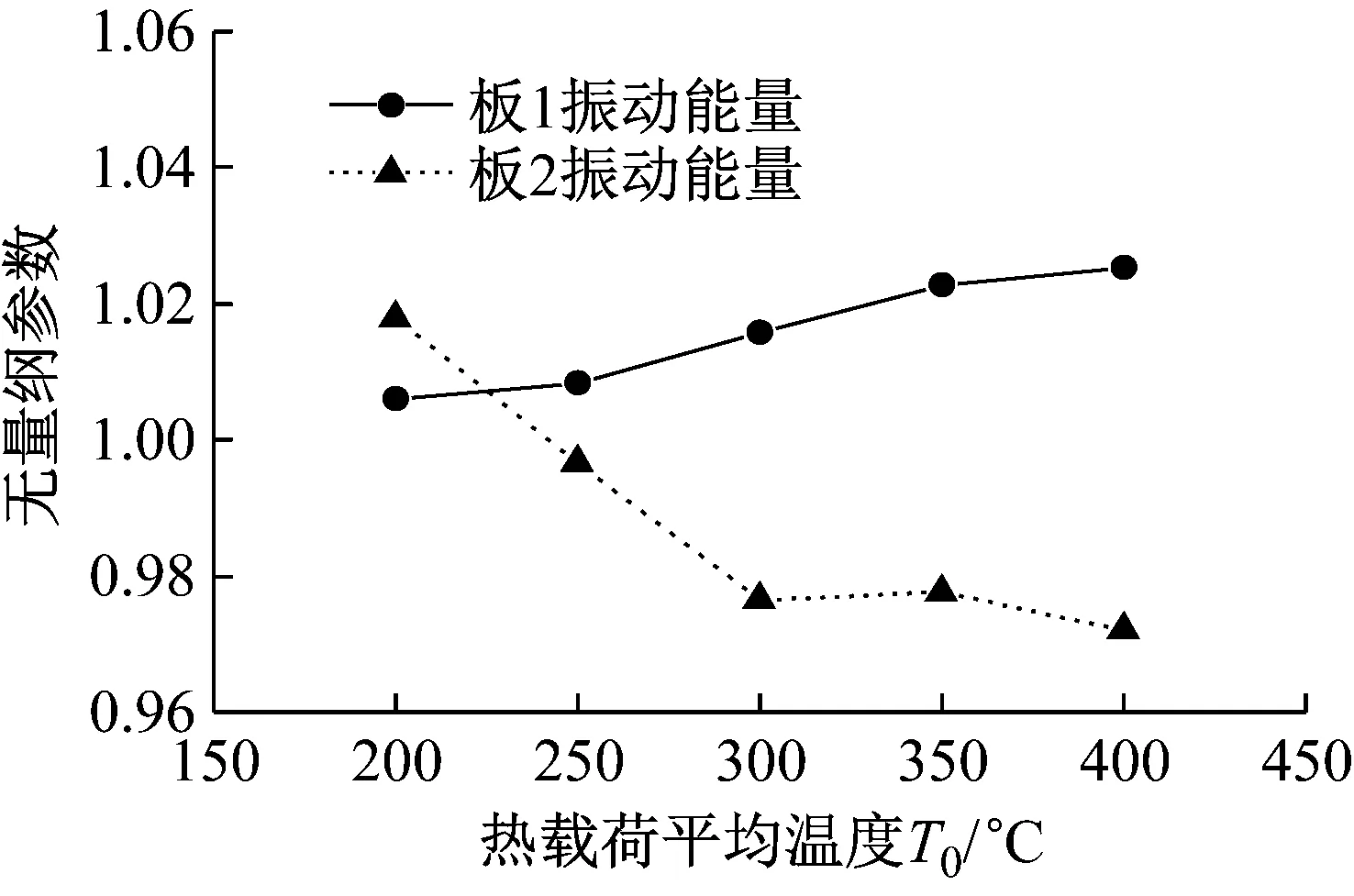
图9 不同平均温度热载荷下板1和板2的无量纲化振动能量Fig.9 Dimensionless vibration energy of plate 1 and plate 2 under thermal loads with different average temperatures

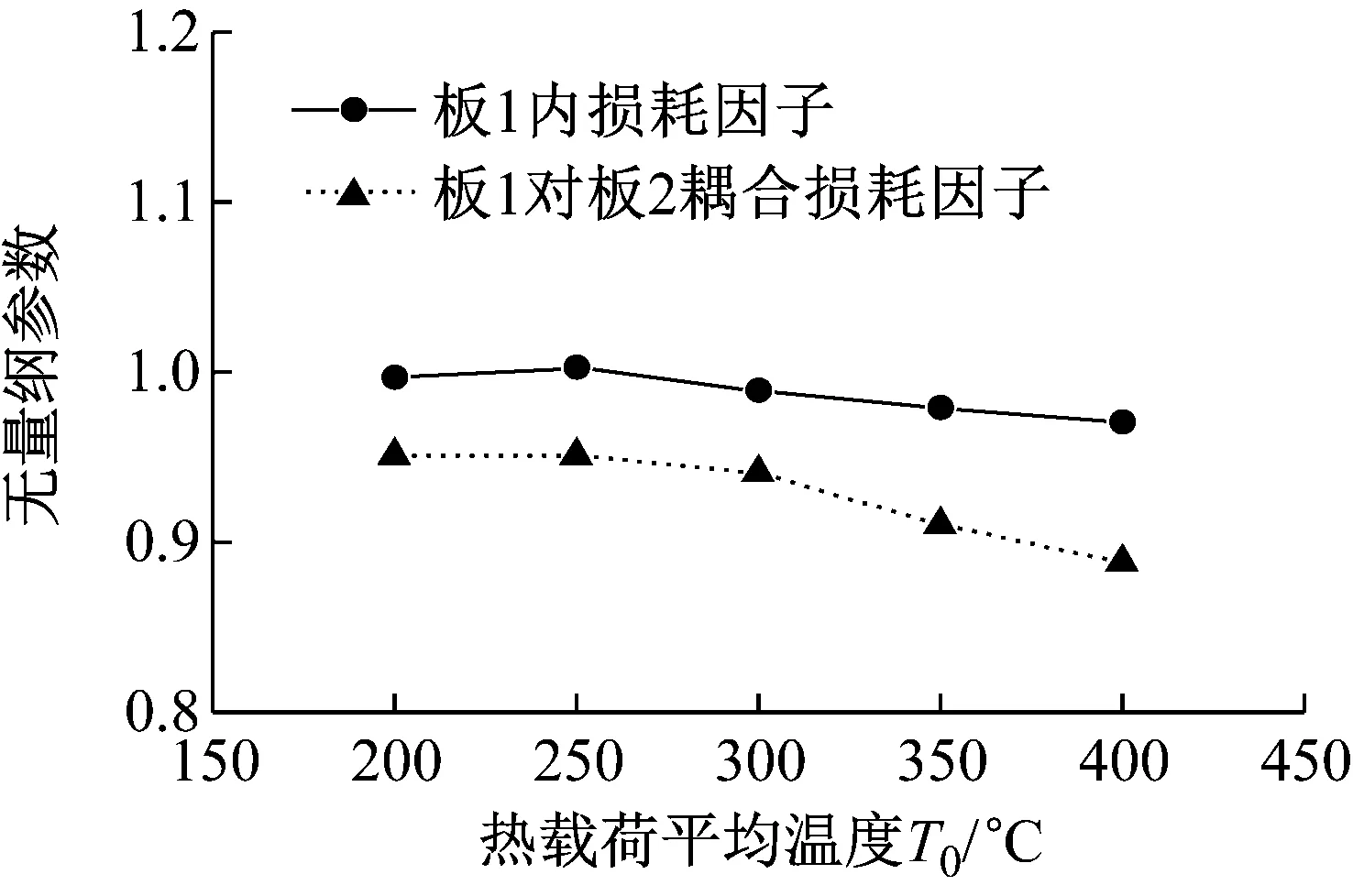
图10 不同平均温度热载荷下板1的无量纲化内损耗因子和板1对板2的无量纲化耦合损耗因子Fig.10 Dimensionless IFL of plate 1 and CLF of plate 1 to plate 2 under thermal loads with different average temperatures

3 结 论

本文基于有限元法和模态坐标系下计及热效应的功率输入法，开展了非均匀热载荷对统计能量分析参数的影响研究。首先对比了单位雨流载荷作用下，子系统内损耗因子及子系统间耦合损耗因子的数值解与解析解，验证了数值方法的正确性。随后研究了非均匀热载荷的平均温度和非均匀程度对L型折板结构统计能量分析参数的影响。结果表明：

(1) 对于不同非均匀程度、相同平均温度热载荷作用下的L型折板结构，热载荷非均匀程度的增加使得其模态密度下降，同时导致结构的内损耗因子和耦合损耗因子的下降，非均匀程度对结构耦合损耗因子的影响较大。

(2) 热载荷平均温度的增加使得热载荷的非均匀分布对L型折板结构统计能量分析参数的影响逐渐增大。