时间尺度上相空间中力学系统的Mei对称性及守恒量

孙 晨，朱建青

（苏州科技大学 数理学院，江苏 苏州215009）

时间尺度理论[1]是Hilger于1988年提出的，它的主要思想在于把连续和离散统一起来分析，已在工程、经济等领域得到应用[2-4]。在2004年Martin Bohner[5]研究时间尺度上的变分原理后，这一理论迅速发展。随后，Torres[6-7]等人将时间尺度与动力学系统相结合，给出了时间尺度上完整系统的Noether定理。在此基础上，蔡平平[8]、张毅[9]、祖启航[10]、施玉飞[11]等人分别研究了时间尺度上非保守非完整系统的Noether理论、Hamilton系统中的Noether理论、非完整力学系统的Noether对称性和守恒量以及Birkhoff系统中的Noether理论。自此关于时间尺度上动力学系统的对称性和守恒量的研究开始起步。Mei对称性是梅凤翔[12]教授于2000年提出的一种不同于Noether对称性和Lie对称性的新型对称性，随后方建会[13-14]研究了相空间力学系统的Mei对称性、Lie-Mei对称性，张毅[15-17]研究了相空间中约束力学系统的对称性。目前关于Mei对称性的研究已取得一些成果[18-25]。笔者应用时间尺度理论研究时间尺度上相空间中的Mei对称性及守恒量，给出了该系统的Mei对称性的定义，得到了其确定方程和守恒量，并举例说明结果的应用。

1 时间尺度上相空间中力学系统的运动微分方程

设力学系统的位形由n个广义坐标qs（s=1，2，…，n）来确定，时间尺度上一般完整系统在广义坐标下的方程可写为[7]

其中 L=L（t，qsσ，qsΔ）为 Lagrange 函数，Qs=Qs（t，qsσ，qsΔ）为非势广义力。

时间尺度上广义动量和Hamilton函数为

对（3）式进行变分运算并考虑（2）式，有

另一方面

对（5）式进行变分运算，有

比较（4）式和（6）式，并考虑（1）式有

因此，时间尺度上相空间中力学系统的运动方程为

2 时间尺度上相空间中力学系统的Mei对称性及确定方程

首先，引进无限小变换[9]

在无限小变换（9）下，H=H（t，qsσ，ps）和 Qs=Qs（t，qsσ，ps）变成 H*=H（t*，（qs*）σ，ps*）和 Qs*=Qs（t*，（qs*）σ，ps*）。

定义1在无限小变换（9）下，如果变换后的函数H*，Qs*仍满足原方程，即

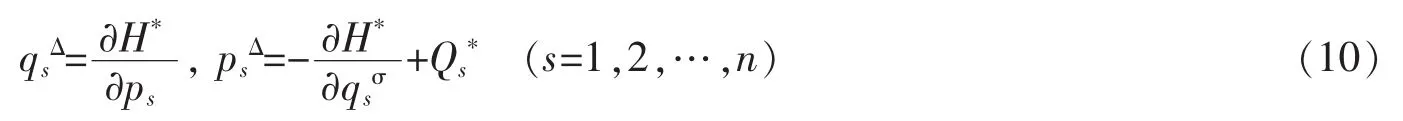
则称这种不变性为系统的Mei对称性。

定理 1对于系统（8），若无限小变换的生成元 ξ0，ξs，ηs满足

则系统（8）具有Mei对称性，其中

方程（11）称为时间尺度上相空间中力学系统（8）的Mei对称性的确定方程。

证明展开 H*和 Qs*，有

将（13）式代入方程（10）有

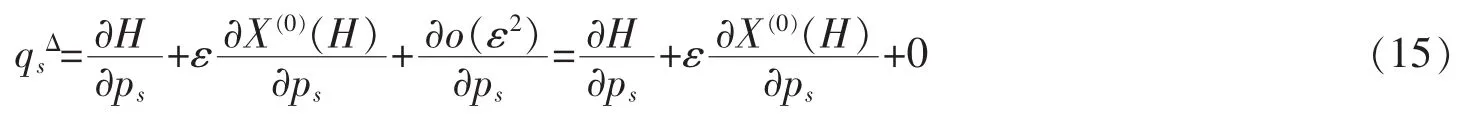
利用（8）式可得到

将（13）、（14）式代入方程（10）有

利用（8）式可得到

于是得到定理1。证毕。

3 时间尺度上相空间中力学系统的Mei对称性导致的守恒量

定理 2在无限小变换（9）下，如果系统（8）具有 Mei对称性且存在规范函数 GN=GN（t，qσ，p）满足条件

则系统有守恒量

证毕。

推论 1如果时间尺度 T=R，则 σ（t）=t，μ（t）=0 于是可由（19）式得出经典结构方程

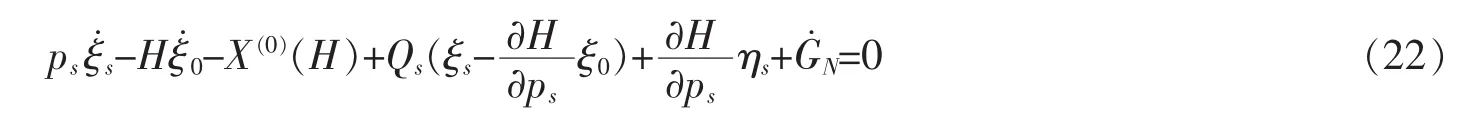
则得到经典的相空间中力学系统的守恒量[13]

4 算例

例1设时间尺度为

系统的Lagrange函数为

试研究系统的Mei对称性。

系统的广义动量和Hamilton函数为

由时间尺度（24）可得时间尺度的前跳算子σ（t）以及步差函数μ（t）

由（8）式可得

通过确定方程（11）给出

方程（31）有解

将（32）式代入结构方程（19）中得

由（20）式可得系统的守恒量

例2设时间尺度为

系统的Lagrange函数为

试研究系统Mei对称性。

系统广义动量和Hamilton函数为

由时间尺度（36）得时间尺度的前跳算子σ（t）以及步差函数μ（t）

由（8）式可得

通过确定方程（11）给出

方程（43）有解

将（44）式代入结构方程（19）中得

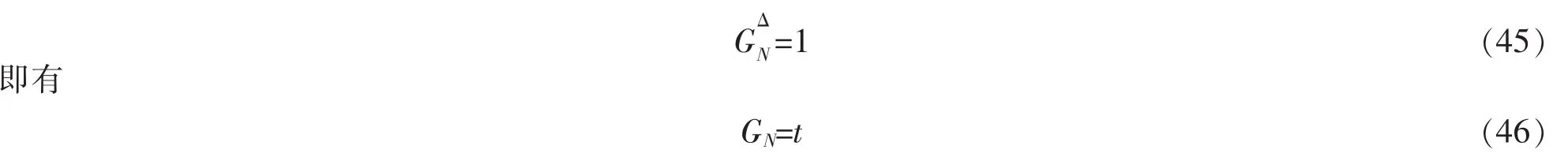
由（20）式可得系统守恒量

5 结语

笔者研究了时间尺度上相空间中力学系统的Mei对称性与守恒量问题。主要工作有：建立了时间尺度上相空间中的运动微分方程；给出了系统下Mei对称性的定义和判据，得到了该系统Mei对称性导致的守恒量；并指出了当时间尺度T=R时Mei对称性导致的经典守恒量的表达形式。这种统一讨论连续与离散系统Mei对称性及守恒量的方法，也可望适用于Birkhoff系统、非完整约束力学系统等约束力学系统的讨论。