Noether symmetrical perturbation and adiabatic invariants for systems of generalized classical mechanics based on El-Nabulsi's fractional model
DING Jinfeng,ZHANG Yi
(1.School of Mathematics and Physics,SUST,Suzhou 215009,China;2.School of Tianping,SUST,Suzhou 215011,China;3.School of Civil Engineering,SUST,Suzhou 215011,China)
Abstract: Under the framework of El-Nabulsi's fractional model,we studied the exact invariants and adiabatic invariants for generalized classical mechanics system with high-order Euler-Lagrange equations.Firstly,based on the invariance of generalized El-Nabulsi-Hamilton action under the infinitesimal transformation,we established the Noether theorems for generalized classical mechanics system with no disturbance and explored the relationship between the Noether symmetries and the exact invariants.Secondly,we investigated the perturbation to Noether symmetries for the system under the action of small disturbance and obtained the adiabatic invariants caused by the perturbation to Noether symmetries.Finally,an example was given to illustrate the application of the results.
Key words: Noether symmetrical perturbation;adiabatic invariant;exact invariant;generalized classical mechanics system;El-Nabulsi’s fractional model
1 Introduction
As well known,most methods of classical mechanics like Lagrangian mechanics and Hamiltonian mechanics are just suitable for conservative systems,while the physical phenomena and the dynamic systems which can be observed in reality are almost nonconservative.So it is significant to model the nonconservative systems.In 1996,Riewe[1-2]introduced fractional calculus to nonconservative systems for the first time in order to study the dynamical modeling problems for a nonconservative system,the fractional Euler-Lagrange equations and fractional Hamilton equations are derived.The modeling approaches of nonconservative dynamics based on the fractional calculus are valued by scientists and are developed constantly ever since,and have aroused highly concern by many scholars,such as, Klimek, Agrawal,Baleanu,Atanackovi[3-6], et al.In 2005,under the framework of fractional calculus El-Nabulsi put forward a new method aimed at nonconservative dynamical models[7],which can be called El-Nabulsi’s fractional model (ENFM).In this model,the form of the resulting equations is similar to the classical Euler-Lagrange equations.The new equations with no fractional derivative but contain a dissipative force that depends on time.Using this new model,one not only avoids the complicated fractional calculus but also gets the nonconservative dynamical models handled.In recent years,ENFM has been further generalized to Lagrangian systems contain high-order derivatives[8],to the systems with holonomic constrains or nonholonomic constrains or dissipative dynamic systems[9].Under the frame of ENFM,El-Nabulsi and Torres considered the fractional variation problems[10],Zhang and coauthors studied the Noether symmetries and conserved quantities[11-12].El-Nabulsi applied the fractional action-like variational approaches (FALVA)to discuss the variation of fractional graviton masses under certain restriction on the range of specific parameters[13],and also applied FALVA to Schrödinger equations in quantum mechanics as well[14].It follows that ENFM is a useful technique,and it is used to describe nonconservative dynamics systems as well as quantum mechanics,optics and other different fields of science.
The symmetry is also called invariance,playing an important role in mathematics,physics and other fields.In 1918,German mathematician Noether first studied the invariant properties of Hamilton action under the infinitesimal transformations related to generalized coordinates and time[15].Since then,Noether theorems have gained high attention by physicists and dynamicists[16-19].Based on ENFM Frederico and Torres studied the invariance in fractional variational problems firstly,and obtained the Noether theorems in the Riemann-Liouville fractional derivative[20-21],Zhang and coauthors studied Noether theorems for Birkhoffian systems[22]and nonholonomicsystems[23].Chen and Zhang established the perturbation to Noether symmetries and adiabatic invariants for Hamiltonian systems[24].
The Lagrange equations of dynamics systems containing high-order derivatives of generalized coordinates with respect to time are called generalized classical mechanics system or high-order derivative systems for short.In 1848,Ostrogradsky and Jacobi studied high-order derivative systems (HODS) firstly.From then on,many important results have been acquired[25-29].The research of high-order derivative systems especially the singular systems with high-order derivative is important to the gravitation theory,gauge theory,relative dynamics of particle,supersymmetry and string theory and other numerous fields of science.
In 1917,Bugers proposed the concept of adiabatic invariant for the first time aimed at a special kind of Hamiltonian system.Since then,lots of significant research achievements are obtained by Djukic,Beulanov,Shasharina,Notte,et al[30-32].The adiabatic invariant is also called gradual invariant,and can be understood as the invariable quantity when some parameters of the system vary slowly.Actually,the slow-varying of parameters is equal to the action of small disturbance.The variation of symmetry under the action of small disturbance and its invariable quantity are closely related to the integrability of the system.There are many applications of the adiabatic invariant theory.For instance,it’s an important way of holding time of simple pendulum with variable length,and nowadays the similar theories are applied to quartz crystal unit of modern horologe.In 1996,Zhao and Mei gave the exact invariant and the adiabatic invariant of a general dynamical system[33].Chen and Zhang obtained the exact invariant and the adiabatic invariant for nonholonomic systems of non-Chetaev’s type based on ENFM[34].Song and Zhang studied perturbation to Noether symmetries for generalized Birkhoff systems based on ENFM[35].
In this paper,the exact invariants and the adiabatic invariants for generalized classical mechanics system based on ENFM are studied.The variation of generalized Hamilton action based on the new model is presented for the first time.The Noether theorems and the exact invariants caused directly by Noether symmetries of the system we discussed are derived,as well as the problem of perturbation to Noether symmetries and adiabatic invariants for the system disturbed by a small force of perturbationl.
2 Perturbation and adiabatic invariants for systems based on ENFM
In this section,three main results will be given.Firstly,the equations for this system are obtained.Secondly,Noether symmetries and exact invariants based on ENFM are introduced.Finally,perturbation to Noether symmetries and adiabatic invariants for the system are presented.
2.1 Generalized Lagrange equations based on ENFM
Under the frame of ENFM,one supposes that the configuration of the system is determined by n generalized coordinates qs(s=1,2,…,n),and the Lagrangian is L(τ,q,q˙,q¨,…,q(m))which is a function of time τ,generalized coordinates qs,and derivatives of qswith respect to t from first order to mth order.
The condition that the generalized El-Nabulsi-Hamilton action

has its extremum values is that the generalized Euler-Lagrange equations based on ENFM hold[8].

When α=1 the equation (2) turns to be generalized Lagrange equations for HODS[25]

2.2 Noether symmetries and conserved quantities
Introduce the infinitesimal transformations of r-parameter finite group of transformation
and their expansion formulae

where εσ(σ=0,1,…,r) is infinitesimal parameters,and ξ0σand ξsσare generators of the infinitesimal transformations.Under the infinitesimal transformation(4),the trajectory γ is transformed to the nearby one,and the generalized El-Nabulsi-Hamilton action becomes

The variation ΔS is the main linear part to ε in the difference S()-S(γ).According to the relationship between the non-isochronous variation and the isochronous variation,that is


Making use of(7),where S is an arbitrary differentiable function,we obtain that
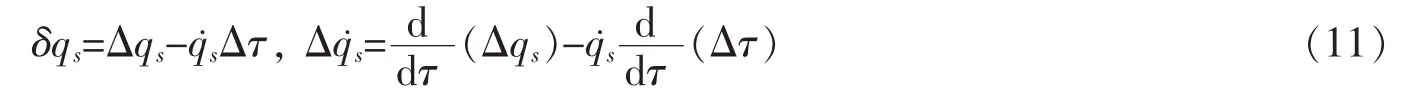
Having in mind (11),form (8) and (9),formula (10) is equivalent to

From (5) it follows that(11) can be expressed as

and then the formula (14) is equivalent to

The formulae (10) and (16)are basic formulae of the variation of generalized El-Nabulsi-Hamilton action.
Definition 1If each of the transformations(4) always holds

the transformations are called symmetrical transformations in Noether's sense of HODS based on ENFM.
According to Definition 1 and formulae (10) and (16),we can obtain the following criteria.
Criterion 1For the infinitesimal transformations of group (4),if the condition
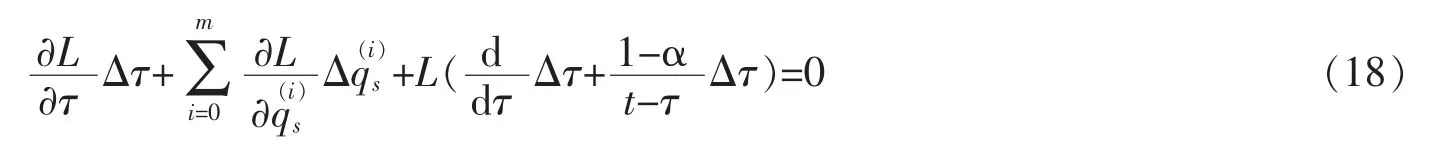
is satisfied,then the infinitesimal transformations are called Noether symmetrical transformations of HODS based on ENFM under the Definition 1.
Condition (18) can also be expressed as

when r=1,formula (19) can be called Noether identity of HODS based on ENFM.
Criterion 2For the infinitesimal transformations of group (5),if the condition


is satisfied,then the infinitesimal transformations are Noether symmetrical transformations of the systems under Definition 1.
We can verify Noether symmetries of the systems we discussed by using Criterion 1 and Criterion 2.
Definition 2If each of the transformations(4) always holds

where ΔG=εσGσwith Gσ=Gσ(τ,q,q˙,q¨,…,q(m)),the transformations are called quasi-symmetrical transformations in Noether's sense of HODS based on ENFM.
According to Definition 2 and formulae (10) and (16),we can obtain the following criteria.
Criterion 3For the infinitesimal transformations of group (4),if the condition

is satisfied,then the infinitesimal transformations are called Noether quasi-symmetrical transformations of HODS based on ENFM under Definition 2.
Condition (22) can also be expressed as

when r=1,formula (23) can be called Noether identity of HODS based on ENFM.
Criterion 4For the infinitesimal transformations of group (5),if the condition

is satisfied,then the infinitesimal transformations are Noether quasi-symmetrical transformations of the systems under Definition 2.
We can verify Noether quasi-symmetries of the systems we discussed by using Criterion 3 and Criterion 4.
If there exist Noether symmetries of HODS based on ENFM,the corresponding conserved quantities will be found.Then,we have the following theorems.
Theorem 1For the systems (2) we discussed,if the infinitesimal transformations of group (4) are the Noether symmetric transformations under Definition 1,then the systems exist r linear independent conserved quantities,which are

ProofAccording to Definition 1,we have

substituting formula (16) into the above equation,we obtain
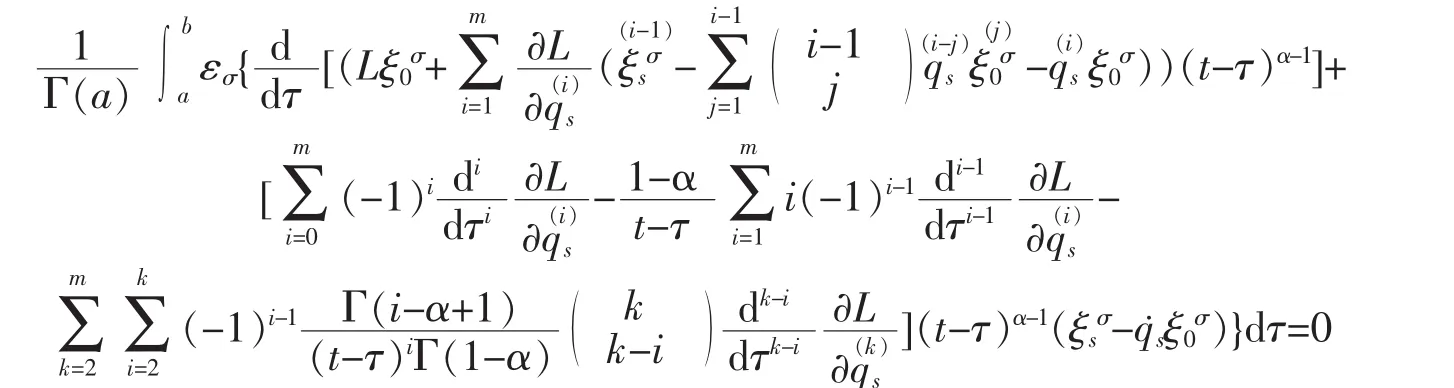
substituting formula(2) into the above equation,and considering the integral[a,b]is arbitrary and εσare independent,we obtain

Integrating the equation above,we have the conserved quantity (25).
Theorem 2If the infinitesimal transformations of group(4) for HODS are the Noether quasi-symmetric transformations under Definition 2,then the systems exist r linear independent conserved quantities,which are

ProofAccording to Definition 2,combining the formula (16) and (2),and considering the arbitrary of integral[a,b]and the independent of εσ,Theorem 2 will be proved.
Theorem 1 and 2 can be called Noether theorems of HODS based on ENFM.If we can find a Noether symmetric transformation or a quasi-symmetric transformation of the system,then we can get a corresponding conserved quantity.
2.3 Perturbation to Noether symmetries and adiabatic invariants
Definition 3Ifis a physical quantity of HODS based on ENFM including v whose highest power is z,and its derivative with respect to τ is directly proportional to vz+1,then Izis called a zth-order adiabatic invariant of the system.
Suppose that the system we discussed given by equation(2) is disturbed by small perturbation vQs,and the original symmetries and invariants of the system will be changed accordingly.The equations of motion of the system disturbed by the perturbation will become

Assume that the disturbed generatorsare small perturbation to the generators of symmetrical
transformations of undisturbed systems,and we obtain

then we have
Theorem 3For HODS based on ENFM given by equations(2)which is disturbed by small perturbation vQs,if there is a functionthat makes the generatorsof infinitesimal transformations satisfy the following structure equations


is a zth-order adiabatic invariant of the system.
Proof
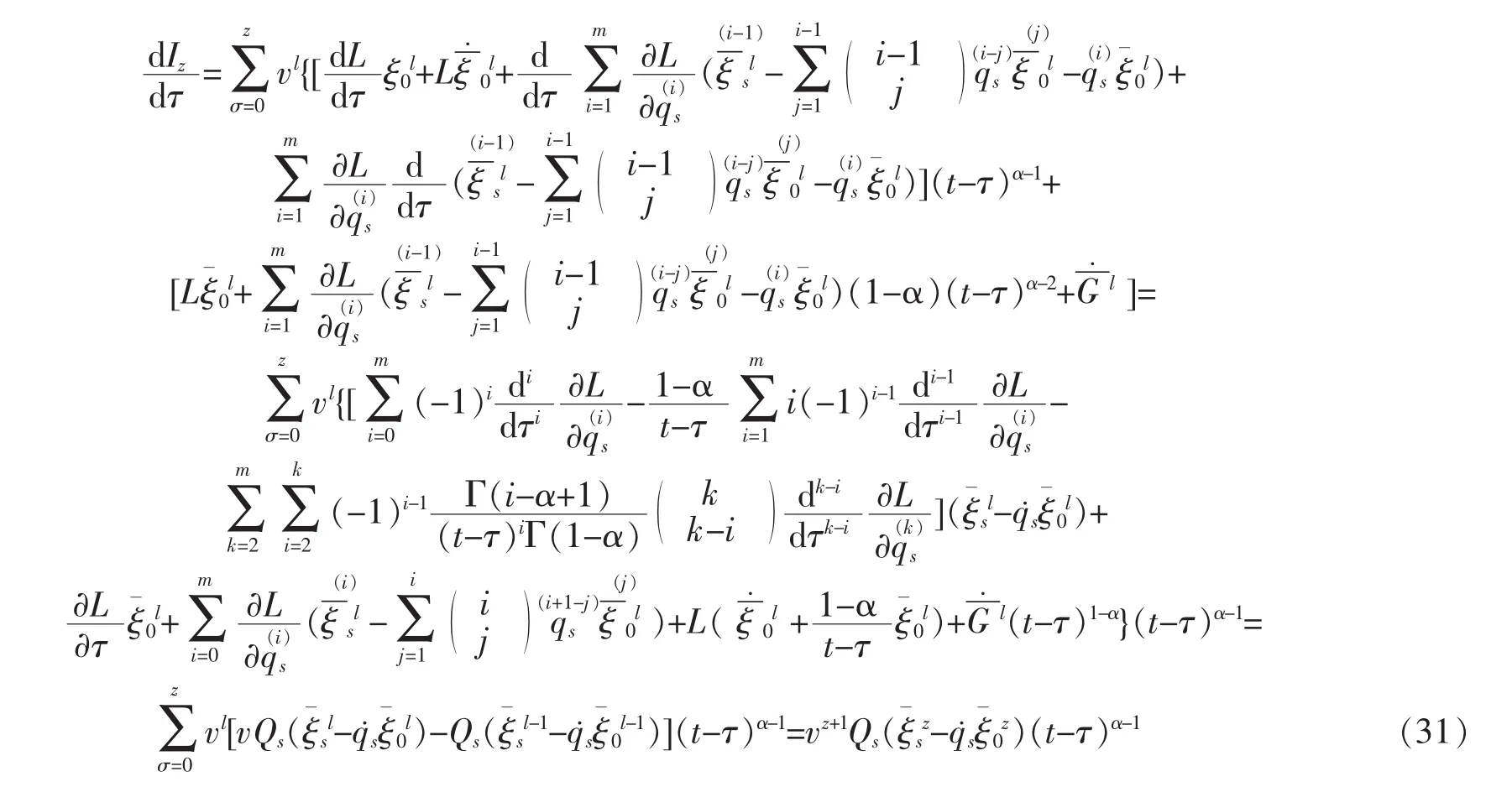
So Izis a zth-order adiabatic invariant of HODS based on ENFM.
3 An illustrative example
We illustrate an example to demonstrate effectiveness and validity of the new model we discussed above,ENFM.
Suppose that the generalized El-Nabulsi-Hamilton action of HODS is

First let us seek the exact invariant of the system.According to Noether identity given by equation (23),the 2nd-order Noether identity will be
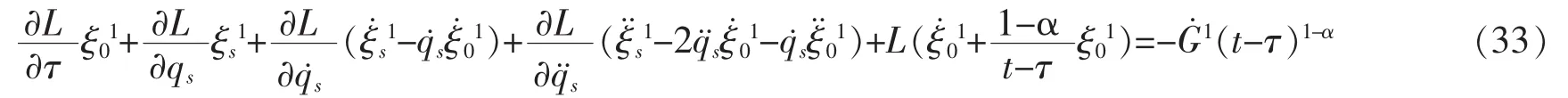
the Noether identity (33) gives
Equation (34)has a solution

According to Theorem 1,the system has an exact invariant as follows

Suppose that the system is disturbed by the following small force of perturbation

Let m=2,the structure equations (29) will be
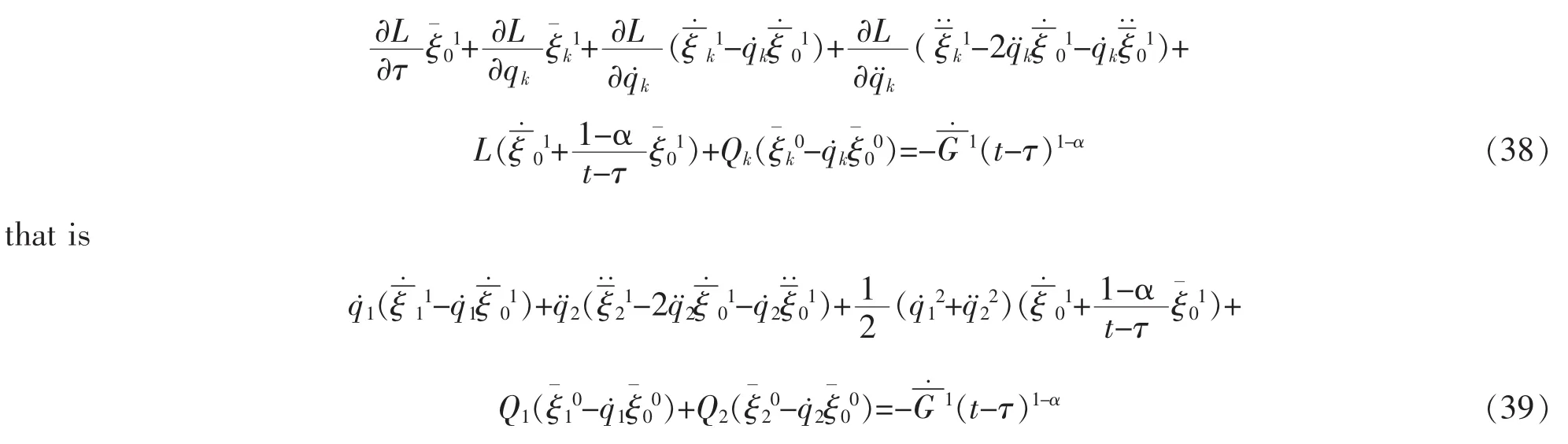
equation (39) has a following solution
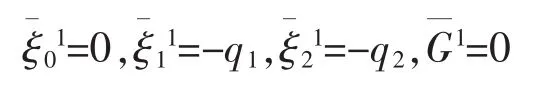
According to Theorem 2,we obtain a first-order adiabatic invariant of the system as follows

Furthermore,the higher order adiabatic invariants can also be obtained.
4 Conclusions
Based on ENFM,the relationship between Noether symmetries and exact invariants as well as perturbation to Noether symmetries and adiabatic invariants for HODS is proposed.The generalized El-Nabulsi-Euler-Lagrange equations are established and the two basic formulae of the variation of generalized El-Nabulsi-Hamilton action are derived.The definitions and criteria of Noether symmetric transformations and the quasi-symmetric transformations are given,and the exact invariants led directly by Noether symmetries are obtained.By introducing the concept of high order adiabatic invariant,the relationship between the perturbation to Noether symmetry and the adiabatic invariant of the system disturbed by a small force of perturbation is studied.The results of this paper are universal and significance,further work could include the extension of various constrained systems.

