基于图论方法的耦合系统稳定性分析

柴文慧

(山西管理职业学院，山西 临汾 041051)

引言

科学与工程设计应用中存在非常多的复杂网络，环境噪声的干扰是影响网络稳定性的重要因素，常见的噪声包括电报噪声、白噪声等。用随机微分方程描述的耦合系统来表示随机环境下的加权复杂网络，将其称为网络上的随机耦合系统，分析噪声和耦合系统稳定性之间的关系，能够进一步丰富复杂网络的相关理论，拓展随机微分方程理论的应用范围，同时有助于人们认识复杂网络，为后续更加深入的理论研究提供支撑。

1 基本理论及概念

1.1 图论概念

图论概念是应用数学中非常重要的一部分，曾有多位数学家独立建立过图论方法。图由顶点和边组成，是表示物件与物件之间的关系的方法。在其他的术语中，图也被称作网络，顶点被称作结点，边被称作链接。图的数学表示为：G=(V,E)，其中V表示的是顶点集合，E表示的是边集，图的一条边连接两个顶点，可以认为是顶点相连[1]。

无向图：在G=(V,E)中，如果对于任意的顶点存在a,b∈V，当(a,b)∈E，必有(b,a)∈E。

有向图：在G=(V,E)中，如果对于任意的结点存在a,b∈V，当(a,b)∈E，(b,a)∈E不一定成立，那么将其称为有向图。

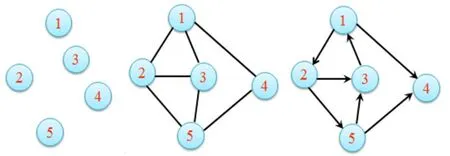
图1 图的顶点、无向图、有向图

可以利用序列表示结点之间的路径，路径上边的数目减去1即为路径的长度，如果一条路径除了其起点和终点相同外，其他的结点都是不同的，那么可以将其称为简单路径。

1.2 预备知识

耦合振子在工程领域中占据非常重要的地位，是一种应用广泛的耦合系统。在耦合系统应用过程中，随处可见的噪声干扰，可以利用图论方法和随机微分方程理论相结合的方式研究不同噪声干扰时耦合系统的稳定性。

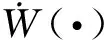
引理1：假设存在n≥2，那么下式成立：

Tk表示的是图G=(V,A)中以顶点为根生成树状结构的集合，w(Γ)表示的是Γ的权重。

引理2：假设存在n≥2，那么下式成立：

上式中，Fkh(xk,xh)表示的是任意的一个函数，表示的是图G=(V，A)中所有单圈图的集合，W(Q)表示的是权重，CQ是图的有向圈。

2 基于图论的带时交延迟随机耦合振子的稳定性分析

在实际的网络模型中，必须充分考虑网络状态变量的变化率，所以此处重点分析中立型微分方程，它在金融市场分析、自动化控制、种群生态学等多个领域都有非常广泛的应用[3]。在下列模型中，同时考虑中立型时滞和耦合时滞，用图论分析方法和Lyapunov稳定性理论相结合的方式讨论耦合振子稳定性[4]。

2.1 模型的建立

顶点系统的振子方程可以表示为式2-1：

(2-1)

四个振子共同构成的耦合振子网络可以表示为图2：

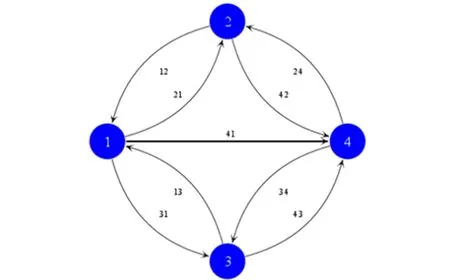
图2 耦合振子系统示意图

假设耦合振子系统中共有n个振子，可以用式2-2表示耦合振子：

(2-2)

此处考虑到振子的时变延迟，转变后的中立型耦合振子网络可以表示为式2-3：

(2-3)

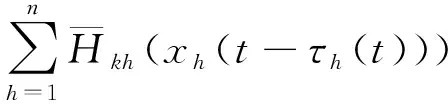
(2-4)

令yk(t)=dxk(t)/dt+ηxk(t),η>0，式(2-4)可以进一步改写为：

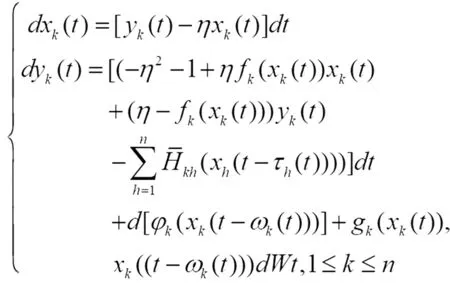
(2-5)

为了简化式子2-5，特设定：

Xk(t)=(xk(t),yk(t))T

Φk(Xk(t-ωk(t)))=(0,φk(xk(t-ωk(t))))T

Fk(Xk(t))=(yk(t)-ηxk(t)),((-η2-1+ηfk(xk(t))xk(t)+(η-fk(xk(t)))yk(t))T

Gk(Xk(t),Xk(t-ωk(t)))=(0,gk(xk(t)),xk((t-ωk(t))))T

式子2-5可以简化的表示成为式2-6：

d[Xk(t)-Φk(Xk(t-ωk(t)))]

(2-6)

2.2 Lyapunov-型稳定性定理

结合图论与Lyapunov稳定性理论[5,6]，对式(2-6)中的矩指数稳定性进行研究。首先做出如下假设：

假设1：时变延迟τk(t)和ωk(t)(1≤k≤n)满足下列各项条件

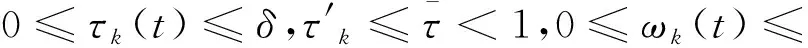
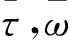
假设2：φk(0)=0，并且存在一个常数K，K∈(0,1)，满足

|φk(x)-φk(y)|≤K|x-y|,x,y∈，1≤k≤n

(2-7)

耦合系统(2-6)的初值条件可以表示为下式：

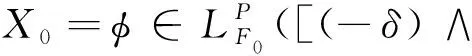
(2-8)

由文献[7,8]可知：假设Φk,Fk,Gk,Hkh满足固定的条件，那么耦合系统(2-6)的初值问题存在唯一的解。

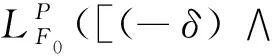
那么，可以认为耦合系统(2-6)的平凡解是满足p阶矩指数稳定条件的。

假设(CI)对于任意的值k,h(1≤k,h≤n)，存在常数μk,ξk,αk,βk,γhk,p≥2存在函数

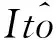
μk|Xk|p≤Vk(Xk)≤ξk|Xk|p

(2-9)

(2-10)

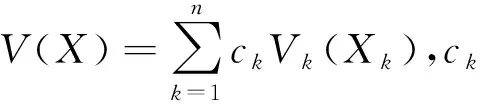
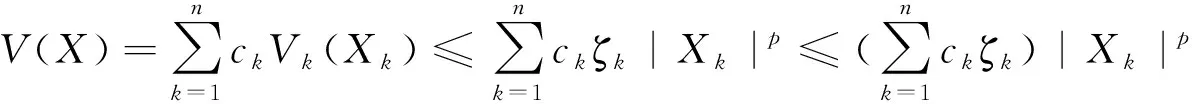
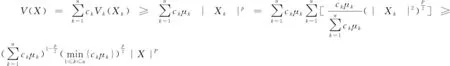
(2-11)

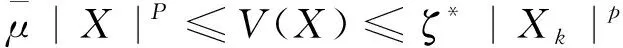
(2-12)

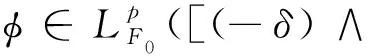
E‖φ‖p≤b0,a.s.

对于所有大于b0的整数b，σb=inf(t≥0:|X(t)≥b|)。

由此可以推导出：

(2-13)

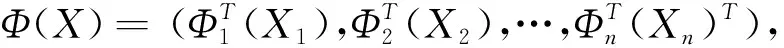
(2-14)

令b,σb→∞，那么可以推导出：

+2p-1Kpeδωeδ(t-ω(t))E[|X(t-ω(t))|p]

(2-15)

所以，对于任意存在的T>0，下列式子成立：

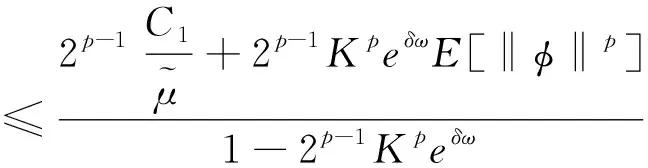
T→+∞，那么由此可以推导得出：

所以：

也就是说，式(2-6)的平方解为p阶矩指数稳定的。证毕。

3 总结

利用图论方法分析时变延迟中立类型随机耦合系统的稳定性，首先用有向图描述模型，在建立模型时考虑时滞和噪声干扰，然后利用图论方法，Lyapunov和稳定性定理相结合，得出耦合系统具有矩指数稳定性，并给出一个数值算例，验证系统稳定性。