由高考题例谈高中数学建模能力的培养

江苏省苏州市吴中区木渎金山高级中学 王 赟

《普通高中数学课程标准》中指出：数学建模是对现实问题进行数学抽象，用数学语言表达问题，用数学方法构建模型解决问题的素养。数学建模是应用数学解决实际问题的基本手段，也是推动数学发展的动力。数学建模主要表现为：发现和提出问题，建立和求解模型，检验和完善模型，分析和解决问题。

江苏高考卷一直在坚持以建模为主，“在考查基础知识的同时，侧重考查能力”是高考的重要意向，而应用能力的考查又是近二十年来的能力考查重点。应用题的载体很多，按考查的知识分类有：函数（一次、二次和三次函数以及分式函数、分段函数、三角函数等）型；不等式型；解三角形型；解析几何型等。2016、2017年应用考题是立体几何模型，2017年应用考题需利用空间中的垂直关系和解三角形的知识求解。

【例1】（2016·江苏高考）现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P-A1B1C1D1，下部的形状是正四棱柱ABCD-A1B1C1D1（如图所示），并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍。

（1）若AB=6m，PO1=2m，则仓库的容积是多少？

（2）若正四棱锥的侧棱长为6m，则当PO1为多少时，仓库的容积最大？

分析：本题考查柱体与锥体的体积计算方法，解题的关键是掌握柱体与锥体的体积计算公式，进而化成函数的概念、导数的应用，再结合导数知识解决相应最值问题。

解：（1）由PO1=2知O1O=4PO1=8。

因为A1B1=AB=6，

所以正四棱锥P-A1B1C1D1的体积

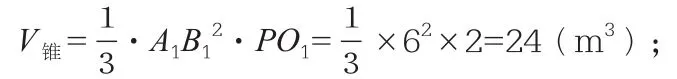
正四棱柱ABCD-A1B1C1D1的体积

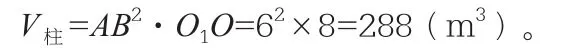
所以仓库的容积V=V锥+V柱=24+288=312（m3）。

（2）设A1B1=a m，PO1=h m，

则0＜h＜6，O1O=4h，连接O1B1，

因为在Rt△PO1B1中，O1B12+PO12=PB12，

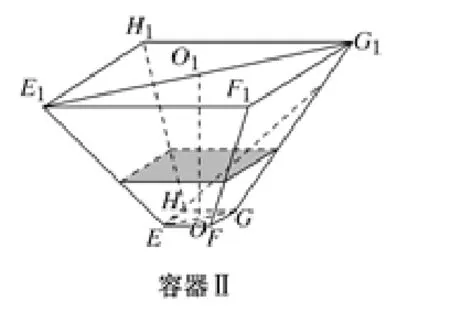
【例2】（2017·江苏高考）如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32 cm，容器Ⅰ的底面对角线AC的长为10cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm。分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12 cm。现有一根玻璃棒l，其长度为40cm。（容器厚度、玻璃棒粗细均忽略不计）

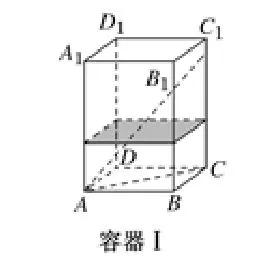
（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；

（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度。

分析：解三角形问题多为边和角的求值问题，这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系，从而达到解决问题的目的。其基本步骤是：

第一步：定条件，即确定三角形中的已知和所求，在图形中标出来，然后确定转化的方向。

第二步：定工具，即根据条件和所求合理选择转化的工具，实施边角之间的互化。

第三步：求结果。

解：（1）由正棱柱的定义知，CC1⊥平面ABCD，

所以平面A1ACC1⊥平面ABCD，CC1⊥AC。

如图，记玻璃棒的另一端落在CC1上的点M处。

记AM与水面的交点为P1，过P1作为垂足，

则P1Q1⊥平面ABCD，故P1Q1=12，

答：玻璃棒l没入水中部分的长度为16 cm。

（如果将“没入水中部分”理解为“水面以上部分”，则结果为24 cm）

（2）如图，O，O1是正棱台的两底面中心。

记玻璃棒的另一端落在GG1上的点N处。

则GK=OO1=32。

因为EG=14，E1G1=62，

于是 sin ∠ NEG=sin（π-α-β）=sin（α+β）=sin αcos β+cosα

记EN与水面的交点为P2，过P2作为垂足，则平面EFGH，

故P2Q2=12，从而

答：玻璃棒l没入水中部分的长度为20 cm。

（如果将“没入水中部分”理解为“水面以上部分”，则结果为20 cm）

对应用题的训练，一般从读题、审题、剖析题目、寻找切入点方面进行强化，注重培养将文字语言转化为数学语言的能力，强化构建数学模型的几种方法。应用题体现综合（在不同知识点交汇处编题），不断创新（问题的背景、设问的方式、解题的方法方面），强化能力（对考生的阅读理解能力、将实际问题向数学问题转化的能力、运用所学数学知识解决实际问题的能力）。

解答应用题关键是要过好三关：

（1）审（读）题关：读懂题意，明确问题的实际背景；审题时，抓住问题中的有用信息，理顺数量关系，为建模做准备。审题时要努力做到三读：粗读——细读——精读。

（2）建模关：确定问题模型，将实际问题数学化，明确本小题实际上是一个什么样的数学问题（已知什么？求什么？）。值得一提的是，由于一个大题有若干小题，因而对于题目提供的条件，在解每个小题时，要正确判断该用哪些条件。

（3）解模关：将应用问题转化为数学问题后，就要运用恰当的数学知识与方法去解决已转化了的数学问题：与图形有关的应用题应注意数形结合；与函数有关的问题应注意函数的性质运用，与不等式有关的问题要灵活运用不等式知识（如解不等式、运用基本不等式求最值等）。值得一提的是，几乎每年的高考应用题都有一个最优化问题，因而在解模中要熟练掌握求最值的几种常用方法。

通过高中数学课程的学习，让学生学会用数学的眼光来观察，用数学的思维来分析，用数学的语言来表达。除了通常讲的分析问题、解决问题能力，我们还强调学生要有发现问题、提出问题的能力，这其中有预判、预测、推演、找到巧妙的方法的过程，这才是数学思维的训练。提升学生核心素养，是落实教育本源的问题，也意味着教与学的方式都要转型。关注学生身心健康，长远发展，终身学习的能力，为学生走上社会打好基础，也就是“教是为了不教”。