酒瓶的摆放艺术

黄婉盈　宋晓辉　白玉军

研究动机

酒瓶摆放问题起源于文艺复兴时期。它的表述是这样的：在酒柜中摆放13个大小相同的酒瓶，如果在底层摆放3个酒瓶，并且其中2瓶紧贴两端，则依序放入13瓶酒后，一定会使最顶层的3瓶酒一样高。我越想越觉得有兴趣，但同时也怀疑这个问题是否正确。当我去询问老师的时候，老师建议我先找出其中的规律性，利用规律性再看是否能推导出其他的排列方式。于是，在老师的指导下，我开始对“13瓶酒”的问题进行研究，寻找摆放13瓶酒的方法是否唯一及其规律性，进而利用规律性推演出其他的相关摆放情况。

研究过程

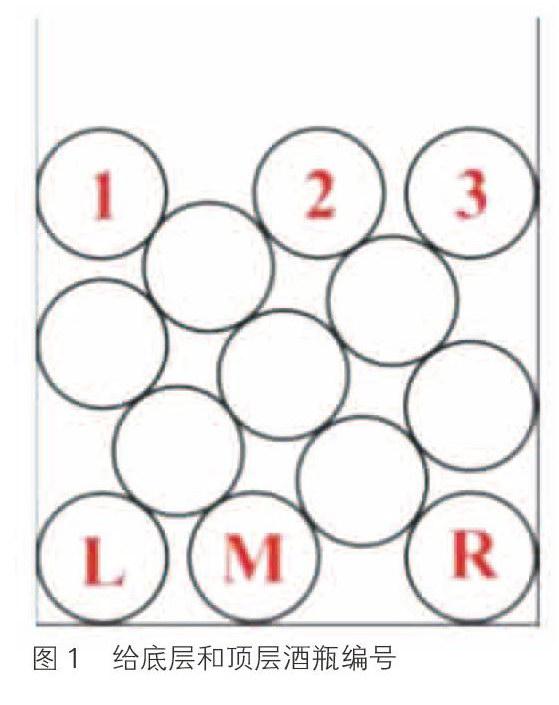
我们把底部的3个酒瓶各自给予一个名称：L代表左瓶，M代表中间的瓶子，R代表右边的瓶子。而最顶层的3个酒瓶，最左边的称为1瓶，中间的称为2瓶，右边的称为3瓶，见图1。假设酒瓶的直径为r。

估计酒柜的宽度

因为最底层能摆放3瓶酒，所以酒柜的宽度最少要等于3个酒瓶的直径；而为了让M瓶有可以移动的空间，所以最大宽度不可以超过4个酒瓶直径的宽度（否则上层的酒瓶就会滚落到最底层）。

结论：3r≤酒柜的宽度<4r

以自制的酒瓶模型（同面值硬币）与酒柜模型（白板）寻找可能出现的情况

酒柜宽度是3瓶酒的宽度：只有1种排列方式，经过目测，看起来是等高的。

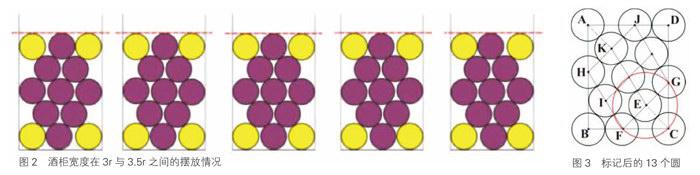
酒柜宽度在3r（不含）与3.5r之间，可以归纳出5种排列方法，分别是L跟M相接触、M在中间偏左、M在正中间、M在中间偏右和M跟R相接触。经过目测，每一组看起来都是等高的，见图2。

以同样的方式观察酒柜宽度刚好为3r的宽度和酒柜宽度在3.5r与4r（不含）之间的11种摆放情况，经过目测，每一组看起来都是等高的。在全部这16种情况中，可观察到一个共性：

若M紧贴着L，则2会紧贴着3；当M向R移动时，则2也会逆向地往1移动；若M跟R紧贴，则2就会跟1紧贴。

确定最顶层的3瓶酒是否真的等高

观察图2可发现，除了固定不变的4瓶外，其他9个瓶子将形成一个四边形的形状；现在我们随意取一组出来，并且将所有的圆都标上圆心，之后把外面代表酒柜的框涂掉，接着把中间的9个圆心连线，另外把固定不动的4个圆的圆心分别与旁边的圆心相连接，最后再把圆心标上字母，见图3。

在图3中，连接CE，因为CE、EF和EG都等于酒瓶的直径r，所以我们可以知道，C、F、G这3个点都会落在以E为圆心且半径为r的圆周上，再加上∠FCG=90°，于是可以知道：F、E、G这3点恰好在同一条直线上。同理，H、I、F这3点也在同一条直线上，可以推导出四边形HFGJ是一个菱形。

再连接AK，因为AK、KH和KJ都等于酒瓶的直径r，所以A、H、J这3点都会落在以K为圆心且半径为r的圆周上，又因为H、K、J这3个点在同一条直线上，所以可以知∠HAJ=90°。同理，可以得到∠JDG=90°。因此，可以证明四边形ABCD正好为一个长方形。由于四边形ABCD为一个长方形，所以可知道A、J、D这3点在同一条直线上，并且和BC平行，也就是这3点将会在同一高度上。既然圆心都在同高度上，那么这3个酒瓶当然也就等高了。用相同的方法，在其他组也可以证实最顶端的3瓶酒一定会等高。

结论：不管怎么排列，最顶端的3瓶酒1、2、3一定会等高。

继续向上堆，是否有某一层的3瓶酒能够等高

经推导证明（过程略），只要是对称组组合，每增加10瓶，就可以保持顶层的酒瓶等高；在特殊情况下每增加5瓶，同样也可以保持顶层的酒瓶等高。

若将酒柜的宽度延伸，是否会有等高的情形发生

观察前面图形我发现，堆好的瓶子是类似长方形的排列，若是将堆好的瓶子旋转90°，就可以发现：每次底层增加2瓶，则总瓶数将增加10瓶。

如果再继续向上堆，是否会有等高的情形发生

经推导证明（过程略）：底层为奇数时，若是继续向上堆去，则每次将增加（第一次等高的瓶数-底层的瓶数）瓶；底层为偶数时，若是继续向上堆去，则每次将增加（底层的瓶数×2-1）瓶。

研究结论

基本型：底层保持只有3瓶，向上堆时，第n次顶层的一样高，则需要（10n+3）瓶（n为正整数）；特殊情况（底层M瓶在正中间时）第n次顶层的一样高，则需要（5n+8）瓶（n为正整数）。

推广型：底层向右边增加，底层瓶数分为奇数和偶数2种情况。底层为奇数时，底层为（2m+1）瓶，第1次顶层一样高，则需要（10m+3）瓶（m为正整数）；底层为偶数时，底层为2m瓶时，第1次顶层一样高，则需要（10m-2）瓶（m為正整数）。

最终型：底层向右增加，第n次等高时，若底层为奇数，底层为（2m+1）瓶，第n次顶层一样高，则需要（8mn+2m+2n+1）瓶（m、n都是正整数）；底层为2m瓶时，第n次顶层一样高，则需要（4mn+6m n 1）瓶（m、n都是正整数）。

该项目获得第32届全国青少年科技创新大赛创新成果竞赛项目中学组数学一等奖。

专家评语

本项目应用初中几何知识证明了摆放13瓶酒方法的唯一性和规律性，其次应用翻折、数学归纳等方法将问题推广，分别得到底层为奇数或偶数瓶时第n次等高摆放的酒瓶数，具有独创性。项目立意有创新，研究方法合理，论据充分，研究成果有说服力。建议将得到的3种类型结果之间的联系指明，并考虑研究方法是否可推广到其他问题（例如地砖问题）中。