猜想，为解题探寻方向（一）

沙国祥

2016年高考结束几天后，一位考生来到《新高考》编辑部，我问他：

“第19题第（2）小题（附后），你当时是怎么想的？”

（2016年江苏卷第19题）已知函数f（x）=ax+bx，（a>0，b>0，a≠1，b≠1）.

（1）略：

（2）若Ol，函数g（x）=f（x）-2有且只有1个零点，求ab的值.

“我是先猜出 ab=l的，这时g（x）=ax+a-x-2，它的图象关于y轴对称，x=o是g（x）的唯一零点.”

从直观上看，偶函数f（x）的图象（如图1是a=0.5时f（x）的图象）具有轴对称性，且在x=O时f（x）的图象在最低点处与直线y=2相切，这意味着x=0时，g（x）的图象在最低点处与x轴相切，据此可猜想题目的结论，从而为下一步证明找到方向和思路：

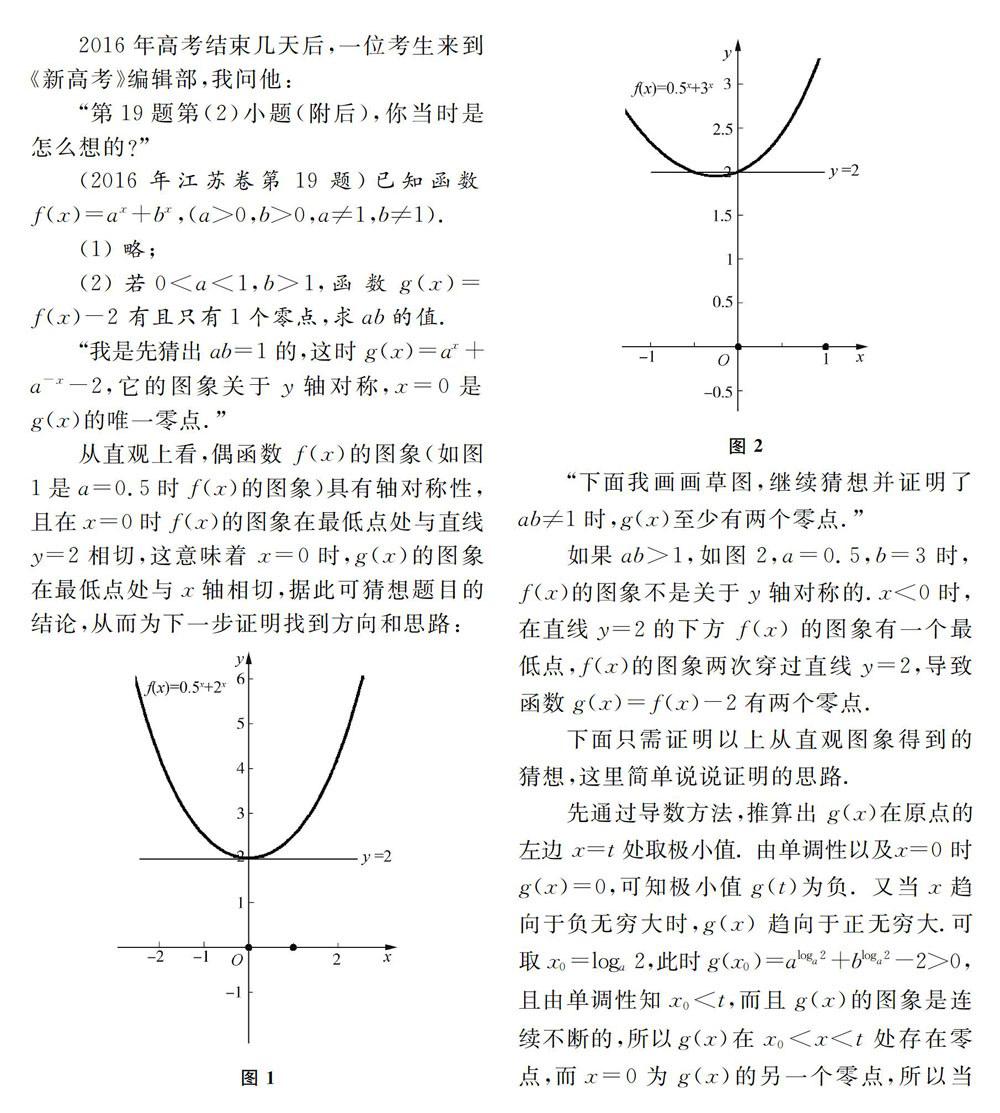
“下面我画画草图，继续猜想并证明了ab≠1时，g（x）至少有两个零点.”

如果ab>l，如图2，a=0.5，b=3时，f（x）的图象不是关于y轴对称的.x

下面只需证明以上从直观图象得到的猜想，这里简单说说证明的思路.