基于逐步优化的轨道交通网络行车计划衔接

李 伟，罗 钦

1) 深圳大学光电工程学院，光电子器件与系统教育部/广东省重点实验室, 广东深圳 518060；2) 深圳技术大学城市交通与物流学院，广东深圳 518118

随着城市轨道交通的不断发展，城市轨道交通运营管理逐步进入网络化运营阶段，直接体现在网络中不同线路间的换乘衔接．良好的换乘衔接会缩短乘客的换乘等待时间，提升乘客的轨道交通出行良好感受，相反糟糕的换乘衔接则会大大延长乘客的换乘时间，降低轨道交通的服务水平．因此，在研究制定城市轨道交通列车行车计划时应尽可能缩短乘客在路径上的换乘等待时间．行车计划的主要内容包括该时段的列车开行间隔以及换乘站换乘衔接方案．

传统意义上的行车计划优化是指在满足众多运营和安全约束(如到达或出发间隔要求)的条件下，生成一个使目标函数可行或使给定目标函数较优的列车运行图．列车运行计划优化问题是一个典型的NP难(non-deterministic polynomial-time hard)问题[1-3]，不少学者利用如启发式算法[4]、分支定界法[5-6]、仿真方法[7]及衔接分层优化算法[8]等求解该优化问题．然而，随着客流在制订轨道交通列车行车计划、合理配置运能方面的指导作用日趋重要，如今优化模型的目标函数不仅局限于轨道交通运营层面．文献[9-11]通过引入动态客流需求研究行车计划衔接与优化问题，以时变客流需求为背景，以乘客在车站的候车时间最小化为目标函数，利用启发式算法求解列车运行计划优化问题．

以上增加时变客流因素的研究大大增加了列车运行计划编制的科学性和先进性．然而，当前中国许多大城市的轨道交通网络规模十分庞大，线路及换乘站数量多，换乘方向繁多复杂，各线路间、各换乘站内部的关系具有关联和不确定性，若将网络上所有换乘站均考虑在内，求解起来十分困难，使用常规的建模及优化方法分析该问题已无法得到满意结果，较难用于实际．因此，研究一个贴近实际并且易于实现的行车计划衔接优化模型显得尤为重要．

面对一个具有复杂关系和众多参变量的大系统，需从系统内部相互关联子系统的分解出发，逐步、逐级地研究．基于以上考虑，本研究探讨在时变客流需求下的网络行车计划衔接优化问题，采用逐步优化思想，优先考虑换乘客流大的车站和衔接方向，并依次考虑换乘客流小的衔接方向，逐步形成优化的列车运行计划．该问题可以被阐述为：以具体客流需求数据为基础，以列车开行间隔与列车到达时刻为变量，以整体换乘衔接为目标函数的优化模型，旨在减少乘客总候车时间及提升轨道交通运营服务频率与运营服务水平，提升轨道交通整体网络动态可达性．

1 换乘站的主动衔接与换乘衔接

轨道交通换乘衔接优化模型的主要思路为：参考最小生成树思想，先对换乘站换乘衔接方向按客流量大小排序，优先考虑换乘站换乘客流大的衔接方向，并综合考虑同一换乘站内相关换乘衔接方向，以平均换乘等待时间为目标函数进行局部优化求解，逐步求解得到全网络所有换乘站的优化列车行车计划．

在此之前，先提出主动衔接与被动衔接概念，由于同一换乘站内，换乘衔接方向A-B的产生就必然会有换乘衔接方向B-A，调整线路A和B任意的列车开行间隔和到达时刻均会导致这两个换乘衔接方向乘客的换乘等待时间发生改变，因此，线路A和线路B之间换乘衔接就存在主动衔接和被动衔接概念，由线路A去主要衔接线路B称之为主动衔接，相应线路B衔接线路A称为被动衔接．定义符号⎣*」表示不大于*的最大整数，「*⎤表示不小于*的最小整数．

1.1 主动衔接平均换乘等待时间

假设主动衔接方向为由线路换向线路，换乘路径的示意图如图1．

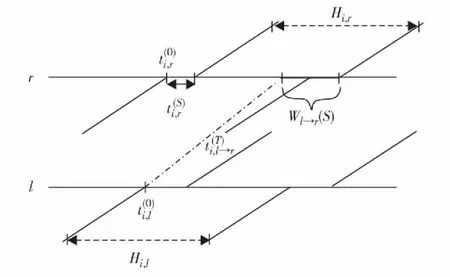
图1 主动衔接示意图Fig.1 Active coordination of transfer connection direction

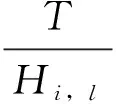
(1)

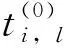
同时，可得线路r上列车在车站的发车时间为

(2)

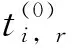
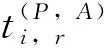
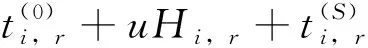
(3)

整理可得

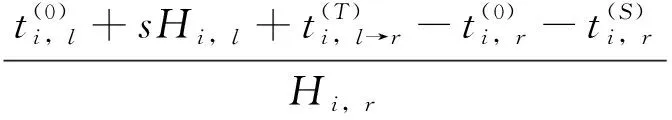
(4)

考虑到理性乘客首选候车后第1趟到达的列车，则

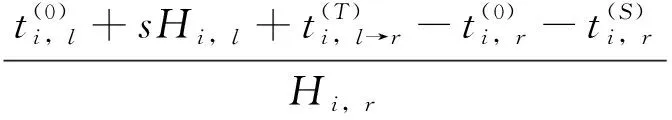
(5)

因此，第s列列车上乘客的换乘等待时间Wl→r(S)为

(6)

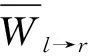
(7)

1.2 被动衔接平均换乘等待时间

主动衔接方向为由线路l换向线路r， 相应被动衔接方向为线路r换向线路l， 对应的换乘示意图如图2．其平均换乘等待时间的计算方法与主动衔接平均等待时间的计算方法相类似．

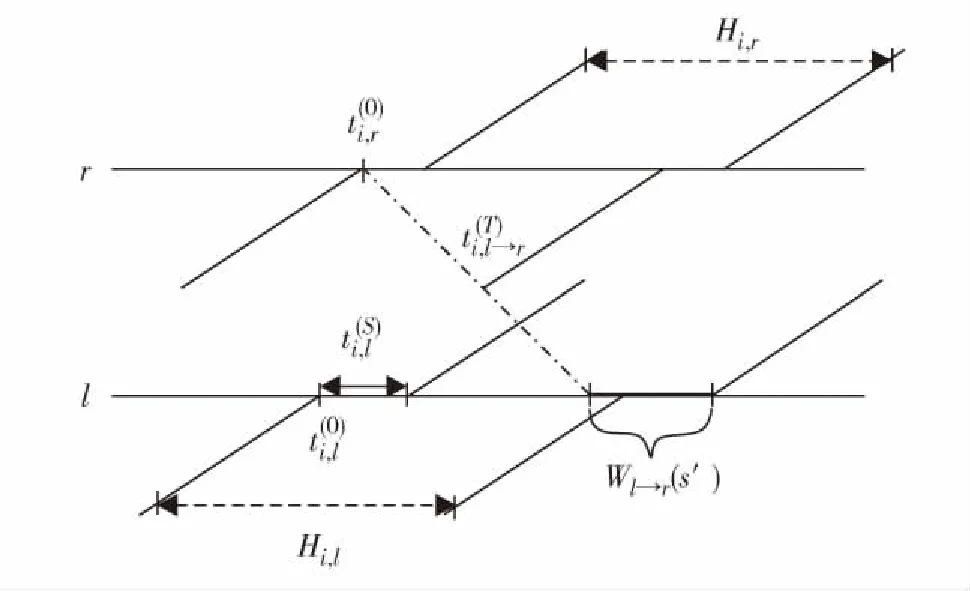
图2 被动衔接示意图Fig.2 Passive coordination of transfer connection direction

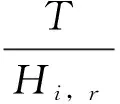
(8)

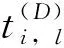
(9)

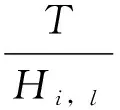
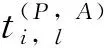
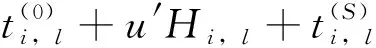
(10)

整理可得

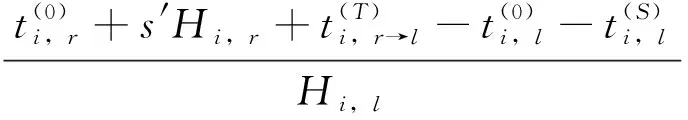
(11)

考虑到理性乘客第一选择始终是候车后第一趟到达的列车，因此

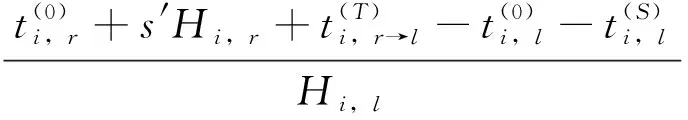
(12)

则第s′列列车上乘客的换乘等待时间Wr→l(s′)可以表示为

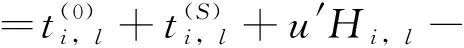
(13)

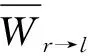
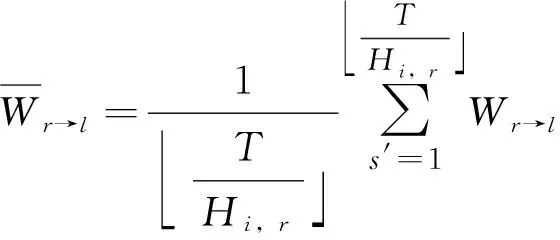
(14)

1.3 总平均换乘等待时间

综合主动衔接和被动衔接两个平均换乘等待时间，在车站i的总换乘等待时间F为

(15)

其中，fi,l→r(T)为在时间段T内，在车站i中从线路l换向线路r的总客流量；fi,r→l(T)为在时间段T内，在车站i中从线路r换向线路l的总客流量．

要求换乘车站i的主动衔接方向和被动衔接方向的衔接程度最优，即使得总平均换乘等待时间最小，需满足

(16)

s.t.Hmin,l≤Hi,l≤Hmax,l

Hmin,r≤Hi,r≤Hmax,r

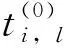
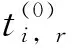
其中，Hmin,l和Hmin,r表示列车开行间隔能取的最小值，其与线路折返能力、追踪能力有关；Hmax,l和Hmax,r表示列车开行间隔能取的最大值．

2 逐步优化求解算法

模型求解思路主要基于逐步优化思想，① 将换乘站换乘衔接方向按换乘客流大小排序；② 对换乘客流大的衔接方向优先构建连接边，确定该方向列车开行间隔和列车到达时刻，并进行标记，逐步按换乘客流大小依次将网络上所有换乘方向覆盖，形成一个完整列车运营计划．具体求解思路的流程框架如图3．

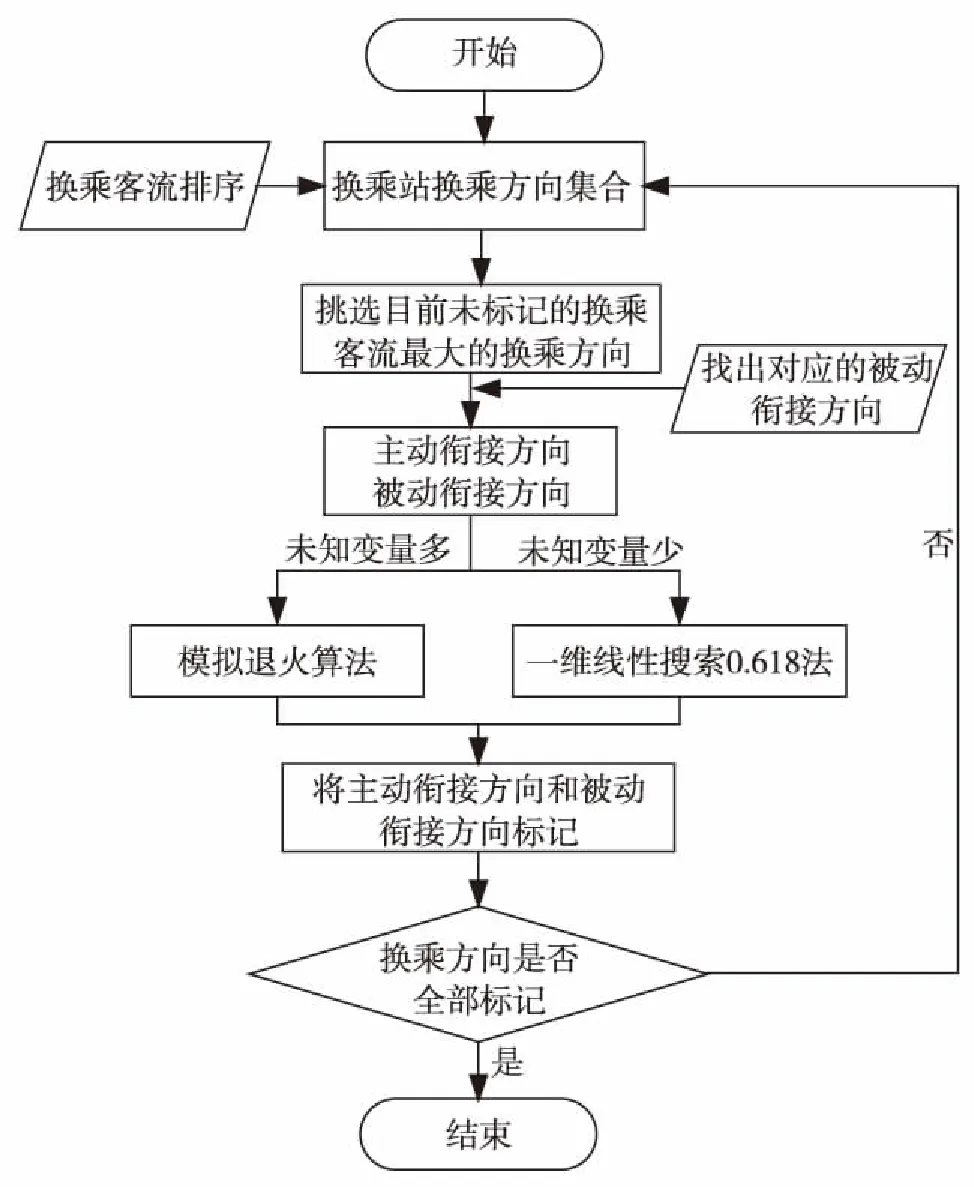
图3 算法流程图Fig.3 Algorithm flow chart

2.1 换乘客流排序

模型求解首先要得到按换乘客流量排序的全网络换乘衔接方向．得益于近来兴起的轨道交通自动售检票系统(automatic fare collection, AFC)，我们可以获得大量乘客出行数据，进而获得在微观层面上量化的客流时空分布结果．具体使用方法为利用给出的路径清分比例表，分析计算指定日期和指定时间段的进出站AFC刷卡数据，可得每个时间点和每个车站上的客流量，随即获得该时段内各换乘站各换乘方向的客流量．将排序后的换乘站和换乘方向集合存储供后续步骤调用．

2.2 逐步优化

逐步优化目标可描述为：① 制定一个列车行车计划，使所有换乘站的所有换乘方向均能被接上，且网络所有换乘站的总换乘等待时间最小．根据排序好的换乘衔接方向，对换乘客流大的换乘衔接方向优先构建衔接计划，确定该方向列车开行间隔和首列列车到达时刻，并将该换乘方向进行标记；② 按换乘客流大小依次将网络上所有换乘方向连接上．若该方向列车开行间隔和列车到达时刻已被标记，则无需改变它们；若该方向列车开行间隔或列车到达时刻有其中一个未标记确定，则求解之．最终形成一个完整的列车行车计划．

2.3 分级求解算法

换乘衔接求解中存在两种情况，一是主动衔接与被动衔接中4个变量(分别为列车开行间隔与列车到达间隔)均未知，或3个变量未知1个变量已知；另一种是主动衔接与被动衔接中2个变量未知2个变量已知，或1个变量未知3个变量已知．从建立模型的公式可以看出，模型为弱约束最优化问题，当变量数量过多时(如情况一)，将很难求出优化结果，此时通常采取启发式算法，本研究选取模拟退火算法求解；而当变量数量少时(如情况二)，为得到较优结果，可采用最优化理论求解，本研究选取一维线性搜索算法求解．

模拟退火算法源于固体退火原理[12]，将固体加温至足够高的温度，加温时固体内部分子随升温变为无序状呈现随机排列状态，而逐步降温时粒子渐趋有序．最后在常温时达到基态，内部分子以低能状态排列，固体达到某种稳定状态．

具体模拟退火算法步骤如下：

步骤1设定初始温度值T0， 初始状态解x， 计算其目标函数值E．

步骤2内部循环．

1)产生一个随机干扰，得到新解x′， 并计算其目标函数值E′．

2)计算内能增量ΔE， 若ΔE<0， 则接受新解x′， 设新解为当前解x←x′， 跳转步骤4)，否则跳转步骤3)．

3)若ΔE>0， 计算概率p=e-ΔE/kTi， 并随机生成一个0～1的均匀分布变量，用以判断是否接受新解，若接受则设新解为当前解x←x′； 否则保持原解x， 转步骤4)．

4)若满足内循环终止条件，跳出内循环；一般内循环终止条件取为连续若干个新解都没有被接受，即当前解保持不变若干次循环．

步骤3外部循环．

1)判断当前温度Ti是否满足终止条件，即Ti→Tmin， 其中，Tmin为目标温度，若达到终止条件，则终止算法，输出当前解为最优解；

2)设置当前温度为Ti→Ti×ε， 其中，ε为温度衰减参数，一般设置为0.99或0.98，跳转步骤2开始内部循环．

本研究采用的一维线性搜索中“改进0.618法”来计算模型求解中未知变量少的情况二．0.618法(又称黄金分割法)是美国数学家KIEFER[13]于1953年提出，属于分割法函数求极值方法，分割类方法仅需计算函数值，因此使用范围较广，尤其适用于非光滑及导数表达式复杂或写不出等情形．改进0.618法是针对目标函数是单峰函数，也就是目标函数为凸的情形的分割类方法，因其不要求函数可微，且每次迭代只需计算1个函数值，程序简单容易实现而被广泛采用．由于黄金分割法是以等比例0.618分割缩小区间的，因此，针对在实际问题中遇到的目标函数往往不是单峰函数的情况，它是一种近似最优方法．

3 案例分析

以上海轨道交通网络为例，对本研究提出的城市轨道交通行车计划衔接优化算法进行分析验算，以平峰时期(如13∶00—15∶00)的列车衔接进行说明．实例分析中所需的数据如下：

1) AFC刷卡数据．选用2014-12-09的客流刷卡数据，其中选用时间段13∶00—15∶00的客流，共有1 386 402条配对好的进出站AFC刷卡数据．

2) 清分比例表．共有119 918个起终点(origin destination, OD)对，总共有288 200条路径．

3) 换乘走行时间．各换乘站各换乘方向的步行时间，可从上海轨道交通运营公司票务部门获取．

3.1 换乘方向排序

按照换乘站换乘客流大小进行排序，可得如表1的换乘衔接方向．

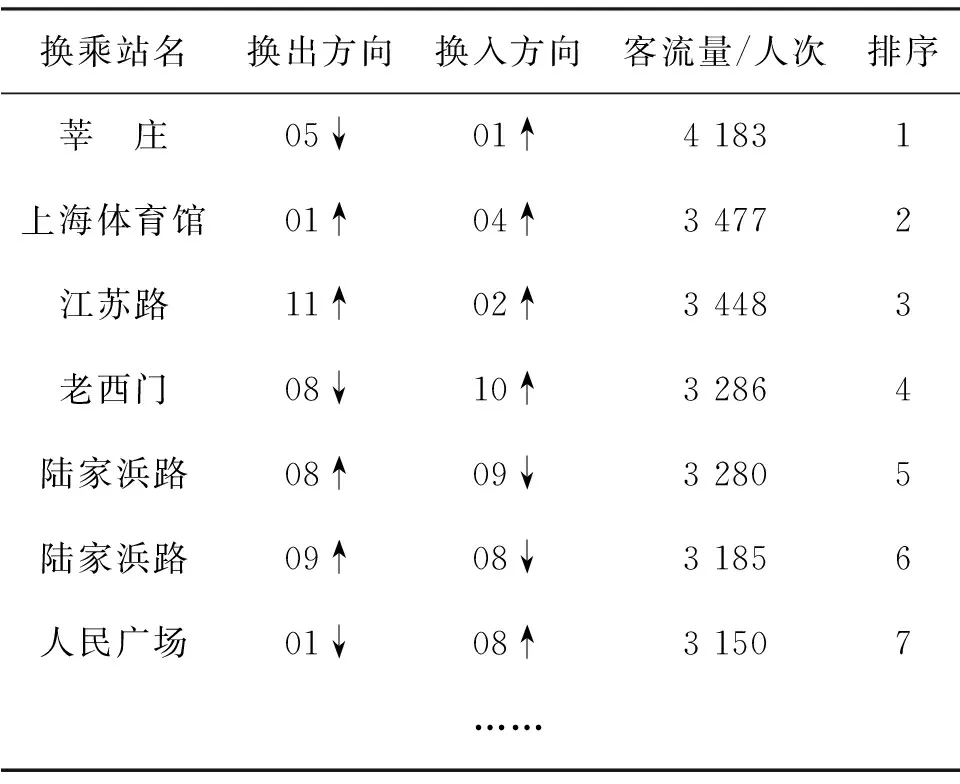
表1 平峰时期排序后换乘衔接方向示例Table 1 Examples of transfer connection direction ordered by passenger flow during flat period

3.2 优化求解

利用C#.Net程序语言对本节提出的模型与算法进行编程求解，按排序后的换乘衔接方向对换乘站换乘方向进行衔接优化，优化后进行标号，并依次处理余下换乘衔接方向，直至所有换乘衔接方向均已优化．优化过程如图4，其表示随程序求解步骤的推进，当前状态下网络平均换乘等待时间的改变程度．图中x轴表示程序求解步骤，即当前计算到排序后换乘衔接方向的顺序；y轴表示当前网络中已确定的模型决策变量数，包括列车开行间隔和首列到达时刻．图中数据散点圆的半径大小表示当前状态下网络平均换乘等待时间．数据点的大小随求解步骤的推移先增后减，说明随着换乘衔接方向的不断优化，乘客的平均换乘等待时间越来越优．

需指出，在图4程序求解步骤的后期，出现较长时间空白，原因在于该迭代时间点，换乘衔接的变量均在前面的求解步骤中被标定过，此步骤中无决策变量可求解，因此出现该数据点上的空白．

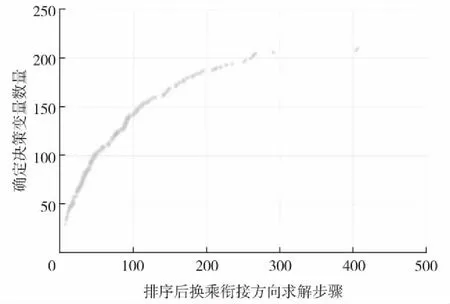
图4 求解代数-平均等待时间图Fig.4 Diagram of solving steps and average passenger waiting time

3.3 求解结果

最终获得所有换乘站换乘方向的衔接方案结果如表2．可见，平峰时段上海轨道交通1、2、4、5及11号线，由于存在换乘客流大的换乘站，其列车开行间隔优先得到衔接满足，而3、12、13及16号线，由于其中的换乘站客流较小，其列车开行计划主要用于衔接其他线路．此外，表2还显示，平峰时段线路上下行的列车开行间隔均保持相同，并且多条线路的开行间隔由于换乘衔接关系的密切，列车开行间隔呈相同或倍数的关系．同理，几个重要的换乘站首列到达时刻如表3．

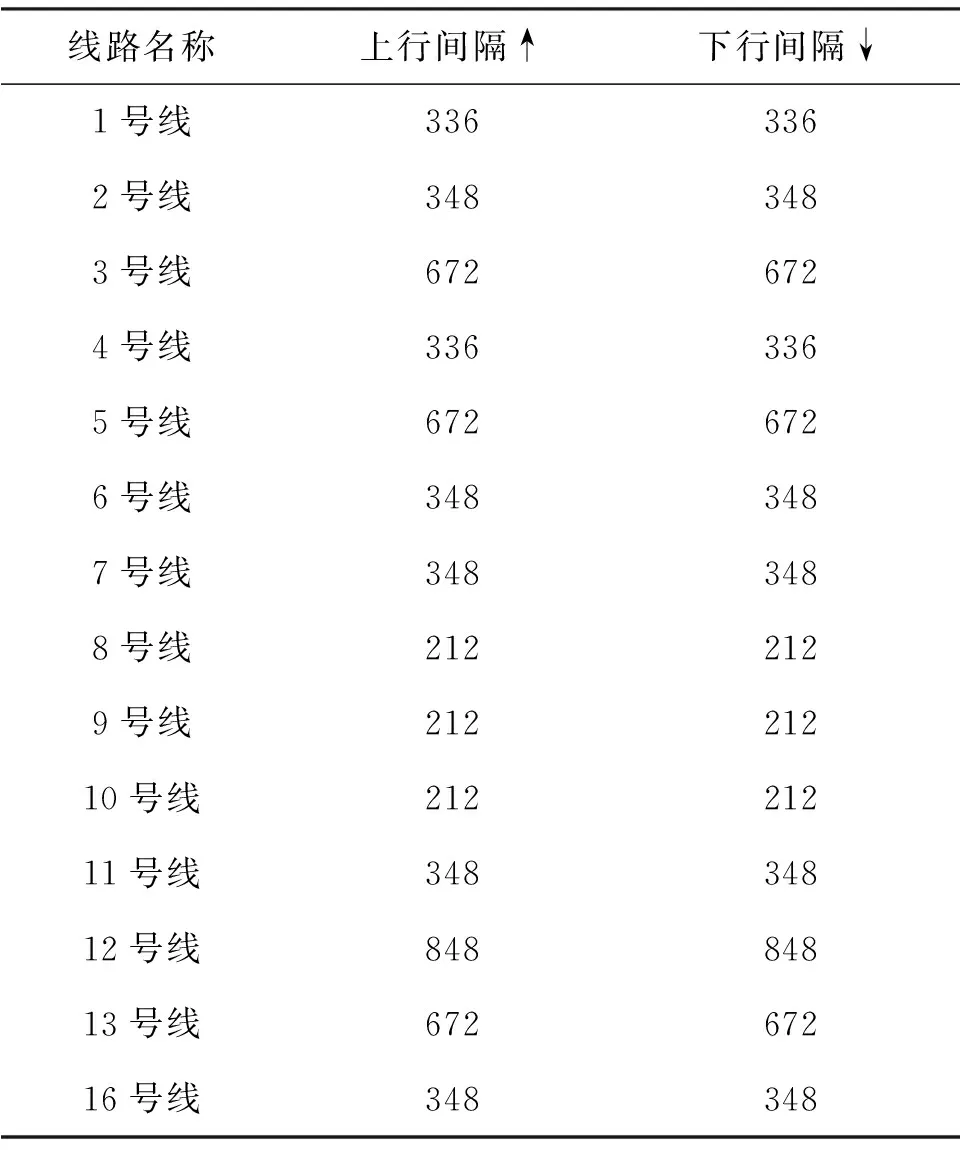
表2 优化后各线路开行间隔Table 2 Train interval of metro lines after optimization s

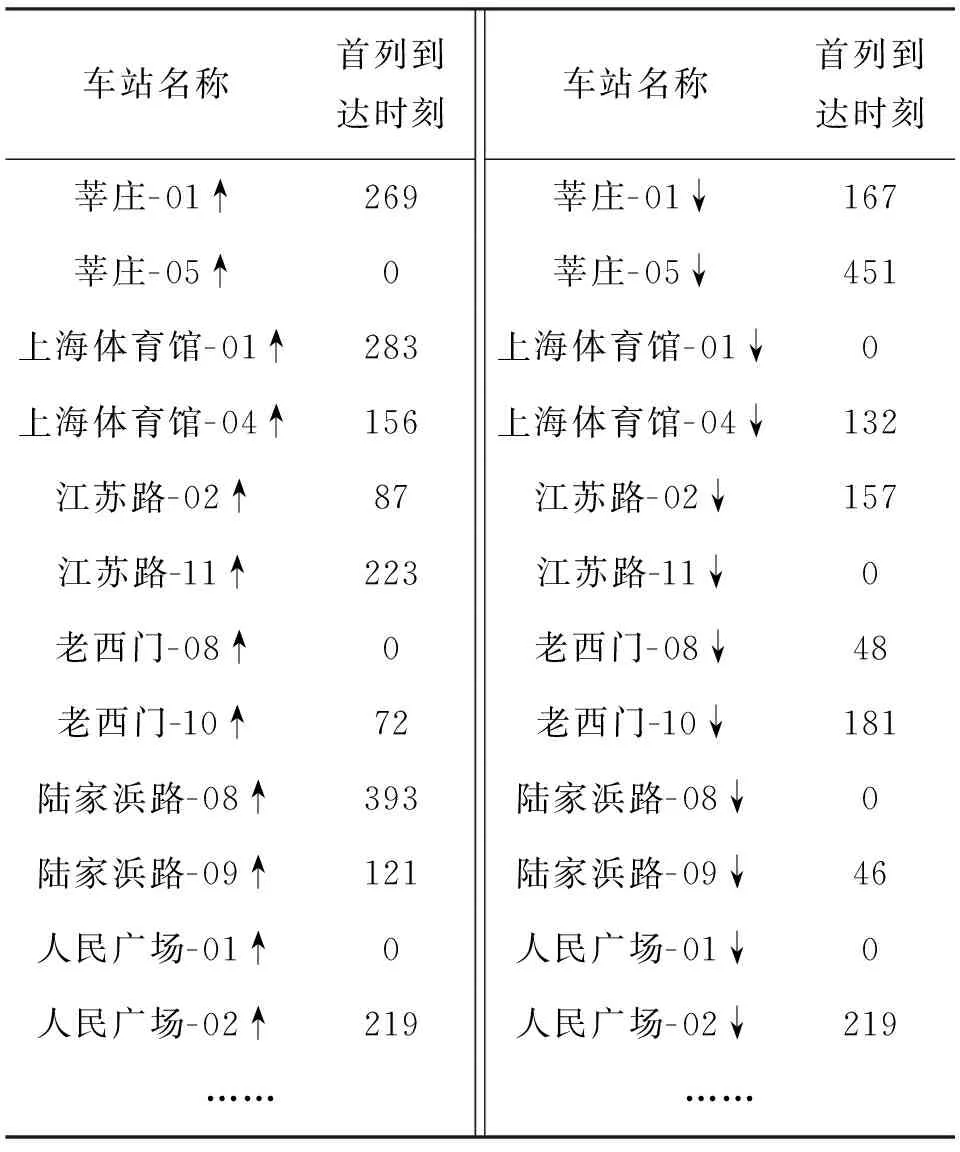
表 3 优化后各换乘站首列列车到达时间示例Table 3 First train arrival time of metro lines after optimization s

3.4 结果分析

本文研究时段为平峰时间段13∶00—15∶00，共计2 h，经计算共有换乘客流226 726人次，在未衔接优化之前，各线独立运营，未考虑相互之间的衔接关系，乘客的平均换乘等待时间为128.9 s．经优化衔接后，乘客的平均换乘等待时间为93.9 s，较之前平均减少换乘等待时间约27.1%，优化后的网络整体衔接效果较之前有一定提升．由此可见，通过调整线路间的换乘衔接关系，优化城市轨道交通网络整体衔接程度，可使乘客的平均换乘等待时间缩短，提升乘客出行效率，为网络上的出行乘客提供优质的客运服务．

结 语

本研究探讨常规时间下的城市轨道交通网络行车计划衔接优化问题，模型通过优化列车的开行间隔与列车的首列到达时刻，使乘客换乘站的总平均等待时间最短．建模中提出主动衔接和被动衔接概念，并利用它们计算换乘方向的总平均等待时间，并设计基于逐步优化的算法来解该模型．通过案例分析说明，本算法求解过程思路清晰，易于实现，能够优先匹配换乘客流量大的换乘衔接方向．且得出换乘衔接中，不同线路的列车开行间隔呈现相同或者倍数的关系，网络的整体衔接程度较优．