考虑土工膜缺陷的面膜坝渗透稳定性分析

，，，

(1.河海大学 水利水电学院，南京 210098；2.济宁市任城区水务局，山东 济宁 272000)

1 研究背景

复合土工膜是一类防渗性能好、施工方便、造价低、适应变形强[1]的防渗材料，被广泛应用于中低水头的库坝防渗工程。我国代表性面膜坝有西霞院土石坝工程、溧阳抽水蓄能电站等，国外有哥伦比亚的MielⅠ坝、美国的Olivenhain坝[2]等。但是，土工膜存在着容易老化、破损的特点，根据相关统计[3]，缺陷不均匀地分布在土工膜的不同部位。土工膜的缺陷会引起坝内水位线抬高、饱和区扩大、渗漏量变大等问题，在库水位骤降的情况下，容易导致上游坝坡出现失稳现象。

对于考虑土工膜缺陷情况下的土石坝渗流特性，许多学者进行了一定的探讨：孙丹等[4]基于饱和-非饱和理论对不同部位、不同尺寸的土工膜缺陷对渗流要素的影响进行了数值模拟；李传奇等[5]对清源湖水库土工膜防渗特性进行了分析，并考虑了土工膜破损的尺寸和部位的影响；沈振中等[6]对复合土工膜缺陷情况下进行了不同压力水头作用下的室内试验。但是对于此类问题的研究目前还不够完善[7]，尤其是在土工膜缺陷情况下，库水位骤降的坝坡稳定性研究还未见报道。鉴于此，有必要对土工膜破损情况下面膜坝的渗流特性、库水位骤降下的稳定性进行一定的探讨，对其中的规律展开分析研究。

本文以某面膜坝为例，研究了土工膜不同破损情况下的渗流特性，并讨论了库水位不同下降速率下上游坝坡安全系数的变化规律，为面膜坝的稳定性评价和治理提供了一定的参考。

2 渗流-边坡稳定耦合分析方法

2.1 饱和-非饱和渗流有限元分析理论

非饱和土达西定律写成张量的形式为

(1)

多孔介质渗流连续方程为

(2)

式中：xi为位置标识；ρ为水的密度；Q*为源汇项；n为孔隙率；Sw为饱和度。

将式(1)代入式(2)，并认为ρ为常数，考虑到θ与hc(压力水头)存在θ=θ(hc)，k(θ)=k[θ(hc)]，h=z+hc的关系(其中z为计算点的位置高程)，可以得到

(3)

于是可以得到以压力水头表示的饱和-非饱和微分方程为

(4)

式中：C(hc)为容水度；Ss为单位贮水量。

2.2 边坡稳定理论

边坡稳定分析采用19世纪50年代Bishop教授提出的Bishop法，Bishop法求安全系数公式为

(5)

式中：FS为安全系数，由迭代得到；c为土体黏聚力；β为滑块的底边长度；W为土条的重力；α为土条底面的倾斜角；φ为土体的内摩擦角；mα可以表示为

(6)

2.3 渗流-边坡稳定耦合

本文采用Geostudio分析模块中的Seep/W模块计算面膜坝不同工况下的瞬态渗流场，并将每个时刻不同的孔隙水压力导入Slope/W模块进行上游坝坡瞬态稳定性分析，利用Bishop法通过软件自动搜索滑动面半径得出安全系数随时间的变化规律。

3 土工膜缺陷数值模拟

3.1 工程概况

某面膜坝建于深厚覆盖层上，防渗方案采用上游坝面覆盖复合土工膜并向上游延伸40 m，土工膜厚0.01 m。坝基高程为0.0 m，坝顶高程为28.0 m，上游坡坡度为1∶2.4，下游坡坡度为1∶1.6，坝体内部采用砂砾石堆筑，坝趾处设有排水棱体，正常蓄水位高程为22.0 m，死水位高程为5.0 m，下游水位高程为0.0 m。面膜坝典型断面如图1所示。

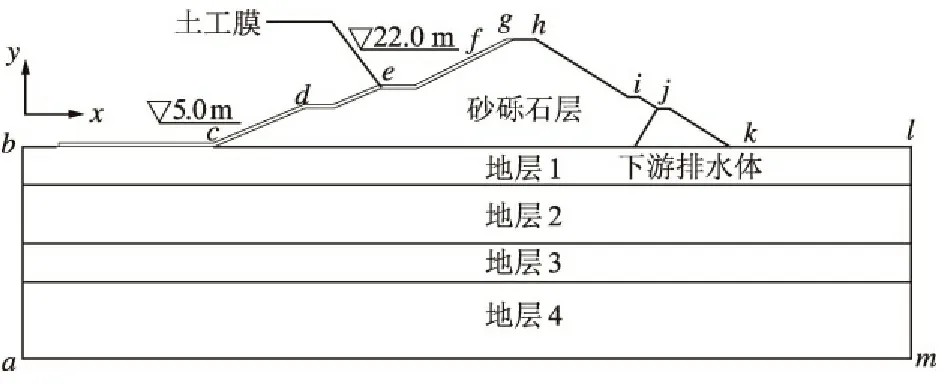
图1面膜坝典型断面
Fig.1Typicalsectionofgeomembranedam

3.2 材料参数

面膜坝各种材料物理力学参数见表1，土工膜由于尺寸较小，不易模拟，渗流计算采取文献[8]的方法对厚度以及渗透系数进行等效转换，土工膜破损模拟采用文献[4]的方法，即赋予破损土工膜一个较大的渗透系数，以模拟强透水情况，本文取值为10 m/s。

非饱和渗透系数方程采用Fredlund-Xing[9]法，可以估算出各种材料的渗透系数曲线以及土-水特征曲线，如图2。

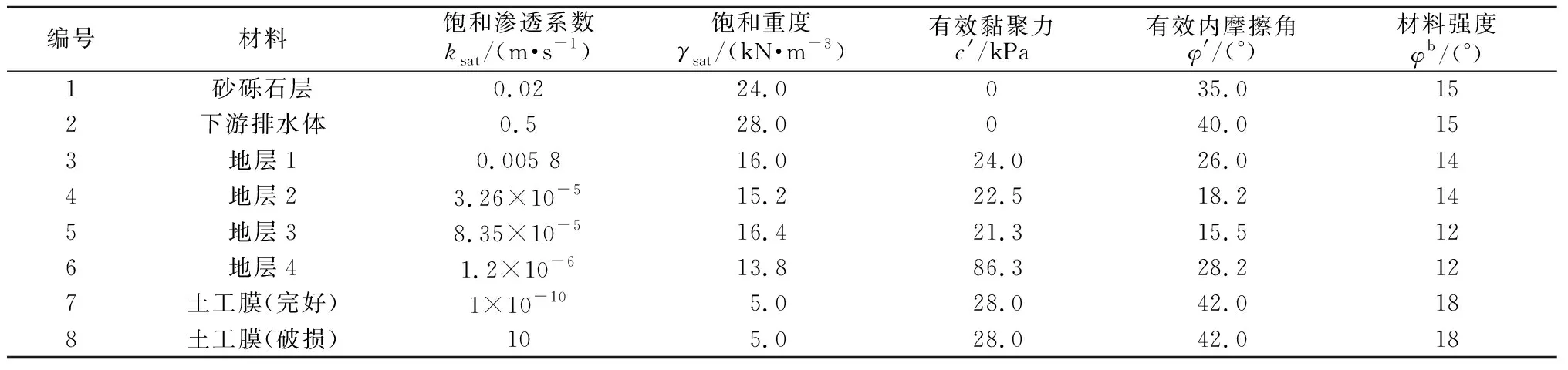
图2 土体渗透系数曲线及土-水特征曲线Fig.2 Permeability coefficient curves and soil-water characteristic curves

3.3 库水位骤降下土工膜缺陷模拟工况

由于土工膜缺陷发生位置的随机性[10]，本文分别取上部(18.0 m高程)、中部(12.0 m高程)、底部(6.0 m高程)3种方案，并结合不同库水位下降速率(2.00，1.00，0.50，0.25 m/d，由正常蓄水位22.0 m高程下降至死水位5.0 m)进行，土工膜破损的尺寸大小分别取孔径为0.1 m和0.2 m的圆形缺陷，具体工况如表2所示。

表2 计算工况Table 2 Calculation conditions

3.4 模型范围及初始、边界条件

模型范围：如图1所示，模型取b点为坐标原点，水平方向为x轴，垂直方向为y轴，模型底部取至-55.0 m高程，左右各延伸50 m。采用三角形和四边形单元，整个模型共划分了1 210个节点，1 154个单元。在土工膜处网格作了细化，整体模型如图3所示。

图3整体模型
Fig.3Diagramoftheglobalmodel

初始条件：各种工况均取不同土工膜缺陷部位以及不同尺寸的情况的稳态分析结果作为各个工况瞬态分析的初始条件。

边界条件：如图1所示，bcdef为上游变水头边界，以模拟不同工况中库水位下降速率的不同。Geo-slope软件的Seep/W模块提供了这种边界条件的处理方法[9]：设定水库上游坡面水头为随时间变化的函数，对于某一时刻，当节点上的水头小于该节点的高程，则节点上的边界流量Q=0。kl为下游0水头边界，ba，am，ml，fgh为不透水边界，hijk为自由渗出边界。

4 成果分析

4.1 土工膜缺陷渗流场分析

土工膜缺陷不同部位稳定渗流下的浸润线位置如图4所示。由图4可知，浸润线高程变化幅度较大的部位为面膜坝的上游坝坡，因此，在上游库水位骤降的情况下，作用在上游坝坡上的水压力的卸载容易导致上游坝坡失稳。

图4不同缺陷部位的稳态浸润线位置
Fig.4Positionofsteady-statephreationlinesatdifferentpositionsofdefects

表3列出了不同工况稳定渗流场下渗漏量与膜厚浸润线的数值。

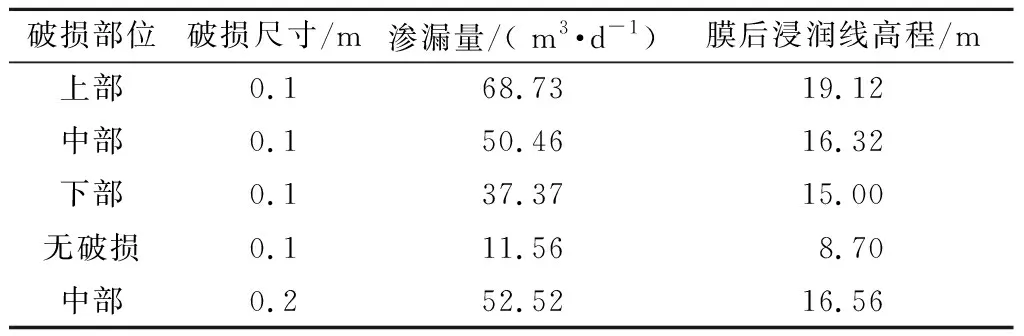
表3 不同工况稳定渗流渗漏量与膜厚浸润线Table 3 Stable seepage results in different working conditions

由表3可见，在土工膜无破损情况下，渗漏量与膜后浸润线高程最低，一旦发生破损(如表3中工况下部破损所示)，渗漏量和膜后浸润线高程分别增加了223.27%和72.41%，可见一旦发生土工膜失效，对面膜坝渗流要素的影响十分巨大。在破损尺寸相同时，土工膜缺陷位置越高，坝内浸润线的位置也越高，浸润线坡度也较陡，对坝体稳定较为不利；土工膜破损尺寸越大，浸润线高程越高，但是影响程度没有缺陷位置的影响程度大。通过坝体的渗漏量也随着土工膜缺陷的上移而变大，最大渗漏量发生在土工膜上部破损时，为68.73 m3/d，最小渗漏量为土工膜无破损时，为11.56 m3/d，土工膜破损尺寸对渗漏量也有一定的影响，尺寸越大，渗漏量也越大，但是影响并不是很大。总体来说，土工膜破损位置对面膜坝的渗漏量和浸润线高程的影响较破损尺寸要大。

坝内浸润线随着库水位的下降而降落,当库水位通过土工膜的破损部位时，坝内浸润线有一个“突变”。这是由于破损部位至以下高程的土工膜又形成了一个完整的防渗体系，使得坝内的浸润线突然降低，这里以工况B-4的膜后浸润线高程变化为例，如图5所示：第39天由于库水位高程高于土工膜缺陷高程，存在土工膜缺陷的渗漏通道，使得坝内浸润线较高；第40天由于库水位降至土工膜缺陷高程以下，库水位高程以下不再存在渗漏通道，坝内浸润线便产生了“突变”的效应。

图5工况B-4膜后浸润线变化
Fig.5ChangeofphreaticlineinworkingconditionB-4

4.2 上游坝坡稳定性分析

不同工况的计算时间长度统一取为80 d，安全系数随时间变化如图6所示。

可以看出，随着库水位的下降，上游坝坡安全系数先下降，最终趋于一个稳定值，并且库水位下降的速率越快，安全系数下降越剧烈。初始条件的不同，使得不同工况的安全系数分布也不一样，土工膜无破损时(工况D)初始安全系数最高，为2.347，随着土工膜破损位置逐渐上移，初始安全系数逐渐变小，并且土工膜破损尺寸越大，安全系数也越小。在库水位高程降落至土工膜破损高程时，安全系数有一个陡然上升的“突变”，究其原因为坝内浸润线突然下降，导致上游坝坡的安全系数变大的缘故。土工膜破损位置对安全系数“突变”的幅度也有一定的影响，破损位置高程越低，“突变”的幅度也就越小，并且破损尺寸越大，“突变”幅度也就越小。

图6不同工况安全系数随时间的变化曲线
Fig.6Safetyfactorversustimeindifferentworkingconditions

5 结 论

本文针对于深厚覆盖层上某面膜坝，利用Geo-slope软件对不同位置(上部、中部、下部)、不同尺寸(0.1 m和0.2 m)的土工膜缺陷进行了数值模拟，考虑了不同库水位下降速率工况(2，1，0.5，0.25 m/d)的影响，得出了以下结论：

(1)土工膜缺陷的位置和尺寸是影响面膜坝渗流场的重要因素。面膜坝内初始浸润线高程与渗漏量随着土工膜破损位置的上升、缺陷尺寸的变大而增大，但后者影响明显小于前者。

(2)库水位下降过程中坝体内部浸润线下降滞后于库水位，当库水位降落至土工膜破损高程以下时，坝体内部浸润线下降存在一个“突变”。

(3)面膜坝安全系数总体变化趋势是先下降，再趋于稳定，库水位下降速率越快，安全系数变化越剧烈，当库水位降落至土工膜破损高程以下时，安全系数存在一个陡然上升的“突变”。

(4)本文只考虑了土工膜破损位置与尺寸大小对于面膜坝渗流特性以及稳定性的影响，对于其他影响因素例如土工膜与其下垫层的接触情况对于面膜坝上游坝坡稳定性的影响有待进一步的研究。