K0应力条件下砂土小应变剪切模量研究

，，2，

(1.同济大学 a.地下建筑与工程系；b.岩土与地下工程教育部重点实验室，上海 200092；2.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221008 )

1 研究背景

Atkinson等[1]将土体应变范围划分为非常小应变(<0.001%)、小应变(0.001%～1%)、大应变(>1%)3个区域。在非常小应变情况下，剪切模量基本不变，此时的剪切模量通常称为小应变剪切模量或最大剪切模量G0。小应变剪切模量G0以及小应变范围内土体剪切模量的变化规律对描述土体小应变特性十分关键[2]。目前在实验室内测试土体G0的方法主要有共振柱[3-7]和弯曲元试验[8-9]等。由于弯曲元测试剪切波速的原理明确、方法简单直观，目前在三轴仪、固结仪、直剪仪和共振柱等室内仪器上已被广泛应用[10]。在弯曲元测试中，剪切波引起的土体应变量级在10-5以内，因此土体剪切波速与小应变剪切模量可通过弹性理论计算得到，即

(1)

式中：ρ是土体的密度；Vs是土体的剪切波速；L是剪切波传播长度；t是剪切波传播时间。

以往对砂土的小应变剪切模量G0进行了大量的研究，结果表明有效围压、孔隙比等对G0有重要的影响。目前研究主要集中在制样方法或砂土微观组构、颗粒形状特性、各向异性等对G0的影响。例如，Rashidian等[11]研究了潮湿夯实法(MT)、水中沉降法(WS)和空中砂雨法(AP)等制样方法对丰浦砂剪切波速的影响； Alba等[12]、Gu等[13]通过研究表明MT法制备的试样的G0比AP法的G0大20%左右；Murphy[14]和刘瑜、夏唐代[15]通过对3种不同的砂样进行研究，得出砂粒的颗粒粗糙度对剪切波速的影响显著，剪切波速随着颗粒粗糙度的增加而减小；李博等[16]研究了K0固结条件下砂土的沉积角度对G0的影响，结果表明沉积角度为90°的砂样的G0最大。但遗憾的是，李博等的研究中无法测定砂土的应力状态这个重要的影响因素。值得注意的是，天然砂土处于K0应力状态，因此非常有必要研究不同密实度条件下砂土的侧向土压力系数K0，以及真实K0应力状态下的小应变剪切模量。

2 试验概况

2.1 试验材料和仪器

本次试验采用丰浦砂，该砂粒的相对密度Gs为2.65，平均粒径D50为0.18 mm, 级配曲线的不均匀系数Cu为1.62，其最大孔隙比emax为0.931，最小孔隙比emin为0.611。试验采用英国GDS应力路径三轴仪，能够实现围压、孔压和轴压的单独控制，对试验过程中土体的进出水量、位移和应力变化能够精确测量。通过改装配置一对压电陶瓷弯曲元，能进行土样剪切波测试。弯曲元宽11 mm，厚1.2 mm，插入土样的深度为2 mm，如图1所示。弯曲元测试剪切波速的具体原理可以参照文献[6]—文献[9]。

图1弯曲元示意图
Fig.1Benderelement

2.2 试验方法

此次试验砂样的尺寸为直径50 mm，高度100 mm。试验分为4组，每组试验砂样的相对密实度分别为90%，70%，55%，45%。制样采用干砂压实法，为保证砂样的均匀性，分5层击实。采用CO2充气和反压饱和，饱和过程设定围压目标值为210 kPa，反压目标值为200 kPa。为保证试样顶帽与轴力杆的有效接触，设置偏应力为2 kPa。饱和结束后，测得每个试样的孔隙水压力系数B值为0.99左右，试样处于完全饱和状态。然后进行K0固结，K0固结过程中设定有效围压目标值为200 kPa。固结结束后，通过式(2)计算得到K0值。在K0固结过程中，测试在有效围压分别为10，30，60，100，150，200 kPa下的剪切波速，并计算该状态下的小应变剪切模量G0。

(2)

3 试验结果分析

3.1 相对密实度Dr和K0的关系

以相对密实度为90%的试样为例，在K0固结过程中，试样的轴压、围压和孔压随时间的变化关系如图2(a)所示，试样的轴向变形、体积变形和侧向变形随时间的变化如图2(b)所示。试验过程中轴向变形通过三轴仪内置的轴向LVDT测量得出，体积变形则通过反压控制器的体积变化求出。由于土体饱和，侧向变形则可通过体积变形和轴向变形反算得到。

由图2(a)可见，轴压和围压在刚开始固结时有轻微的不稳定，3 000 s后轴压和围压稳定以线性增长。由图2(b)可知，K0固结过程中侧向应变维持在0%附近，侧向应变符合K0固结变化规律。轴向应变和体积应变变化规律一致，符合K0固结的前提条件。固结结束后，4组试样的K0值如表1所示。

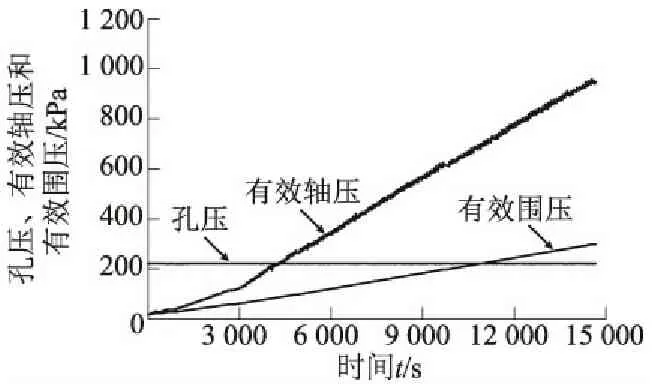
(a)有效轴压、有效围压和孔压

(b)轴向、侧向和体积应变

图3 相对密实度随K0值变化 Fig.3 Relative density of sand vs.K0 value

图3进一步给出了试样的K0值和相对密实度的关系。通过表1和图3可以很明显地看出，随着密实度的增加，砂土的K0逐渐减小，并且密实度越大，K0减小得越快。

3.2 砂土的小应变剪切模量

为了更好地测定剪切波在土样中的传播时间，试验采用了5种不同的激发频率，分别为2，5，10，20，50 kHz。由于方形波的近场效应很明显，难以确定波的到达时间，因此此次试验发射波采用的是正弦波。图4是相对密实度为70%的砂样在K0固结后不同频率下的剪切波(S波)波形图。判断剪切波通过土体的时间t是弯曲元试验中一个关键的问题。常用的方法包括初达波法(start-to-start)、峰值法(peak-to-peak)和多次发射法(multiple- reflection)。初达波法直观明了，结果相对可靠，文献中也大都采用该方法[11,13]。本文也采用初达波法对剪切波信号进行分析和讨论。

图4Dr=70%时K0固结结束后的剪切波信号
Fig.4WavesignalsunderK0consolidationwhen
Drequals70%

在发射S波时，会同时产生压缩波(P波)，而P波的速度更快，因此更早被接收弯曲元接收，特别是在饱和土体中[11,17]。因此，接收信号的前部为P波，且频率很高，特别是在输入频率较高时，P波对S波的干扰更加明显。同时，弯曲元测试中，还存在一定的近场效应，该近场效应与S波的极化方向相反，且随着频率的增加幅值减小。因此，P波和近场效应会对S波造成一些干扰，导致S波传播时间难以准确确定。

综合以上分析并考虑不同频率下的波形特点，采用初达波法基于5 kHz时的波形图确定S波的传播时间为290 μs(图4)。同时，根据LVDT轴向位移量测和GDS控制器体积应变量测，确定试样在不同应力下的试验高度和孔隙比，并计算剪切波的传播距离和试样密度，从而算出G0。剪切波的传播距离为弯曲元传感器顶端间的距离。表2给出了不同应力状态下土体的小应变剪切模量G0。

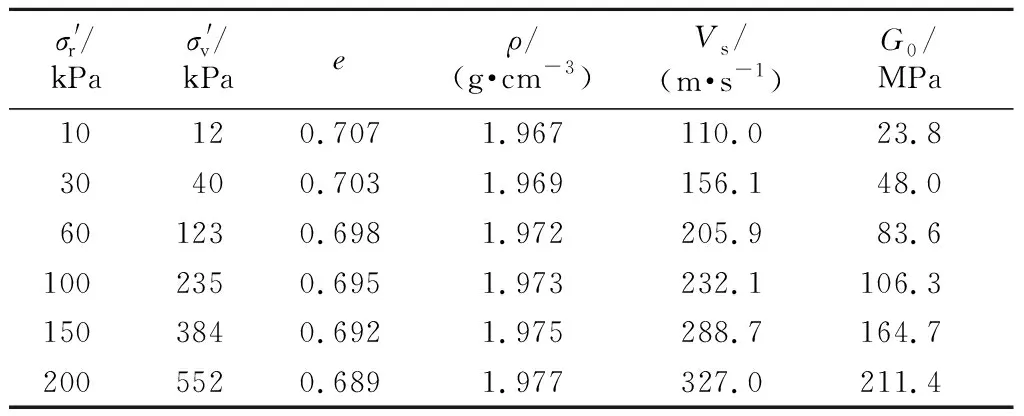
表2 70%密实度试样在K0固结过程中的相关参数Table 2 Parameters under K0 consolidation whenDr equals 70%

对4组不同密实度下砂土K0固结后的剪切波速进行测试，计算出对应的小应变剪切模量G0，如表3所示。

表3 4组试验砂土固结后的相关参数Table 3 Parameters of sand after consolidation

图5 G0随孔隙比e 的变化情况 Fig.5 Curve of G0 vs. porosity e

将初始孔隙比e和小应变剪切模量G0的关系绘制在折线图上，如图5所示。从表3和图5可以看出，在相同K0固结条件下，随着孔隙比的增大，小应变剪切模量减小。

砂土的G0通常可由式(3)预测[18]，即

(3)

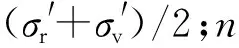
(4)

图6给出了4组试样G0/F(e)和σ′的关系。由图6可见，土体的小应变剪切模量G0随着平均有效主应力的增加而增加，且4组试样存在比较统一的关系，表明预测公式较好地反映了平均主应力和孔隙比对G0的影响。经拟合得知A=70.15，n=0.67。

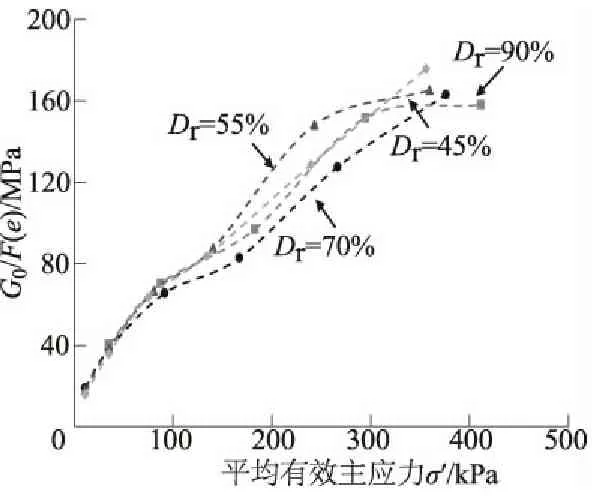
图6G0/F(e)随平均有效主应力σ′的变化情况
Fig.6CurvesofG0/F(e)vs.σ′

3.3 砂土K0系数和G0的关系

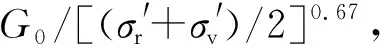
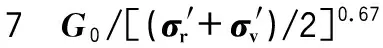
4 结 论

本文通过应力路径三轴仪研究了不同密实度砂土的侧向静止土压力系数K0以及K0应力条件下砂土的小应变剪切刚度G0，并初步尝试建立了砂土K0和G0的关系，结论初步如下。

(1)对4组不同密实度的丰浦砂开展K0固结试验，在K0固结过程中，体积应变和轴向应变变化规律保持一致，应变大小也很接近，证明侧向变形几乎为0，符合K0固结的变化规律。试验结果表明随着密实度的增加，孔隙比的减小，静止土压力系数K0逐渐变小，并且孔隙比越小，K0系数变小得越快，K0系数和密实度呈现较好的相关性。

(2)丰浦砂的小应变剪切模量G0在K0固结应力状态下随密实度的增加而增加，同时G0/F(e)随平均主应力的增大而增大，且4组试样存在较为统一的规律。其规律可通过应力函数和孔隙比函数很好地反映，通过拟合得出参数A和n的值分别为70.15和0.67。该公式对求解K0固结状态下不同密实度、不同应力状态下的小应变剪切模量有较好的参考意义。