颗粒破碎对钙质砂压缩特性影响的试验研究*

李彦彬 李 飒 刘小龙 陈文炜

(①天津大学建工学院岩土所， 天津 300072， 中国) (②中国船舶重工集团公司第702研究所， 无锡 214082， 中国)

0 引 言

钙质砂作为一种含碳酸钙及其他碳酸盐类物质成分达50%以上的海洋沉积物，在我国南海海域分布广泛(陈海洋等， 2005)。作为在南海岛礁建设中常用的工程基础填料，对其工程力学性质的研究十分重要。钙质砂的土颗粒具有形状不规则、富含孔隙、棱角度高及易破碎等特点，其中易破碎性是影响钙质砂工程特性的重要因素，导致其与一般陆相沉积物的工程力学性质有很大差异(白晓宇， 2010； 袁征等， 2016)。

近年来，国内外众多学者基于三轴试验、剪切试验、侧限压缩试验和冲击荷载试验等对钙质砂的基本力学特性和颗粒破碎特性进行了大量研究(沈建华等， 2010)。研究表明，钙质砂是一种极易破碎的粗颗粒土，在常压条件下即会产生颗粒破碎，且颗粒破碎对其变形和强度将会产生重要影响(吴京平等， 1997)。

Fawad et al.(2003)在侧限压缩试验中研究发现黏粒含量、不均匀系数、中值粒径等参数都是影响砂土压缩变形量的重要因素。刘崇权等(1998)，张家铭等(2005)通过侧限压缩试验研究发现钙质砂的压缩特性与黏土类似，但是其卸载回弹比黏土小很多，且由于钙质砂极易破碎的特性，导致其压缩性质不同于一般陆源砂。毛炎炎等(2017)通过对不同含水率条件下的钙质砂进行侧限压缩试验研究，发现粒径、含水率对颗粒破碎和压缩变形产生影响，得到了含水率与相对破碎率和压缩指数之间的关系曲线。马启锋等(2018)通过侧限压缩试验对钙质砂和石英砂研究发现，在高应力作用下，钙质砂比石英砂的压缩变形量大，钙质砂的屈服应力远远低于石英砂。乐天呈等(2018)研究发现不同级配和颗粒形态对于砂土压缩特性具有一定影响。李飒等(2019)研究表明碳酸钙含量是影响砂土的破碎特性与强度特性的重要因素之一。

对于颗粒破碎性质，也有许多学者做出了研究。吴京平等(1997)通过三轴等向固结试验研究发现，钙质砂的破碎程度与试样在受力过程中所吸收的塑性功大小密切相关，且建立了相对破碎率Br与塑性功Wp之间的关系式。Nakata et al.(2001)和梁军等(2003)发现在侧限压缩试验中石英砂和钙质砂的屈服应力都与单颗粒破碎强度有关。朱晟等(2018)研究发现堆石料的颗粒破碎和变形特性与其物理力学性质和级配密切相关。钙质砂在压缩过程中，其级配必定也是影响颗粒破碎的重要因素。陈火东等(2018)通过试验研究了不同相对密度和围压下的颗粒破碎规律，分析得出颗粒破碎对钙质砂应力-应变曲线影响。

颗粒破碎是一个在颗粒级配、颗粒形状、密实度和矿物含量等多种因素影响下的复杂过程，对钙质砂的压缩特性影响很大，值得深入研究。本文对4种钙质砂样进行侧限压缩试验，分析相对密实度Dr、中值粒径d50和碳酸钙含量对钙质砂颗粒破碎与压缩变形的影响，通过考察塑性功与相对破碎率、以及塑性功和压缩指数之间的关系，探讨了钙质砂颗粒破碎与压缩特性之间的规律。

1 试验方法及结果

试验所用钙质砂分别取自中国南海海域与阿拉伯湾海域。图 1为两种钙质砂放大100倍后的电镜扫描照片。可以看出，两者的颗粒形状有着明显差异，且颗粒棱角度不同。其中，南海钙质砂颗粒形状不规则，颗粒表面富有孔隙、凹凸不平，而阿拉伯湾钙质砂表面较为光滑，在相同的放大倍数下未见明显孔隙。

图 1 钙质砂扫描电镜图(100倍)Fig. 1 SEM of calcareous sands(100x)a. 南海钙质砂； b. 阿拉伯湾钙质砂

本次试验所配制的钙质砂包含砂样1、砂样2、砂样3、砂样4 4种砂样。砂样1， 砂样2为取自南海岛礁的现场天然级配的土体。其中砂样1的d50=0.40imm，黏粒含量较少，占总体土样的1.09%； 砂样2的d50=0.15imm，黏粒含量较多，占总体土样的18.4%，两者d50相差较大。砂样3利用南海钙质砂，采用与阿拉伯湾钙质砂相同的级配制成，而砂样4为取自阿拉伯湾的钙质砂，即砂样3与砂样4级配完全一致。各砂样的基本物理参数和级配如表 1和图 2所示。

由表 1所示数据可见，虽然砂样3和砂样4具有相同的级配，但是其最大、最小干密度存在较大差异。结合图 1可以看出，除级配外，颗粒形状对钙质砂的密度也有影响。

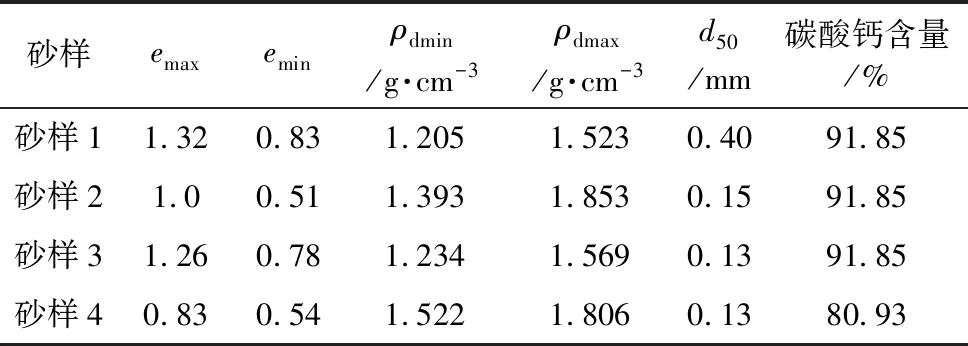
表 1 各砂样基本物理参数Table 1 Basic physical parameters of sample

图 2 各砂样颗粒级配曲线Fig. 2 Particle size distribution of samples

根据《土工试验规程(SL237-006-1999)》进行侧限压缩-回弹-再压缩试验，将4种钙质砂的初始相对密实度分别控制为0.3、0.6和0.8，从12.5ikPa加载至3200ikPa后按加载路径依次卸荷至25ikPa，并重新加载至4000ikPa。为了评价试验过程中的颗粒破碎情况，在每组试验前后对各试样进行颗粒筛分，比较试验前后粒径分布的差异，以探究钙质砂在侧限压缩下的颗粒破碎规律。由于本次试验主要探讨颗粒破碎对钙质砂压缩特性的影响，整个试验过程中，采用完全干燥试样。在这种试验条件下，土体的压缩性只与加载初始阶段发生的颗粒重排、颗粒破碎以及颗粒破碎后导致的重新排列有关。在此，将颗粒破碎以及颗粒破碎后导致的重新排列均视为颗粒破碎导致的压缩变形。

图 3 砂样1， 砂样2压缩-回弹-再压缩曲线Fig. 3 Compression-rebound-recompression curves of sand samples 1， 2a. 砂样1； b. 砂样2

图 4 砂样3， 砂样4压缩-回弹-再压缩曲线Fig. 4 Compression-rebound-recompression curves of sand samples 3， 4a. 砂样3； b. 砂样4

经计算得各砂样回弹指数Ce均在0.0020～0.0056之间，说明钙质砂的压缩变形以不可恢复的塑性变形为主。

2 试验结果分析

2.1 颗粒破碎特性

以相对密实度Dr=0.3为例，给出4种砂样压缩前后的颗粒分布曲线(图 5、图 6)。其表明各砂样在压缩前后，粒径分布均发生了变化，颗粒产生破碎。且砂样1和砂样3的变化情况分别大于砂样2和砂样4。在定量分析颗粒破碎对钙质砂压缩特性的影响时，需要确定颗粒破碎的情况。Hardin定义的相对破碎率如下：

Br=Bt/Bp0

图 5 砂样1， 砂样2压前压后颗分曲线(Dr=0.3)Fig. 5 Fractional curves of sand samples 1， 2 before and after the tests(Dr=0.3)

图 6 砂样3， 砂样4压前压后颗分曲线(Dr=0.3)Fig. 6 Fractional curves of sand samples 3， 4 before and after the tests(Dr=0.3)

式中，Bp0为破碎势能，是受压前的颗分曲线与粒径d=0.074imm竖线所围面积；Bt为总破碎量，是受力破碎后的颗分曲线与受力前曲线和d=0.074imm竖线围成的面积。

根据筛分前后颗粒级配曲线整体变化情况，分别计算4种砂样的Br，得出Br随Dr变化的曲线图(图 7)。由图可得，砂样1， 砂样2， 砂样3的Br随着Dr的增加而增加； 而对于砂样4，Br在不同的Dr下基本保持不变。

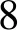
图 7 相对密实度Dr与相对破碎率Br的关系Fig. 7 Relationship between Dr and Br

图 8 中值粒径d50 与相对破碎率Br的关系Fig. 8 Relationship between d50 and Br

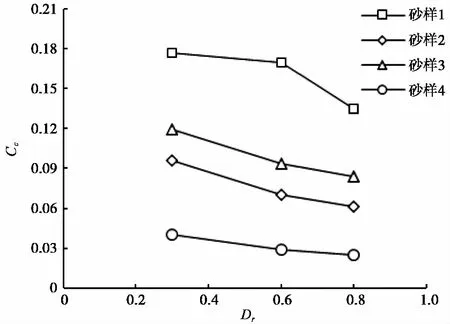
图 9 相对密实度Dr与压缩指数Cc的关系Fig. 9 Relationship between Dr and Cc

2.2 压缩特性

在本次试验中，钙质砂的碳酸钙含量对于Cc和Br的影响均表现出了正相关的特征。

图 10、图11为侧限压缩模量Es随上覆压力p的变化图。从图 10中可见，对于砂样1， 砂样2，Es-p曲线较为光滑，没有出现明显的屈服点，这与Fawad et al.(2003)研究成果一致，说明在较小的应力条件下，钙质砂颗粒已经发生了破碎。在相同的密实度条件下，砂样1的Es低于砂样2。由图 11可得，砂样4的Es-p曲线全部位于砂样3之上，说明砂样4的Es明显高于砂样3。同时砂样4曲线出现了较明显的屈服点，其曲线趋势与石英砂的曲线趋势相近。由此可见碳酸钙含量对于土体的破碎压缩有着明显的影响。

图 10 砂样1， 砂样2的Es-p曲线Fig. 10 Es-p curves of sand samples 1， 2

图 11 砂样3， 砂样4的Es-p曲线Fig. 11 Es-p curves of sand samples 3， 4

3 颗粒破碎对压缩特性的影响

为了探讨颗粒破碎对钙质砂压缩特性的影响，采用塑性功的概念进行分析(杨光等， 2010)。定义上覆压力对砂样单位体积输入的塑性功为产生塑性体应变与弹性体应变时所消耗的能量之差，即：

dWp=pdεv-pdεve

(1)

由于钙质砂在侧限压缩试验过程中发生的塑性变形占总变形的绝大部分，弹性变形很小，因此产生弹性变形所消耗的能量可以忽略不计。即可采用正应力与体积应变的积分计算塑性功，如式(2)所示：

(2)

根据试验结果，绘制塑性功Wp随Dr变化的曲线图(图 12)。可见，砂样越密实，土体输入的Wp越小。结合图 9可以看到，Wp随Dr变化的规律与Cc类似。

图 12 塑性功Wp与相对密实度Dr的关系Fig. 12 Relationship between Wp and Dr

图 13 塑性功Wp与相对破碎率Br的关系Fig. 13 Relationship between Wp and Bra. 不同相对密实度下Br-Wp关系； b. Br-Wp归一化拟合结果

钙质砂的颗粒破碎程度与其在受力过程中所吸收的Wp大小有着密切联系。对Wp与Br关系的研究中发现两者呈现双曲线或者幂函数关系(刘汉龙， 2005； 王远， 2018)，本文采用幂函数对两者之间的关系进行探究：

Br=a(Wp)b

(3)

式中，a，b与钙质砂的基本物理性质等因素有关。按照式(3)，将实验数据计算得出的Br与Wp进行拟合，结果如图 13所示。由图 13a可以看到，在一定压力范围内，不同Dr的Wp与Br之间存在不同的相关性，且都可用幂函数拟合。

根据图 7和图 12中Br，Wp与Dr的关系，利用Dr对Br和Wp进行归一化后拟合结果如图 13b所示，得到式(4)：

Br/Dr=a′(Wp/Dr)b′

(4)

其中，a′=0.0012，b′=0.73。

如前所述，Wp随Dr变化的规律与Cc类似，因此建立了Wp与Cc之间的关系图(图 14)。可见在本次试验条件下，两者呈现良好的线性关系，Cc随Wp的增加而增加。

图 14 Wp与Cc之间的关系图Fig. 14 Relationship between Wp and Cc

所以，由Wp与Br间存在幂函数关系可进一步探讨Cc与Br之间也存在幂函数关系：

Cc=A(Br)B

(5)

拟合结果如图 15所示。由图 15a可以看到，对不同的Dr，存在不同的参数A、B使得Cc与Br呈幂函数变化。同样利用Dr对Br和Cc进行归一化后，拟合结果如图 15b所示，拟合效果良好，从而可得式(6)：

Cc/Dr=A′(Br/Dr)B′

(6)

其中，A′=8.50，B′=1.41。

图 15 相对破碎率Br与压缩指数Cc的关系Fig. 15 Relationship between Br and Cca. 不同相对密实度下Cc-Br关系； b. Cc-Br归一化拟合结果

式(7)建立了一个可以将Dr纳入考虑因素的Cc-Br数学关系模型，该模型可以在一定范围内评价钙质砂颗粒破碎对其压缩特性的影响。

4 结 论

通过对不同初始相对密实度的4种钙质砂样进行侧限压缩试验，分析了中值粒径d50和碳酸钙含量对压缩变形与颗粒破碎特性的影响，建立了塑性功Wp与相对破碎率Br、压缩指数Cc与相对破碎率Br之间的关系，得到如下主要结论：

(1)在本试验条件下，钙质砂压缩-回弹-再压缩曲线中，回弹曲线几乎水平，回弹指数在0.0020～0.0056之间，颗粒破碎引起的不可逆的塑性变形是构成钙质砂压缩变形的主要部分。

(2)中值粒径d50以及碳酸钙含量对钙质砂的破碎特性具有重要影响，进而对土体的压缩特性产生影响。中值粒径d50越大，碳酸钙含量越高颗粒破碎越显著，土体的压缩性也越大。

(3)钙质砂的相对破碎率Br随着塑性功Wp的增大而增大，且与土体的初始相对密实度Dr有关，采用Dr进行归一化后，相对破碎率Br与塑性功Wp呈现良好的幂函数关系。

(4)在本次试验条件下，钙质砂的塑性功Wp与压缩指数Cc呈现良好的线性关系。因此可以建立相对破碎率Br与压缩指数Cc的关系，采用Dr进行归一化后，相对破碎率Br与压缩指数Cc同样呈现良好的幂函数关系。