基于强度折减法的土石混合体边坡长期稳定性研究*

刘康琦 刘红岩 祁小博

(①中国地质大学(北京)工程技术学院， 北京 100083， 中国) (②自然资源部深部地质钻探技术重点实验室， 北京 100083， 中国) (③中国地质环境监测院， 北京 100081， 中国)

0 引 言

土石混合体边坡是第四纪以来形成的、由土和块石组成的一种极度不均匀的岩土体边坡。不同于一般的土质边坡或岩质边坡，由于块石与土的共同存在，使土石混合体边坡具有极大的不均匀性和不连续性。目前针对土石混合体边坡的稳定性已有较多研究，油新华等(2002)通过对土石混合体进行野外水平推剪试验，得出土石混合体的变形特点和相关的抗剪强度参数，并发现土石混合体在剪切破坏时会绕过大的石块。徐文杰等(2009)将土石混合体定义为第四纪以来形成的，由具有一定工程尺度、强度较高的块石、细粒土体及孔隙构成且具有一定含石量的极端不均匀松散岩土介质系统，并通过可视粒径、土石阈值、“土”与“石”的强度特征及含石量4个参数对土石混合体的概念进行了补充。Zhou et al.(2019)利用室内循环冻融试验和PFC3D数值模拟研究了冻融循环对土石混合体强度的影响。徐文杰(2009)基于对周家湾滑坡的大量地质调查研究，对土石混合体滑坡体进行了工程地质分区，并建立了三维地质模型，运用有限元强度折减法分析了其稳定性。杨忠平等(2017)基于PFC2D接触黏结模型的离散元数值模型，研究了含石量变化对土石混合体剪切特性的影响。龚健等(2017)通过对不同含石量的土石混合体进行静力超载试验，得出土石混合体的力学行为与含石量的关系，另基于PIV分析方法，研究了剪切破坏时剪切带的发展规律。张森等(2016)提出基于颗粒流区域填充技术的土石混合体有限元随机生成技术，并利用强度折减法研究了含石量对边坡稳定性的影响规律。Sun et al.(2014)通过对冷谷水电站马河堆积体进行工程类比、颗粒分析试验、直剪试验、现场大型推剪试验、数值模拟试验、参数反演等研究，对比分析了土石混合体的抗剪强度，并对马河堆积体的稳定性进行了分析。Fan et al.(2015)使用离散元数值模拟方法，研究了土石混合体在循环荷载作用下的力学特性，结果表明峰值应力会随着动应力幅值和频率的增大而增大，但会随着块石所占比例的增大而减小，同时弹性模量会随着动应力幅值和频率的增大而减小。郑博宁等(2019)提出了基于CT扫描技术和PFC三维颗粒流程序的土石混合体三维建模技术，并通过与三轴剪切试验过程中砾石的空间运动规律进行对比分析，验证了其建模方法的可行性。Wang et al.(2019)利用离心模型试验通过考虑不同体积块石含量，研究了土石混合体边坡在地表荷载作用下的破坏行为。Lu et al.(2018)使用离散元法研究了含石量、坡高比和块石大小对土石混合体边坡稳定性的影响。Yang et al.(2019)利用修正数值流形法研究了连续开挖条件下土石混合体边坡的稳定性。

然而目前对土石混合体边坡稳定性的研究，基本都忽略了土体的蠕变效应。研究表明(陈卫兵等， 2008； 蒋海飞等， 2013； 陈廷君等， 2019)，土体蠕变会降低坡体的稳定性系数，对边坡稳定性造成不利影响。本文首先利用数字图像处理技术对我国某水电站库区的一个土石混合体边坡进行处理，最大化的获得土石混合体边坡的细观模型，然后利用FLAC3D程序中强度折减法对其进行稳定性分析，并考虑了土体的蠕变性质，对比分析了考虑土体蠕变的土石混合体边坡与不考虑土体蠕变的土石混合体边坡的变形特征。然后通过对采用不同土体蠕变参数的土石混合体边坡进行稳定性分析，讨论了土体蠕变参数对土石混合体边坡稳定性的影响。

1 土石混合体边坡模型的建立

1.1 数字图像处理

数字图像处理(Digital Image Processing)被最早用来改善图像的质量，而随着计算机科学的不断发展，其开始广泛应用于航空航天、医学、军事、工程等领域。近年来，数字图像处理技术也越来越多地被应用到岩土工程界(Chen et al.， 2004； Xu et al.， 2008; 徐文杰等， 2008； 廖秋林等， 2010； 王学滨， 2018)，它将图像经过数学变换后转换为数字信号并利用计算机对其进行分析处理，可将图像定义为一个非零的和有限的二维函数f(x，y)，其中(x，y)表示空间或平面坐标，f表示图像在该点处的灰度值。在对土石混合体边坡进行处理时，可根据土与块石灰度值的不同，通过设定阈值，将土与石块分别开来，这样利于提取土石混合体边坡中土与块石的分布信息。

在进行图像处理时依托于OpenCV强大的图像处理功能及Python语言的简洁高效，OpenCV是由C++语言编写的一种计算机视觉库(Bradski， 2000)，具有轻量、高效且开源的优点，并提供了多种语言的接口。

图 1 实际的土石混合体边坡图像Fig. 1 Image of soil-rock mixture slope

图 1为我国某水电站库区的一个土石混合体边坡的断面图像。对其具体处理时过程如下：

(1)新建.py文件。与需要处理的土石混合体边坡图像放置在同一文件夹下。

(2)边坡图像二值化处理。依次对图像进行均值滤波器去噪处理→图像灰度化处理，将原来的RGB彩色图像转化为灰度图像→灰度图像高斯滤波器去噪处理，以消除灰度图内的高斯噪声→自适应阈值二值化处理，可在图像局部范围内自适应一个阈值对图像进行二值化处理，将图像上石块的灰度值设置为0，呈黑色，土体的灰度值设置为255，呈白色，使用自适应阈值二值化可最大化消除光照等因素对图像造成的影响→腐蚀算法去噪处理。

(3)细节调整。使用Photoshop软件对二值化后的边坡图像内不理想的区域进行手工处理，使二值化图像最大化接近真实土石分布情况。

(4)光滑及矢量化处理。由于生成的二值化图像内石块边界粗糙会对数值模拟造成困难甚至会使数值模拟失败，因此有必要对其进行边界光滑处理。另数字图像并不能直接用于数值模拟，因此需要对其进行矢量化处理，生成AutoCAD可接受的DXF文件。图 2即为对图 1进行矢量化处理后的结果，土石比约为14︰1，最大粒径为1.37im。

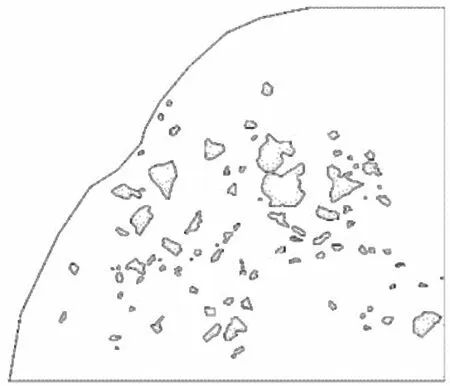
图 2 矢量化土石混合体边坡模型Fig. 2 Vector model of soil-rock mixture slope

1.2 建立模型

在进行数值计算时块石距离边坡边界过近会产生边界效应(徐文杰等， 2008)，为减少由于边界效应产生的影响，在边坡模型的右侧及左侧坡脚处使用均质土体进行了延拓，在AutoCAD中面域化后生成DXF文件导入ANSYS软件进行网格划分，然后转化为可供FLAC3D软件接受的文件格式。最终在FLAC3D中生成模型(图 3)，共生成节点10i906个，划分网格单元5455个，其中土体单元4736个，块石单元719个。

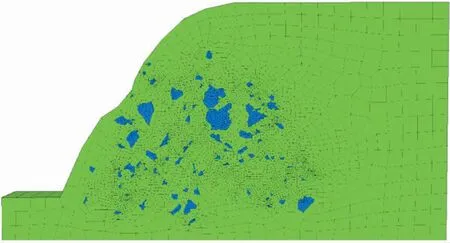
图 3 FLAC3D中生成的土石混合体边坡模型图Fig. 3 Model of soil-rock mixture slope in FLAC3D

2 考虑蠕变性质的强度折减法

2.1 强度折减法

由于传统的静力平衡法需要预先指定滑动面，不适于内部块石分布复杂的土石混合体边坡，因此采用强度折减法对边坡进行稳定性分析(Roth et al.， 1999)。强度折减法中将安全系数定义为边坡刚好达到临界失稳状态时，对岩土体的抗剪强度的折减程度。以莫尔-库仑强度屈服准则为例，采用强度折减法对边坡进行稳定性分析时，通过不断的对边坡的黏聚力c和内摩擦角φ除以折减系数进行试算，直到边坡达到失稳状态，此时的折减系数即是该边坡的安全系数，其折减过程如下：

(1)

(2)

式中，ctrial、φtrial为土体折减后的黏聚力、内摩擦角；Ftrial为折减系数；c、φ为岩土体折减前的黏聚力、内摩擦角。

2.2 蠕变本构模型的选取

在对蠕变边坡进行稳定性分析时，选取合适的黏弹塑性蠕变本构模型及参数可充分反映蠕变对边坡变形及稳定性的影响，直接关系到分析结果的合理性与正确性。一般来说，在选取蠕变模型时，应先进行室内试验，在试验数据的基础上利用蠕变理论选取合适的本构模型，然后利用回归分析和最小二乘法得出模型的参数。本文选取FLAC3D中Burgers黏弹性模型与Mohr-coulomb模型串联而成的Cvisc模型，其构成如下(图4)：

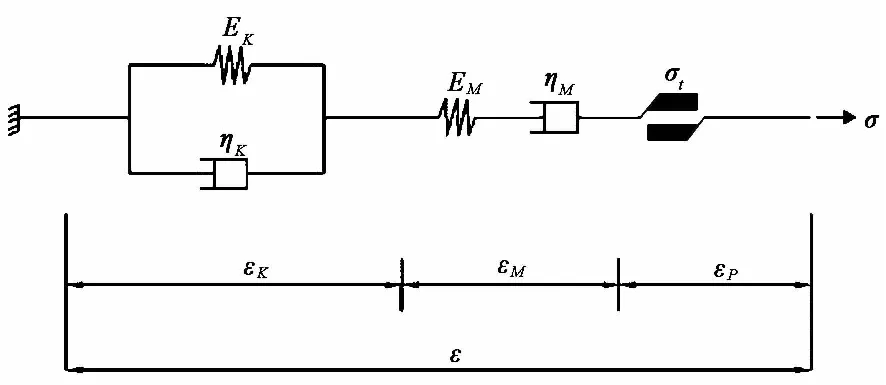
图 4 FLAC3D中Cvisc模型示意图Fig. 4 Illustrations of Cvisc rheological model in FLAC3D

在FLAC3D中，Cvisc模型由Kelvin体、Maxwell体和一个塑性体构成，其中，σ表示作用在岩土体上的应力；σt表示岩土体的屈服强度；EM、EK分别表示弹性模量和黏弹性模量；ηM、ηK分别表示Maxwell黏性参数和Kelvin黏性参数。在岩土体的蠕变变形中，若其具有稳定蠕变或加速蠕变性质，则即使不对岩土体的黏聚力和内摩擦角进行折减，边坡也会一直变形直至破坏，这样则无法体现边坡的变形失稳与岩土体强度之间的关系。因此需要将岩土体设定为只具有衰减蠕变性质，在FLAC3D中，只需将Maxwell黏性系数ηM设置为无限大即可，此时，Cvisc模型则退化为广义Kelvin黏弹塑性模型。

三维形式下模型应变增量偏量由Maxwell体、Kelvin体和塑性体3部分组成。分别为：

(3)

(4)

(5)

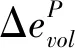
(6)

2.3 边坡失稳判据的选取

在使用强度折减法对边坡进行稳定性分析时，需要选取合适的失稳判据来判断边坡是否达到临界失稳状态。传统的强度折减法中，一般有3种方法用来作为判据：

(1)数值计算不收敛。当岩土体的强度参数折减到一定程度使边坡达到失稳破坏状态时，FLAC3D程序无法得到一个确定的解来满足静力平衡和应力-应变关系。

(2)关键点位移突变。可以通过监测若干关键点的位移来判定边坡是否破坏，当强度折减到一定程度使边坡达到临界破坏状态时，位移会突然增大。

(3)具有贯通的塑性区。当塑性区从坡顶一直贯通到坡脚时，可认为边坡已达到失稳状态。在FLAC3D中，可通过查看剪应变速率云图来观察塑性区是否贯通。

以上3种方法即为传统的强度折减法中边坡是否失稳的判据，而在考虑蠕变的土石混合体边坡稳定性分析中并不适用。一方面，由于块石的存在，很可能使边坡在破坏时不会出现明显贯通的塑性区； 另一方面，在考虑岩土体的蠕变性质时，很难以数值收敛作为边坡是否失稳破坏的判据。因此，可将关键点位移在经过一定时间后是否稳定及位移在强度折减到某个程度时是否突变作为土石混合体边坡是否失稳的判据(蒋海飞等， 2013)。

2.4 模型验证

为验证本文方法的正确性，使用自编蠕变强度折减法对陈卫兵等(2008)的算例进行对比。在对算例进行试算时，取土体参数如下：重度γ=20ikN·m-3，黏聚力c=35 kPa，内摩擦角φ=18°，剪胀角Ψ=18°，弹性模量和黏弹性模量分别为E=50 MPa、Ek=300 MPa，黏性系数ηk=5 GPa·d， 泊松比v=0.￣35，蠕变时间为1ia。通过不断折减土体强度参数，最后求得在考虑蠕变效应时该算例的安全系数为1.48，这与陈卫兵等(2008)的结果一致，因此可以认定本文所使用自编强度折减法是可靠的。图 5为该算例与使用自编强度折减法取折减系数为1.48时的剪应变速率云图。

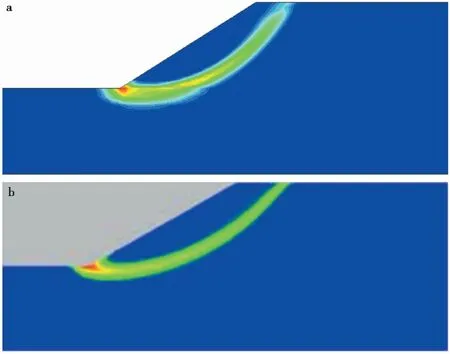
图 5 折减系数为1.48时剪应变速率云图Fig. 5 Contours of shear strain rate at reduction factor=1.48a. 本文计算结果； b. 文献计算结果(陈卫兵等，2008)

3 土石混合体边坡稳定性分析

计算模型的边界条件为：模型右侧及左侧边界采用水平约束，边坡底面采用水平、垂直全部约束。

3.1 考虑蠕变的土石混合体边坡稳定性分析

为作对比，首先研究不考虑蠕变效应时的土石混合体边坡稳定性，土体和块石均采用Mohr-Coulomb模型。基于蒋海飞等(2013)的研究，本文所选岩土体模型参数如表 1所示。

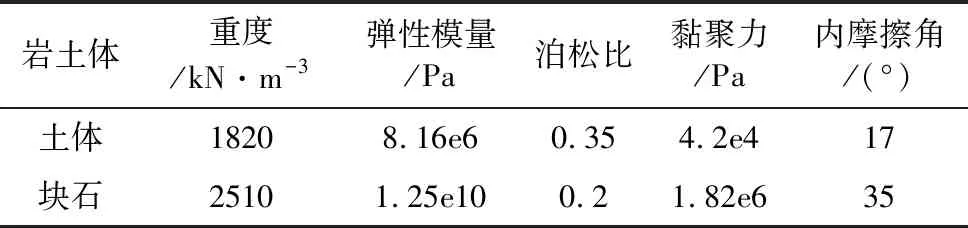
表 1 不考虑蠕变时模型参数表Table 1 Physico-mechanical parameters of S-RMS without considering rheology

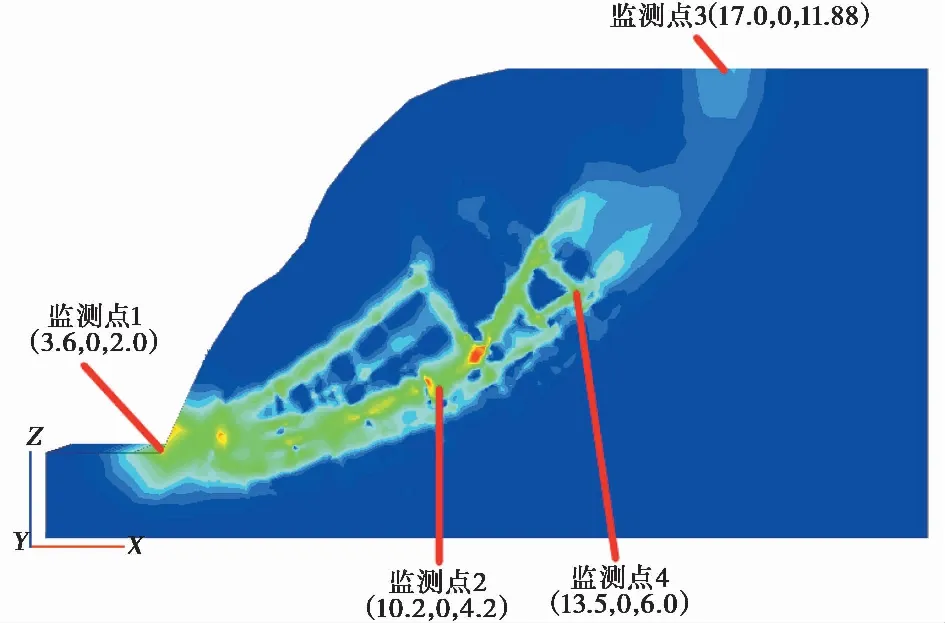
图 6 不考虑蠕变效应时边坡剪应变速率云图Fig. 6 Contours of shear strain rate without considering rheology

表 2 土体蠕变模型参数表Table 2 Physico-mechanical parameters of soil with considering rheology

图 6为不考虑蠕变效应时土石混合体边坡强度折减法的分析结果，可以看到，由于块石的存在，在边坡内部形成了多条滑带，而且滑带在靠近块石的部位有明显的“绕石”现象，由强度折减法得出的折减系数为1.85，即不考虑蠕变效应时此土石混合体边坡的安全系数为1.85。

在对考虑蠕变效应的土石混合体边坡进行稳定性分析时，在可能的滑带上及坡顶坡脚处选择关键点来监测其水平位移情况(陈卫兵等， 2008)。石块采用Mohr-Coulomb模型，土体采用Cvisc黏弹塑性蠕变模型，蠕变时间为1ia。其Cvisc模型参数如表 2所示。

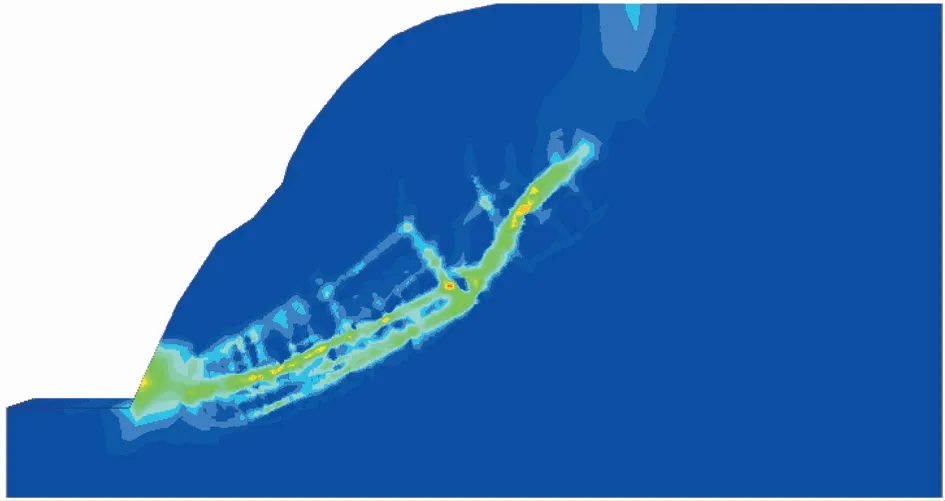
图 7 考虑蠕变效应时边坡剪应变速率云图Fig. 7 Contours of shear strain rate with considering rheology

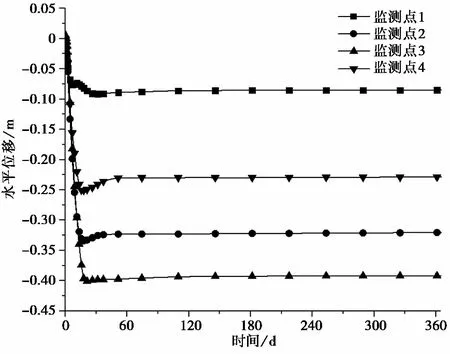
图 8 折减系数为1.46时监测点位移曲线Fig. 8 Horizontal displacement vs time of monitoring points at reduction factor=1.46

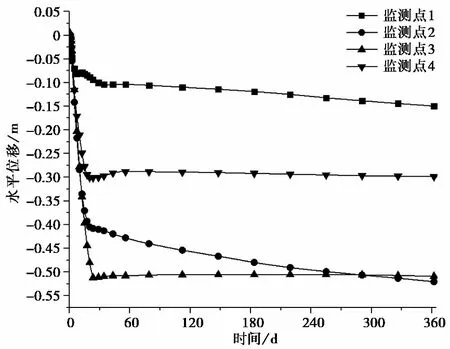
图 9 折减系数为1.47时监测点位移曲线Fig. 9 Horizontal displacement vs time of monitoring points at reduction factor=1.47

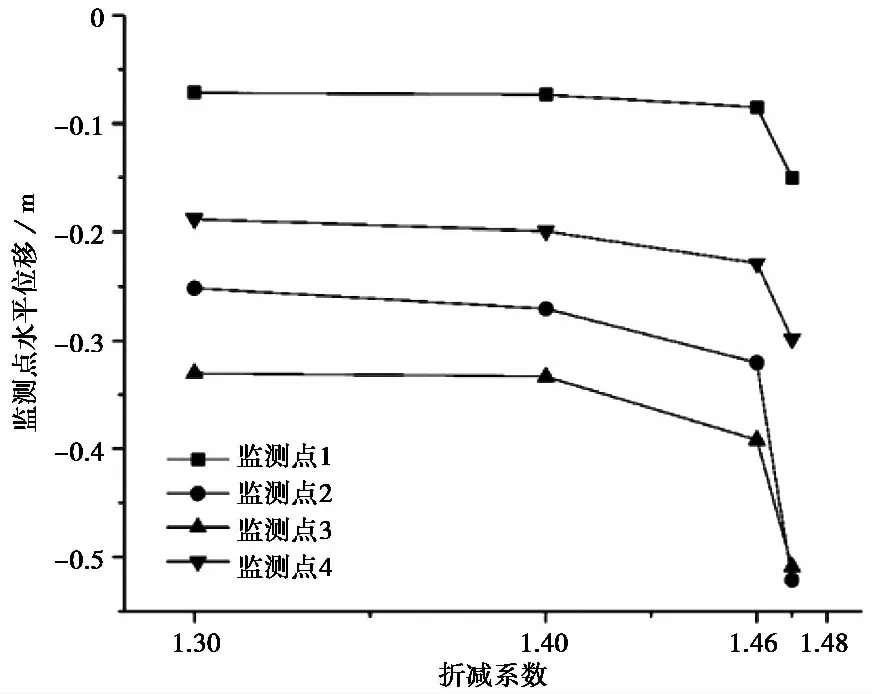
图 10 关键点水平位移与折减系数的关系曲线Fig. 10 Horizontal displacements of monitoring points at different reduction factors with considering rheology

通过自编强度折减法来对考虑蠕变效应的土石混合体边坡进行稳定性分析，其中蠕变参数不变，折减系数从1.30增加到1.47。图 7为折减系数为1.47时的剪应变速率云图，图 8和9为折减系数分别是1.46和1.47时监测点水平位移曲线，可以看到，当折减系数为1.46时，各监测点水平位移在经过短暂的瞬时变形后，位移增加量逐渐减小，最终趋于稳定，位移增加量近似为0。当折减系数增加到1.47时，虽然监测点3和监测点4的位移最终趋于稳定，但监测点1和监测点2在经历1ia的蠕变时间之后，位移仍未收敛。

各关键点水平位移与强度折减系数的关系曲线如图 10所示，可以看出，折减系数由1.30增加到1.46时，关键点总位移并未发生太大变化，而当折减系数增加到1.47后，可以明显地看到位移曲线有一个突变，位移增大较为明显，而此时其蠕变曲线也未到达稳定状态，因此可以认定，考虑蠕变时该土石混合体边坡的安全系数为1.47，比不考虑蠕变时该土石混合体边坡的安全系数下降了20.5%。以监测点2为例，取折减系数为1.46，不考虑土体蠕变效应时，其水平位移仅为0.002im，而考虑土体蠕变效应时，水平位移为0.32im，是不考虑蠕变效应时的160倍，可见土体蠕变对边坡变形影响极大； 在不考虑蠕变效应的情况下取折减系数为1.84，监测点2的水平位移为0.15im，因此若将0.15im作为预测边坡失稳的位移量则显得过于保守。

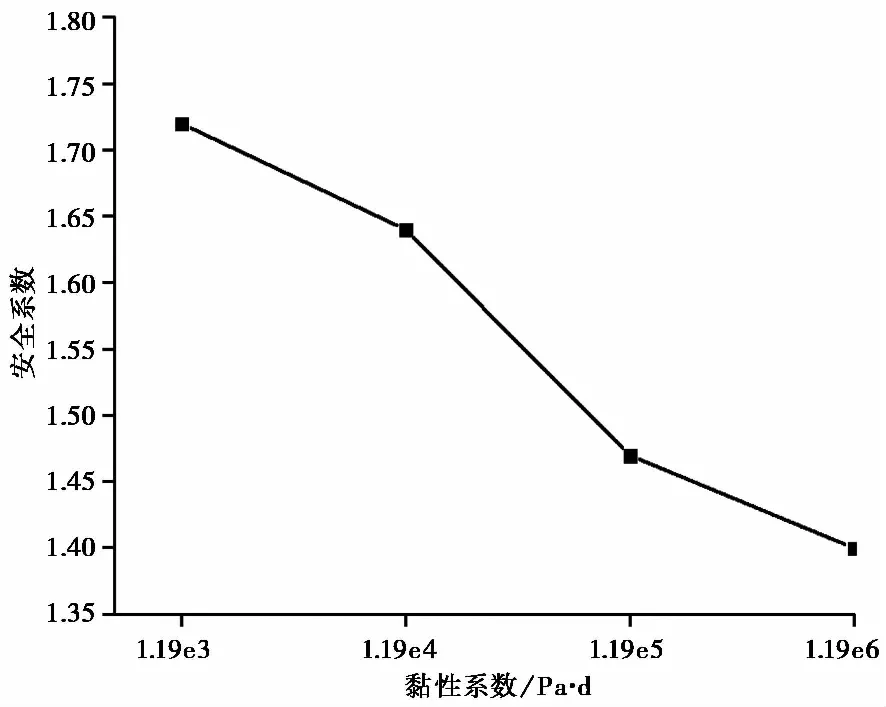
图 11 不同黏性系数时边坡安全系数Fig. 11 FOS with different viscosity coefficient

3.2 蠕变参数对安全系数的影响

岩土体的黏性系数是反映其蠕变程度的一个重要参数，为探索黏性系数对土石混合体边坡安全系数的影响关系，在其他力学参数不变的情况下，分别取Cvisc模型中的Kelvin黏性系数为1.19e3iPa·d、1.19e4iPa·d、1.19e5iPa·d和1.19e6iPa·d，并对边坡进行稳定性分析。图 11为取不同黏性系数时的边坡安全系数关系图，由图可以看出，黏性系数对于边坡的变形及稳定影响较大，随着黏性系数的增大，边坡安全系数随之减小，说明黏性系数的增大对于边坡的变形及稳定具有不利影响。

4 结 论

土石混合体边坡是自然界中广泛存在的一种岩土体边坡，以我国某水电站库区的一个土石混合体边坡为例，首先运用数字图像处理技术对该边坡进行处理，得到土石混合体边坡的细观物理模型，然后在FLAC3D中运用强度折减法对该边坡进行了稳定性分析，并考虑了土体的蠕变性质，与未考虑蠕变性质的土石混合体边坡稳定性分析结果进行比较，得出以下结论：

(1)土石混合体边坡不同于一般均质土体或岩质边坡，在达到临界失稳状态时，在边坡内部会出现多条滑带，且滑带具有明显的“绕石”现象。

(2)不考虑土体蠕变性质的土石混合体边坡的安全系数为1.85，而考虑了土体蠕变性质的土石混合体边坡的安全系数为1.47，相比下降了20.5%； 在取折减系数同为1.46的情况下，考虑土体蠕变效应的边坡监测点水平位移是不考虑蠕变效应时的160倍之多。因此岩土体的蠕变性质不利于边坡的稳定，在对岩土体边坡进行稳定性分析时不应忽略其蠕变性质。

(3)研究了Kelvin黏性系数对边坡进行长期稳定性的影响，认为边坡安全系数随着Kelvin黏性系数的增大而减小，说明黏性系数对于岩土体边坡的变形及稳定具有不利影响。